Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Punkte und Vektoren im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 19: | Zeile 19: | ||
{{Box|1= Aufgabe 1: Koordinatensysteme|2= Für diese Aufgabe benötigst du einen Bleistift, ein kariertes Blatt Papier und ein Geodreieck. Bearbeite die folgenden Aufgaben. | {{Box|1= Aufgabe 1: Koordinatensysteme|2= Für diese Aufgabe benötigst du einen Bleistift, ein kariertes Blatt Papier und ein Geodreieck. Bearbeite die folgenden Aufgaben. | ||
# Zeichne ein dreidimensionales Koordinatensystem. Wähle eine passende Skalierung anhand der angegebenen Punkte im Aufgabenteil 2 und 3. | # Zeichne ein dreidimensionales Koordinatensystem. Wähle eine passende Skalierung anhand der angegebenen Punkte im Aufgabenteil 2 und 3. | ||
# Zeichne die Punkte <math> A (1|2|1)</math>,<math> B(1|4|2)</math>, <math> C(1|2|{-}1,5)</math> und <math> D(1|4|{-}0,5) </math> in das gezeichnete Koordinatensystem. Zeichne nun die Strecken <math>\vec{ AB }</math> , <math>\vec{ AC }</math>,<math>\vec{ CD }</math> und <math>\vec{ BD }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | # Zeichne die Punkte <math> A (1|2|1)</math>,<math> B(1|4|2)</math>, <math> C(1|2|{-}1{,}5)</math> und <math> D(1|4|{-}0{,}5) </math> in das gezeichnete Koordinatensystem. Zeichne nun die Strecken <math>\vec{ AB }</math> , <math>\vec{ AC }</math>,<math>\vec{ CD }</math> und <math>\vec{ BD }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | ||
# Nutze den Punkt <math> A (1|2|1)</math> aus Aufgabenteil 2. Füge die Punkte <math> E (-1|2|1)</math>,<math> F(1|0|1)</math>, <math> G(-1|0|1)</math> und <math> H(0|1|5) </math>. Zeichne nun die Strecken <math>\vec{ AE }</math>,<math>\vec{ AF }</math>, <math>\vec{ AH }</math>, <math>\vec{ EG }</math>, <math>\vec{ AH }</math>, <math>\vec{ FG }</math>, <math>\vec{ FH }</math> und <math>\vec{ GH }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | # Nutze den Punkt <math> A (1|2|1)</math> aus Aufgabenteil 2. Füge die Punkte <math> E (-1|2|1)</math>,<math> F(1|0|1)</math>, <math> G(-1|0|1)</math> und <math> H(0|1|5) </math>. Zeichne nun die Strecken <math>\vec{ AE }</math>,<math>\vec{ AF }</math>, <math>\vec{ AH }</math>, <math>\vec{ EG }</math>, <math>\vec{ AH }</math>, <math>\vec{ FG }</math>, <math>\vec{ FH }</math> und <math>\vec{ GH }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | ||
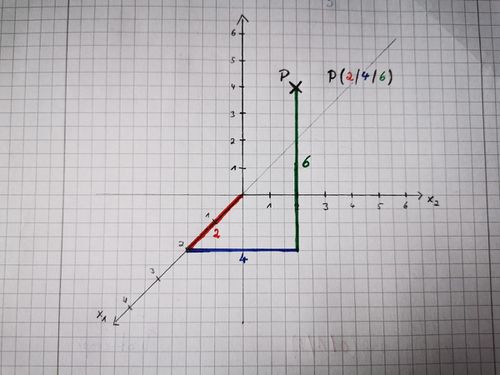
{{Lösung versteckt|1= Punkte in einem dreidimensionalen Koordinatensystem kannst du mithilfe eines "Pfad-Folge-Verfahren" genau bestimmen. Dabei geht man die durch die Punktkoordinaten angegeben Längeneinheiten in die Richtung der jeweiligen Achsen. Das folgende Bild verdeutlicht das Verfahren. | {{Lösung versteckt|1= Punkte in einem dreidimensionalen Koordinatensystem kannst du mithilfe eines "Pfad-Folge-Verfahren" genau bestimmen. Dabei geht man die durch die Punktkoordinaten angegeben Längeneinheiten in die Richtung der jeweiligen Achsen. Es entsteht einen Koordinatenzug. Das folgende Bild verdeutlicht das Verfahren. | ||
[[Datei:Punkte im dreidimensionalen Koordinatensystem.jpg|rahmenlos|500x500px|Pfad-Folge-Verfahren]] |2= Tipp|3=Einklappen}} | [[Datei:Punkte im dreidimensionalen Koordinatensystem.jpg|rahmenlos|500x500px|Pfad-Folge-Verfahren]] |2= Tipp|3=Einklappen}} | ||
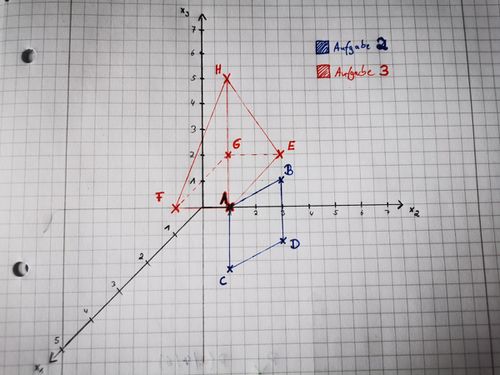
{{Lösung versteckt|1= Bei | {{Lösung versteckt|1= Bei Aufgabenteil 2 handelt es sich um ein Parallelogram. Bei Aufgabenteil 3 bekommst du eine Pyramide heraus, die eine quadratische Grundfläche besitzt. Deine Lösung kann aufgrund einer anderen Skalierung der Achsen natürlich auch von der folgenden Lösung abweichen. | ||
[[Datei:Lösung Aufgabe 1-2-3.jpg|rahmenlos|500x500px|Lösung]] |2= Lösung|3=Einklappen}} | [[Datei:Lösung Aufgabe 1-2-3.jpg|rahmenlos|500x500px|Lösung]] |2= Lösung|3=Einklappen}} | ||
| Zeile 60: | Zeile 60: | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{Wo liegt der Scheitelpunkt der Pyramide ?} | {Wo liegt der Scheitelpunkt der Pyramide ?} | ||
+ Der Scheitelpunkt liegt bei <math> S (2,5|2,5|6) </math>. | + Der Scheitelpunkt liegt bei <math> S (2{,}5|2{,}5|6) </math>. | ||
- Der Scheitelpunkt liegt bei <math> S (5|5|5) </math>. | - Der Scheitelpunkt liegt bei <math> S (5|5|5) </math>. | ||
- Der Scheitelpunkt liegt bei <math> S (2,5|2,5|5) </math>. | - Der Scheitelpunkt liegt bei <math> S (2{,}5|2{,}5|5) </math>. | ||
</quiz> | </quiz> | ||
{{Lösung versteckt|1=Bei der Berechnung des Scheitelpunkts sind die 2 der 3 Koordinaten durch die Bestimmung der Seitenflächen vorgegeben. Dabei solltest du beachten, dass nicht die volle Seitenfläche berechnet wird.|2= Tipp 3|3=Einklappen}} | {{Lösung versteckt|1=Bei der Berechnung des Scheitelpunkts sind die 2 der 3 Koordinaten durch die Bestimmung der Seitenflächen vorgegeben. Dabei solltest du beachten, dass nicht die volle Seitenfläche berechnet wird.|2= Tipp 3|3=Einklappen}} | ||
| Zeile 83: | Zeile 83: | ||
# <math>\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} - \vec{u}-\vec{w}-\vec{v} </math> | # <math>\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} - \vec{u}-\vec{w}-\vec{v} </math> | ||
# <math>\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \vec{v} + \vec{w}+ \vec{u}</math> | # <math>\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \vec{v} + \vec{w}+ \vec{u}</math> | ||
# <math>\begin{pmatrix} 0,5 \\ 2 \\ 1 \end{pmatrix} + \vec{w} + \vec{u} +\vec{v} </math> | # <math>\begin{pmatrix} 0{,}5 \\ 2 \\ 1 \end{pmatrix} + \vec{w} + \vec{u} +\vec{v} </math> | ||
# <math>\begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} + \vec{u} - \vec{w}</math> | # <math>\begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} + \vec{u} - \vec{w}</math> | ||
# <math>\begin{pmatrix} -1 \\ 2 \\ -1\end{pmatrix} + \vec{v} - \vec{v}</math> | # <math>\begin{pmatrix} -1 \\ 2 \\ -1\end{pmatrix} + \vec{v} - \vec{v}</math> | ||
| Zeile 97: | Zeile 97: | ||
# <math>\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} </math> | # <math>\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} </math> | ||
# <math>\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} </math> | # <math>\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} </math> | ||
# <math>\begin{pmatrix} 0,5 \\ 2 \\ 1 \end{pmatrix} </math> | # <math>\begin{pmatrix} 0{,}5 \\ 2 \\ 1 \end{pmatrix} </math> | ||
# <math>\begin{pmatrix} 4 \\ -2 \\ 1 \end{pmatrix} </math> | # <math>\begin{pmatrix} 4 \\ -2 \\ 1 \end{pmatrix} </math> | ||
# <math>\begin{pmatrix} -1 \\ 2 \\ -1 \end{pmatrix} </math> | # <math>\begin{pmatrix} -1 \\ 2 \\ -1 \end{pmatrix} </math> | ||
| Zeile 136: | Zeile 136: | ||
{<math> A(8|9|10) </math> und <math> B(2|6|8) </math>} | {<math> A(8|9|10) </math> und <math> B(2|6|8) </math>} | ||
- <math> 9,5 </math> | - <math> 9{,}5 </math> | ||
+ <math> 7 </math> | + <math> 7 </math> | ||
- <math> 8 </math> | - <math> 8 </math> | ||
- <math> 6,5 </math> | - <math> 6{,}5 </math> | ||
{<math> A(-1|{-}2|2) </math> und <math> B(-3|{-}1|0) </math>} | {<math> A(-1|{-}2|2) </math> und <math> B(-3|{-}1|0) </math>} | ||
| Zeile 179: | Zeile 179: | ||
|2= | |2= | ||
In einem kartesischen Koordinatensystem sind die Punkte <math> A(3|3|5)</math>, <math> B(3,5|3,5|1)</math> und <math> C(6,5|2,5|3) </math> gegeben. | In einem kartesischen Koordinatensystem sind die Punkte <math> A(3|3|5)</math>, <math> B(3{,}5|3{,}5|1)</math> und <math> C(6{,}5|2{,}5|3) </math> gegeben. | ||
<quiz display="simple"> | <quiz display="simple"> | ||
Version vom 29. Mai 2021, 17:28 Uhr
Wiederholung von Punkten und Vektoren