Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Punkte und Vektoren im Raum

Info

In diesem Lernpfadkapitel kannst du etwas über Punkte und Vektoren im Raum lernen und wirst erfahren, was Schrägbilder und Netze von geometrischen Körpern sind und wie du sie zeichnen kannst. Ebenfalls erwartet dich in diesem Kapitel, was unmögliche Figuren sind und woran du diese erkennen kannst. Dir stehen eine Vielzahl an verschiedenen Aufgaben zum Üben zur Verfügung.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.

• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.

• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.

Viel Erfolg!

Wiederholung von Punkten und Vektoren

Erinnerung: Punkte und Vektoren im Raum

Diesdas Lennarts machts

Das dreidimensionale Koordinatensystem

Erinnerung: Bekannte Körper

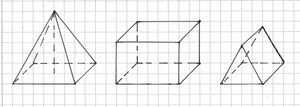
Der Würfel besteht aus sechs gleichgroßen Flächen. Zudem besitzt der Würfel 12 gleichlange Kanten und acht Ecken.

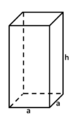
Der Quader besteht aus sechs rechteckigen Seitenflächen, die im rechten Winkel aufeinander stehen. Die gegenüberliegenden Seiten sind jeweils parallel und gleich groß.

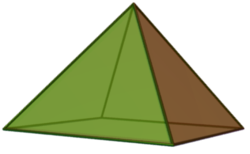
Die Pyramide besitzt eine (4,5,6, ...) - seitige Grundfläche. An jeder Seite der Grundfläche liegt eine dreieckige Seitenfläche an. Die (4,5,6,...) Seitenflächen werden in der Spitze der Pyramide zusammengeführt und Mantelfläche genannt.

Ein Tetraeder ist ein Körper mit vier dreieckigen Seitenflächen. Er wird auch als dreiseitige Pyramide bezeichnet.

Datei:Prisma triangular.png

Ein Prisma besitzt eine Grundfläche und eine gegenüberliegende Deckfläche, welche gleich groß sind. Die Seitenflächen werden zusammen als Mantelfläche bezeichnet. Zudem sind die Seitenkanten, die die Grundfläche und Deckfläche verbinden alle gleichlang und liegen parallel zueinander.

Die beiden Grundflächen eines Zylinders sind kreisförmig, liegen parallel zueinander und sind gleichgroß. Außerdem werden sie durch den Mantel des Zylinders verbunden.

Übung 1: Lückentext Körper

Ziehe die korrekten Wörter in die jeweiligen Lücken.

Im Schrägbild nimmt man Körper auf der ebenen Fläche räumlich wahr.

Die Vorderseite des Quaders solltest du in Originalgröße zeichnen. Wenn der Quader eine Länge von  8 cm und eine Höhe von 2 cm hat, ist das Rechteck, das du als seine Vorderseite zeichnest,  8 cm breit und 2 cm hoch.

Ein Würfel hat 8 Ecken, 6 Flächen und 12 Kanten. Außerdem sind alle Kanten gleich lang und alle Flächen quadratisch. Auch sind die Flächen gleich groß.

Eine Pyramide ist ein Körper, der aus einem Vieleck (Drei-, Vier-, Fünfeck usw.) und mehreren Dreiecken besteht. Das Vieleck bildet die Grundfläche und die Dreiecke die Mantelfläche der Pyramide.

Schau dir die Infobox zu den bekannten Körpern noch einmal an.

Übung 2: Körper in der Realität wiedererkennnen

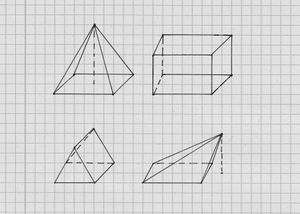
Welche Körper sind gegeben?

Schau dir die Infobox zu den bekannten Körpern noch einmal an.

Schrägbilder und Netze

Erinnerung: Schrägbilder und Körpernetze

Körpernetze und Schrägbilder sind Darstellungshilfen, die man in der Geometrie benutzt. Durch ein Schrägbild wird auf einer ebenen Fläche ein Körper räumlich dargestellt. Beispielsweise kann man einen dreidimensionalen Körper auf einem zweidimensionalen Blatt Papier abbilden.

• Ein Körpernetz entsteht, wenn man den dreidimensionalen Körper an einigen Kanten aufschneiden und dann auseinanderklappen würde.
• Bei einem Schrägbild zeichnest du den Köper, wie der Name schon sagt, schräg von der Seite. Hierbei ist wichtig, dass die schrägen Linien meistens im Winkel von $45$° gezeichnet werden. Je nach Blickpunkt, verändert sich die Perspektive auf den Körper. Die verdeckten Linien, die man von vorne nicht sehen kann, werden gestrichelt dargestellt.

Erinnerung: Wie zeichnet man ein Schrägbild?

Jeder Körper hat eine Grundfläche. Zum Zeichnen von Schrägbildern sollten mehrere Regeln berücksichtigt werden. Zunächst wird die Grundfläche des Körpers in der angegebenen Längeneinheit auf ein Blatt Papier übertragen. Die Längen, die in die Blattebene hinlaufen, werden verkürzt darstellt. Um die Längen zu verkürzen, multipliziert man die reale Länge der Kante mit einem Verkürzungsfaktor $q$. Der Verkürzungsfaktor $q$ beträgt meistens $q= 0{,}5$. Zu beachten ist außerdem, dass die verkürzten Kanten schräg gezeichnet werden. Die Höhe steht immer senkrecht auf der Grundfläche und wird in der angegebenen Längeneinheit gezeichnet.

Beispielkonstruktion eines Quaders:

Übungen: Netze

Übung 1: Würfelnetze

Giovanni, Yasmin und Mehmet haben jeweils das Netz eines Würfels gezeichnet. Beurteile, ob die Körpernetze korrekt gezeichnet wurden.

Stelle dir vor, dass du die Kanten aneinander klebst. Was kannst du ausschließen? Welche Eigenschaften kennst du, die hier nicht zutreffen?

Wer hat richtig gezeichnet?

(Giovanni und Yasmin) (!Alle) (!Yasmin und Mehmet) (!Giovanni und Mehmet)

Übung 2: Kanten kleben

Markiere die Kanten, die die gleiche Kantenlänge haben, in derselben Farbe!

Stell dir am Besten vor, wie du die Seiten des Netzes knicken und verkleben musst, damit der Körper eines Prismas entsteht.

Übung 3: Wahr- und Falschaussagen über Schrägbilder

Bestimme, ob die folgenden Aussagen wahr oder falsch sind.

Wenn ein Quader im Schrägbild dargestellt wird, dann sind die Deck- und die Grundfläche immer gleich groß. (wahr) (!falsch)

Es gibt mehr als eine Lösung für Körpernetze von Schrägbildern. (wahr) (!falsch)

Schrägbilder haben keine versteckten Ecken oder Kanten. (wahr) (!falsch)

Schrägbilder stellen geometrische Figuren auf dem Papier dar. (wahr) (!falsch)

Falls ihr eine Frage falsch beantwortet habt, könnt ihr hier noch einmal die Erklärung zu den Lösungen nachgucken.

1) Bei der Konstruktion eines Quaders werden lediglich die nach hinten verlaufenden Kanten verkürzt dargestellt. Da Deck- und Grundfläche parallel zueinander liegen, sind sie immer gleichgroß.

2) Zu jedem Körper gibt es mehrere Netze. Je nach dem welche Kante aufgeschnitten wird, entsteht ein anderes Netz.

3) Wenn du das Schrägbild korrekt gezeichnet hast, dann solltest du aus verschiedenen Perspektiven immer alle Ecken und Kanten sehen können.

4) Du konstruierst Schrägbilder, um geometrische Figuren bzw. räumliche Körper auf dem Papier darzustellen.

Übung 4: Netze der bekannten Körper

Für die folgende Aufgabe benötigst du einen gespitzten Bleistift, dein Heft und Geodreieck. Zeichne das Netz

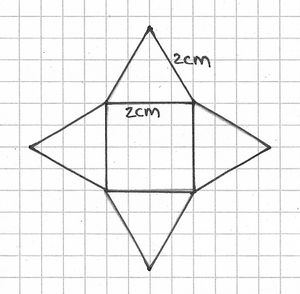
a) einer Pyramide, welche aus vier gleichseitigen Dreiecken mit Seitenlänge $2$ cm und einer quadratischen Grundfläche mit Seitenlänge von $2$ cm besteht.

Beachte die Infobox zu Netzen. Wenn dir das nicht weiter hilft, scrolle ans Ende der Seite.

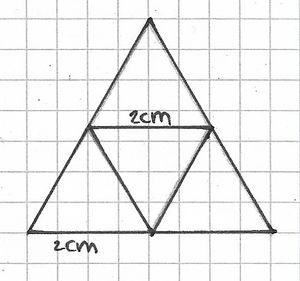
b) eines Tetraeder mit Seitenlänge $2$ cm.

Beachte die Infobox zu Netzen. Wenn dir das nicht weiter hilft, scrolle ans Ende der Seite.

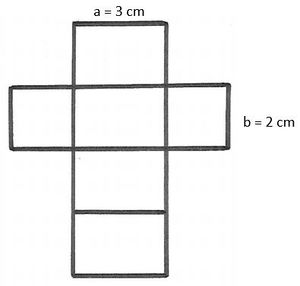
c) eines Quaders, welcher $1$ cm breit, $2$ cm lang und $1$ cm hoch ist.

Beachte die Infobox zu Netzen. Wenn dir das nicht weiter hilft, scrolle ans Ende der Seite.

d) eines dreieckigen Prismas, welches aus zwei gleichseitigen Dreiecken mit Seitenlänge $1$ cm besteht. Die Breite des Prismas soll $2$ cm betragen.

Beachte die Infobox zu Netzen. Wenn dir das nicht weiter hilft, scrolle ans Ende der Seite.

Übung 5: Netze zusammenfalten

Sind die gegebenen Netze die Netze einer Pyramide? Die weiteren Netze erscheinen, wenn du den Regler auf der rechten Seite bewegst.

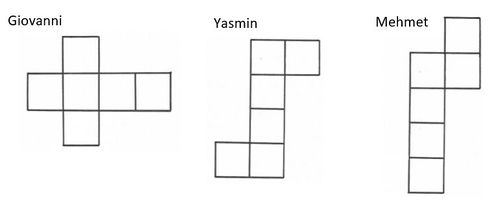
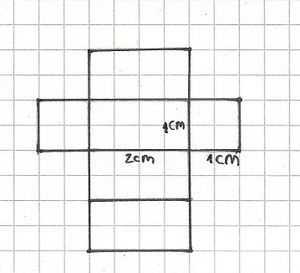
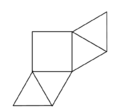
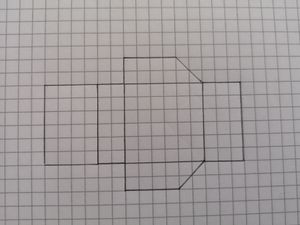
Netz 1 ist das Netz einer Pyramide. (wahr) (!falsch)

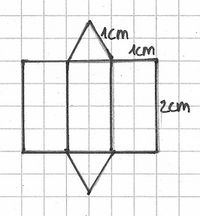
Netz 2 ist das Netz einer Pyramide. (!wahr) (falsch)

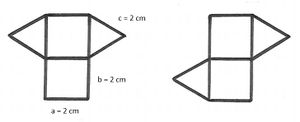
Netz 3 ist das Netz einer Pyramide. (wahr) (!falsch)

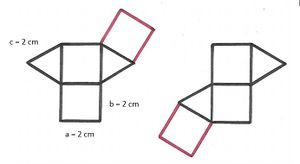
Netz 4 ist das Netz einer Pyramide. (!wahr) (falsch)

Netz 5 ist das Netz einer Pyramide. (!wahr) (falsch)

• Netz 1 ist das Netz einer Pyramide, da alle Seiten der Dreiecke sich treffen, d.h. dass die benachbarten Seiten der Dreiecke jeweils gleich lang sind.
• Netz 2 ist nicht das Netz einer Pyramide, da die längeren Seiten des höheren Dreiecks nicht mit den des weniger hohen Dreiecks übereinstimmen.
• Netz 3 ist das Netz einer Pyramide, da alle Seiten der Dreiecke sich treffen, d.h. dass die benachbarten Seiten der Dreiecke jeweils gleich lang sind.
• Netz 4 ist nicht das Netz einer Pyramide, da die Seiten der Dreiecke sich nicht treffen, wenn man die Dreiecke nach unten versucht zusammenzuklappen, d.h. die benachbarten Seiten der Dreiecke sind jeweils nicht gleich lang.
• Netz 5 ist nicht das Netz einer Pyramide, da die Seiten der Dreiecke sich nicht treffen, d.h. dass die benachbarten Seiten der Dreiecke jeweils nicht gleich lang sind.

Übung 6: Netze von Prismen

Zeichne die folgenden Netze in dein Heft und ergänze fehlende Flächen, damit das Netz eines Prismas entsteht.

Schau dir zunächst noch einmal an, wie ein Prisma aussieht und welche Flächen es hat. Dann überlege dir, welche Flächen in den gegebenen Netzen fehlen könnten.

Vergleiche die angegebenen Lösungen mit deinen eigenen Netzen. Bei dieser Aufgabe solltest du beachten, dass die angegebenen Lösungen nur mögliche Lösungen sind.

Übungen: Schrägbilder

Übung 1: Memory

Gegeben sind Körpernetze und Schrägbilder. Finde die passenden Paare.

Quadratische Pyramide
120px-Hexahedron-slowturn	Hexahedron flat color
120px-Tetrahedron-slowturn	Tetrahedron flat
Quader mit Raumdiagonale d	Auseinander geklapptes Netz eines Quaders
dreieckiges Prisma

• Falls du nicht mehr weißt, wie die Schrägbilder der bekannten Körper aussehen, dann guck noch einmal in der Erinnerungsbox zu den bekannten Körpern nach.
• Falls du nicht mehr weißt, wie die Netze der bekannten Körper aussehen, dann guck noch einmal hier nach: Das Netz eines Quaders, dreieckigen Prismas, einer Pyramide und eines Tetraeders findest du in den Lösungen von Aufgabe "nach Konstruktion zeichnen". Das Netz eines Würfels siehst du, wenn du Aufgabe 1 zu Schrägbildern richtig gelöst hast.

Übung 2: Schrägbild zeichnen

Wie sieht das Schrägbild des folgenden Körpernetzes aus? Zeichne die Lösung in dein Heft und überprüfe dein Ergebnis mit der angegebenen Lösung.

Falls du keine Idee hast, um welchen Körper es sich hier handeln könnte, schau dir oben noch einmal die Erinnerung der bekannten Körper an.

Wenn du das Netz einem Körper zu ordnen konntest, dann überlege dir welche Seiten zu einander parallel sind.

Das angegebene Netz ist das Netz eines Quaders. Jetzt solltest du es mit den angegebenen Längeneinheiten zeichnen können.

Vergleiche die angegebene Lösung mit deiner Lösung im Heft.

Übung 3: Zeichnung eines Netzes

Zeichne das Netz des folgenden Schrägbildes und benutze die angegebenen Längen. Zeichne das Netz in dein Heft.

Fange mit der größten quadratischen Grundfläche an, und überlege, wie du von hieraus ein Netz formen kannst.

Welche Kanten des Körper musst du ,,einschneiden" um das Netz zu formen? Überlege dir, was passiert, wenn du einige Kanten ,,einschneidest". Entsteht so dein Körpernetz?

,,Schneide" alle Kanten ein, die senkrecht von der quadratischen Grundfläche hochführen. Trenne nun die nicht-rechteckigen Seitenflächen der Grundfläche von der gegenüberliegenden Fläche der Grundfläche. Nun muss nur noch eine Kante ,,eingeschnitten" werden, um das Körpernetz zu erhalten.

So sieht eine mögliche Lösung des Körpernetztes des gegebenen Schrägbildes aus. Die Seiten, die senkrecht der Grundfläche hochgehen, wurden ,,eingeschnitten". Danach wurden die anliegenden nicht-rechteckigen Seiten der Grundfläche von der gegenüberliegenden Fläche der Grundfläche getrennt. Als letztes wurde eine rechteckige Seitenfläche der Grundfläche von der gegenüberliegenden Fläche der Grundfläche getrennt.

Übung 4: Schrägbilder korrigieren

Sofia hat im Unterricht das Schrägbild eines dreieckigen Prismas und eines Quaders, sowie Schrägbilder zweier Pyramiden gezeichnet. Beurteile, ob die Schrägbilder richtig sind. Falls sie falsch sind, finde die Fehler und korrigiere die Schrägbilder.

• 
  Figur 1: Die versteckten Linien wurden nicht gestrichelt gezeichnet.
• 
  Figur 2: Hier liegt der Fehler darin, dass die markierten Längen, die in die Blattebene hinlaufen, auf der linken Seite des Quaders nicht denselben Winkel haben wie die anderen beiden, die in die Blattebene laufen, auf der rechten Seite. (Hier hättest du genauso gut die anderen beiden Längen, die in Blattebene hineinlaufen, auf der rechten Seite als Fehler markieren können.) Weiterhin wurde die hintere versteckte Linien nicht gestrichelt gezeichnet.
• 
  Figur 3: Hier sehen wir, dass die markierte Länge, die in die Blattebene hinlaufen, nicht denselben Winkel haben wie die anderen beiden, die in die Blattebene laufen. Somit verändert sich auch die eine Seite des hinteren Dreiecks.
• Figur 4 wurde richtig gezeichnet.

Übung 5: Zeichnen und Messen - Quader

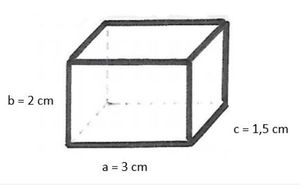
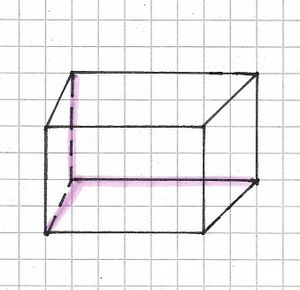
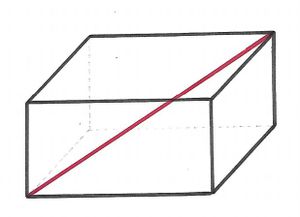
Ein Quader hat eine Länge von $8$ cm, eine Breite von $8$ cm und eine Höhe von $4$ cm. Zeichne sein Schrägbild in dein Heft und miss mit dem Lineal nach, wie weit die Ecke unten links vorn von der Ecke oben rechts hinten entfernt ist.

Die gesuchte Strecke ist ($12{,}8$ cm lang.) (!$10{,}1$ cm lang.) (!$14{,}3$ cm lang.) (!$8{,}6$ cm lang.)

Zunächst zeichnest du in wahrer Länge die Vorderseite des Quaders. Das Rechteck hat dann eine Länge von $8$ cm und eine Höhe von $4$ cm.

Im zweiten Schritt zeichnest du von den vier Eckpunkten jeweils eine Hilfsgerade im Neigungswinkel $45$°.

Jetzt multiplizierst du die angegebene Breite mit dem Verkürzungsfaktor $q = 0{,}5$. Die errechnete Kantenlänge von $4$ cm soll jetzt die Länge der Hilfsgeraden darstellen. Hier passt du deine anfänglich gezeichneten Hilfsgeraden an die Länge von $4$ cm an.

Die neu konstruierten Punkte verbindest du abschließend noch miteinander und zeichnest die nicht sichtbaren Linien gestrichelt ein.

Die gesuchte Strecke beträgt $12{,}8$ cm.

Übung 6: Zeichnen und Messen - Prisma

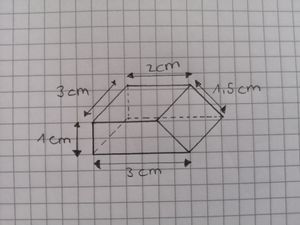
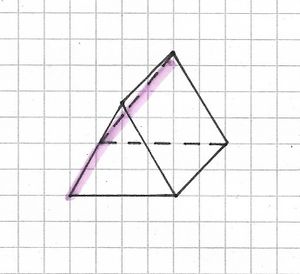
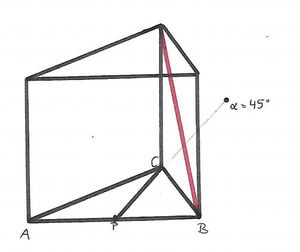
Ein gleichseitiges Prisma hat eine Seitenlänge von $a=6$ cm und eine Höhe von $h=5$ cm. Zeichne das Schrägbild in dein Heft und miss mit dem Lineal nach, wie weit die vordere Ecke unten rechts von der hinteren Ecke oben entfernt ist.

Die gesuchte Strecke ist ($6{,}9$ cm lang.) (!$5{,}3$ cm lang.) (!$7{,}4$ cm lang.) (!$5{,}8$ cm lang.)

Zunächst zeichnest du die Strecke $AB=6$ cm in wahrer Länge.

Da es sich bei dem Körper um ein gleichseitiges Prisma handelt, schneidet die Höhe die Strecke $AB$ genau im Mittelpunkt $P$. Von diesem Punkt $P$ ziehst du nun in einem Winkel von $45$° eine Hilfslinie. Um die Länge der Hilfslinie zu ermitteln, multiplizierst du die angegebene Höhe mit $0{,}5$ . Hier hätte die Strecke dann eine Länge von $2{,}5$ cm.

Jetzt verbindest du den entstandenen Punkt $C$ mit den Punkten $A$ und $B$, um die Grundfläche des Prismas zu erhalten.

Nun zeichnest du jeweils von den Punkten $A, B$, und $C$ eine senkrechte Linie, die der Höhe von $5$ cm entspricht. Um die Konstruktion abzuschließen, verbindest du die weiteren Eckpunkte miteinander.

Die gesuchte Strecke beträgt $6{,}9$ cm.

Übung 7: nach Konstruktionsbeschreibung zeichnen

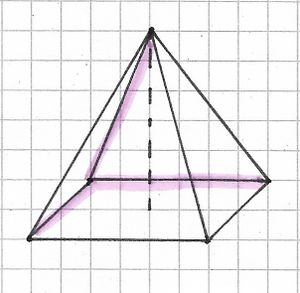
Für diese Aufgabe benötigst du einen gespitzten Bleistift, Heft und Geodreieck. Zeichne eine Pyramide mithilfe folgender Konstruktionsbeschreibung. Die Kantenlängen kannst du frei wählen.

Schritt 1: Die quadratische Grundfläche der Pyramide wird als Parallelogramm $ABCD$ gezeichnet. Dabei werden die nach hinten verlaufenden Kanten im Winkel von $45$° gezeichnet und in ihrer Länge halbiert.

Schritt 2: Die Spitze $S$ der Pyramide wird senkrecht über dem Mittelpunkt der Grundfläche $ABCD$ angenommen.

Schritt 3: Die Spitze $S$ der Pyramide wird mit den Eckpunkten $A$, $B$, $C$ und $D$ der Grundfläche verbunden. Sichtbare Linien werden durchgezeichnet. Nicht sichtbare Linien werden punktiert.

Weil die Lösung nicht in dieser Box angezeigt werden kann, scrolle ganz ans Ende der Seite, um die Lösung zu sehen.

Unmögliche Figuren

Unmögliche Figuren

Falls du dir unsicher bist, was unmögliche Figuren sind, lies dir die Infobox einmal durch.

Unmögliche Figuren sind grafisch zweidimensionale Figuren, die dreidimensional erscheinen aber als Körper in der Realität nicht existieren können. Die geometrischen, dreidimensionalen Objekte kann man in der Realität gar nicht herstellen. Gezeichnet werden können sie auf (dem zweidimensionalen) Papier aber ohne Probleme. Bei den Figuren handelt es sich meist um optische Täuschungen.

Beispiele von unmöglichen Figuren:

Die unmögliche Lattenkiste

Unmöglicher Würfel

Idee

Vielleicht kennst du ja auch schon ein paar unmögliche Figuren, natürlich nicht aus unserer Realität, aber ja aus Filmen? Eine der obigen Figuren kommt zum Beispiel in einer Szene aus Inception (2010) vor, die du dir hier auf YouTube angucken kannst:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übungen: unmögliche Figuren

Übung 1: Erkennst du die unmöglichen Figuren?

Im unteren Kasten siehst du unmögliche Figuren und nicht unmögliche Figuren. Bestimme, ob die Figuren unmöglich sind oder nicht. Ziehe dafür das Bild in den zugehörigen Kasten.

unmögliche Figuren
geometrische Körper/Konstruktionen

Übung 2: Aus unmöglich mach möglich!

Wie müsste man den unmöglichen Würfel verändern, damit diese/r keine unmögliche Figur mehr ist?

Unmöglicher Würfel

Man müsste die hinteren Seitenkannten des Würfels zerschneiden, um die vorderen an dieser Stelle sichtbar zu machen. Einen echten, nicht unmöglichen Würfel siehst du hier:

Übung 3: Das Penrose-Dreieck

Betrachte das sogenannte Penrose-Dreieck. Welche Besonderheiten fallen dir auf? Wordurch wird die optische Täuschung hervorgerufen? Welches mathematische Gesetz zeigt, dass das Dreieck im Dreidimensionalen nicht existieren kann? Beantworte im Heft.

In welchem Winkel stehen die Seiten des Dreiecks aufeinander?

Was ist die Winkelsumme eines "möglichen" Dreiecks?

Das Penrose-Dreieck hat drei Seiten, die jeweils im rechten Winkel zueinander stehen und dennoch zu einem Dreieck verbunden sind. Damit verstößt es gegen mehrere mathematische Gesetze der Geometrie. Zum Beispiel beträgt die Winkelsumme in einem Dreieck immer $180$°.

Quellen

• https://learnattack.de/mathematik/koerpernetz-und-schraegbild-von-koerpern#video-was-sind-schr%C3%A4gbild-und-netz-eines-k%C3%B6rpers
• https://www.geogebra.org/m/a7wZdw5C#material/Qf9yn4sG
• https://www.geogebra.org/m/SQm8Xq3y
• https://www.geogebra.org/m/ab93zf9g
• https://www.geogebra.org/m/nc7KHTJt
• https://www.geogebra.org/material/show/id/ab93zf9g#
• https://www.geogebra.org/material/show/id/Z57aCNpm#
• https://www.youtube.com/watch?v=dvSD1EAlAUQ
• https://www.klippert-medien.de/media/ntx/klippert/sample/09108DA5_Musterseite.pdf
• https://nl.wikipedia.org/wiki/Onmogelijke_figuur#/media/Bestand:Blivet.png
• https://de.wikipedia.org/wiki/Unm%C3%B6gliche_Figur#/media/Datei:Impossible_staircase.svg
• https://de.wikipedia.org/wiki/Penrose-Dreieck#/media/Datei:Deutsches_Technikmuseum_Berlin_February_2008_0005.JPG
• https://es.wikipedia.org/wiki/Objeto_imposible#/media/Archivo:Reutersv%C3%A4rd%E2%80%99s_triangle.svg
• https://es.wikipedia.org/wiki/Objeto_imposible#/media/Archivo:Impossible_cube_illusion_angle.svg

Geogebra Applets

Pyramidenaufgabe Übung 6 Lösung

Netzaufgabe Übung 4 a Tipp

Netzaufgabe Übung 4 b Tipp

Netzaufgabe Übung 4 c Tipp

Netzaufgabe Übung 4 d Tipp

Aufgabe 8 - Länge und Abstand von Vektoren

{Berechene die Länge der Vektoren.}

a) $\vec{v} = \begin{pmatrix} 12 \\ 3 \\ 4 \end{pmatrix}$ - 12 + 13 - 14 - 15