Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 28: | Zeile 28: | ||
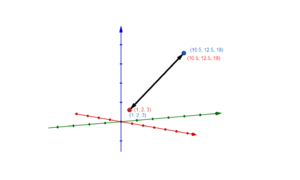
{{Box|1= Aufgabe 1: Geradengleichung aufstellen|2=Die Gerade <math>g</math> geht durch die Punkte <math>A</math> und <math>B</math>. Gib zwei Gleichungen für <math>g</math> an. | {{Box|1= Aufgabe 1: Geradengleichung aufstellen|2=Die Gerade <math>g</math> geht durch die Punkte <math>A</math> und <math>B</math>. Gib zwei Gleichungen für <math>g</math> an. | ||
'''a)''' | '''a)'''<math>A(1|2|2)</math>, <math>B(5|{-}4|7)</math> | ||
'''b)''' | |||
'''c)''' | '''b)'''<math>A(-3|{-}2|9)</math>, <math>B(0|0|3)</math> | ||
'''c)'''<math>A(7|{-}2|7)</math>, <math>B(1|1|1)</math> | |||
''Anmerkung zu den Lösungen: Wie du wahrscheinlich im obigen Video mitbekommen hast, gibt es unendlich viele Lösungen. Daher sind auch Vielfache der Richtungsvektoren oder andere Stützvektoren, wenn sie auf der Geraden <math>g</math> liegen, möglich.'' | |||
{{Lösung versteckt|1=Zwei mögliche Geraden sind <math>g: \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 22 \end{pmatrix} + s \cdot \begin{pmatrix} 4 \\ -6 \\ 5 \end{pmatrix}, s \in \mathbb{R} </math> und <math>g: \vec{x} = \begin{pmatrix} 5 \\ -4 \\ 7 \end{pmatrix} + t \cdot \begin{pmatrix} -4 \\ 6 \\ -5 \end{pmatrix}, t \in \mathbb{R} </math>. | |||
|2=Lösung Aufgabe a) anzeigen|3=Lösung Aufgabe a} verbergen}} | |||
{{Lösung versteckt|1=Zwei mögliche Geraden sind <math>g: \vec{x} = \begin{pmatrix} -3 \\ -3 \\ 9 \end{pmatrix} + s \cdot \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix}, s \in \mathbb{R} </math> und <math>g: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} -3 \\ -2 \\ 6 \end{pmatrix}, t \in \mathbb{R} </math>. | |||
|2=Lösung Aufgabe b) anzeigen|3=Lösung Aufgabe b} verbergen}} | |||
{{Lösung versteckt|1=Zwei mögliche Geraden sind <math>g: \vec{x} = \begin{pmatrix} 7 \\ -2 \\ 7 \end{pmatrix} + s \cdot \begin{pmatrix} -6 \\ 3 \\ -6 \end{pmatrix}, s \in \mathbb{R} </math> und <math>g: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + t \cdot \begin{pmatrix} 6 \\ -3 \\ 6 \end{pmatrix}, t \in \mathbb{R} </math>. | |||
|2=Lösung Aufgabe c) anzeigen|3=Lösung Aufgabe c} verbergen}} | |||
|Farbe={{Farbe|orange}}|3= Hervorhebung1}} | |Farbe={{Farbe|orange}}|3= Hervorhebung1}} | ||
Version vom 25. April 2021, 13:18 Uhr
Geraden und ihre Darstellungsformen
Parameterdarstellung einer Geraden
Wie du nun eine Parametergleichung durch zwei gegebene Punkte, z.B. und , aufstellst, wird im folgenden Video erklärt:
Punktprobe
Spurpunkte einer Geraden
Strecken
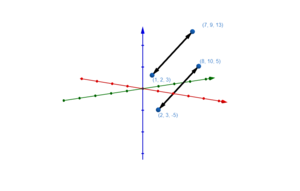
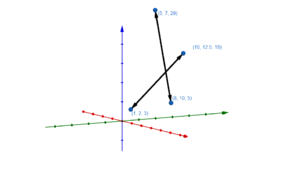
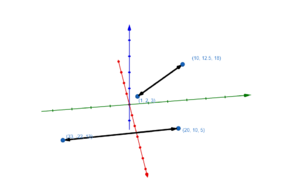
Graphische Darstellung von Geraden im Raum
Lagebeziehungen von Geraden