Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisumfang: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 24: | Zeile 24: | ||
Dieses Verhältnis wird '''Kreiszahl π''' genannt. <math>\tfrac{u}{d}</math> = π. | Dieses Verhältnis wird '''Kreiszahl π''' genannt. <math>\tfrac{u}{d}</math> = π. | ||
|2=Vergleiche deine Lösung|3=Verbergen}} | |2=Vergleiche deine Lösung|3=Verbergen}} | ||
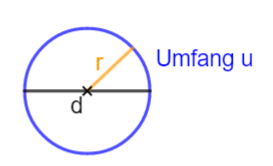
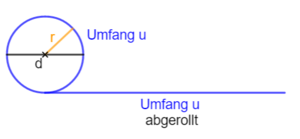
{{Box|1=Kreisumfang| Den '''<u>Umfang u</u>''' eines Kreises mit Durchmesser d (Radius r) berechnen wir mit der Formel:<br> | {{Box|1=Kreisumfang|2=[[Datei:Kreisumfang 1.png|rechts|rahmenlos]][[Datei:Kreisumfang 2.png|rechts|rahmenlos]]Den '''<u>Umfang u</u>''' eines Kreises mit Durchmesser d (Radius r) berechnen wir mit der Formel:<br> | ||
u = π · d oder u = 2· π · r (denn d = 2·r)| | u = π · d oder u = 2· π · r (denn d = 2·r)|3=ARbeitsmethode}} | ||
Version vom 7. April 2021, 06:25 Uhr
SEITE IM AUFBAU!!
1 Kreisumfang
Prüfe deine Vermutung aus dem Teil c) mithilfe des nachfolgenden Applets. Wähle den Vollbildmodus zur Bearbeitung.
Applet von Pöchtrager
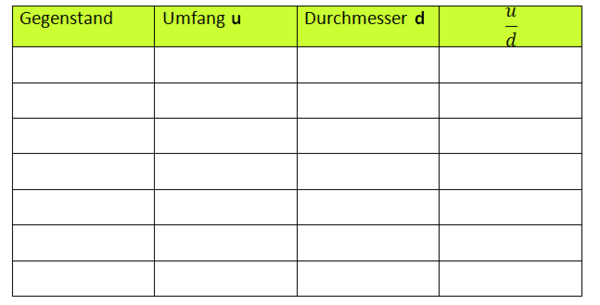
Stelle deine Werte aus der Tabelle in einem d-u-Diagramm dar. Was fällt dir auf?
Das Diagramm ist eine Ursprungsgerade, also ist die Zuordnung proportional. Das heißt auch, dass der Quotient immer gleich ist.
Der Umfang u eines Kreises ist proportional zu seinem Durchmesser d.
Der Quotient beträgt immer ca. 3,1.