Benutzer:Buss-Haskert/Pythagoras/Satz des Pythagoras

SEITE IM AUFBAU!

2 Satz des Pythagoras

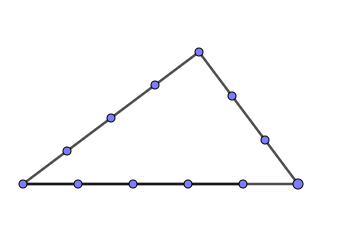
2.1 12-Knoten-Seil

12-Knoten-Seil

Schon im alten Ägypten (lange vor Pythagoras9), gab es Seilspanner, die mithilfe eines 12-Knoten-Seils Felder rechtwinklig einteilen konnten.
Probiere es aus: Teile ein Seil in 12 gleich lange Teile und mache jeweils einen Knoten bzw. markiere die Stelle des Seils farbig. Spanne nun das Seil so, dass du 5 Teile unten (Hypotenuse) und jeweils 3 bzw. 4 Teile an den Seiten (Katheten) hast.
Was beobachtest du?

Prüfe deine Beobachtung mithilfe des nachfolgenden Applets.

Applet von Pöchtrager

Was hat das mit dem Satz des Pythagoras zu tun?

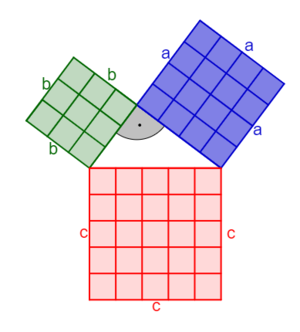
2.2 Satz des Pythagoras

Applet von Pöchtrager

Satz des Pythagoras

In jedem rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse genauso groß wie die Summe der Quadrate über den Katheten.
Für ein rechtwinkliges Dreieck mit dem rechten Winkel γ (γ=90°) heißt der Satz des Pythagoras

a² + b² = c².

Überprüfe die Aussage des Satzes von Pythagoras mithilfe des nachfolgenden Applets.

Applet von Pöchtrager

Zerlegungsbeweise

Es gibt viele Möglichkeiten, den Satz des Pythagoras zu beweisen. Die nachfolgenden GeoGebra-Applets nutzen die Zerlegungsmethode, d.h. die Quadrate über den Katheten werden so zerlegt, dass sie neu zusammengelegt das Hypotenusenquadrat ergeben. Erkläre jeweils!

Beweis Nr. 1:

Applet von J. Mil
Beweis Nr. 2:

Applet von B.Lachner
Beweis Nr. 3:

Applet von Pöchtrager
Beweis Nr. 4:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Auch im Lied von Dorfuchs findest du einen Beweis für den Satz des Pythagoras:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 1 - online

Löse auf der Seite Aufgabenfuchs die Aufgaben

• 1
• 2
• 3
• 4
• 5

Danach bearbeite die Übungen der LearningApp.

Übung 2

Löse die Aufgaben aus dem Buch. Übertrage die Skizze in dein Heft, markiere die Hypotenuse rot und formuliere den Satz des Pythagoras. (Achte darauf, dass deine Skizze ein rechtwinkliges Dreieck ist.)

• S. 111 Nr. 2
• S. 111 Nr. 3

In Nr. 3 gibt es jeweils 3 rechtwinklige Dreiecke pro Figur, das große gesamte Dreieck mit den Katheten x und y und der Hypotenuse (z+w) und die zwei kleinen Dreiecke mit jeweils der Seite y als Kathete.

2.3 Fehlende Seitenlängen in rechtwinkligen Dreiecken berechnen mit dem Satz des Pythagoras

Fehlende Seitenlängen berechnen

Mithilfe des Satzes von Pythagoras lassen sich in rechtwinkligen Dreiecken fehlende Seitenlängen berechnen. Übertrage die Beispiele in dein Heft

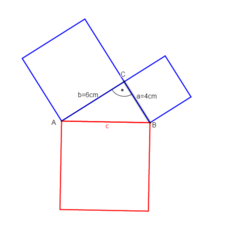
Beispiel 1: Die Katheten sind gegeben und die Hypotenuse ist gesucht.

geg: rechtwinkliges Dreieck mit γ=90°;   Katheten: a = 4cm; b = 6cm

ges: Hypotenuse c

c² = a² + b²   |$\surd$
c = $\sqrt{\text{a² + b²}}$   |Werte einsetzen
c = $\sqrt{\text{4² + 6²}}$   |berechnen
(c = $\sqrt{52}$   diesen Schritt musst du nicht notieren)
c $\approx$7,2 [cm]

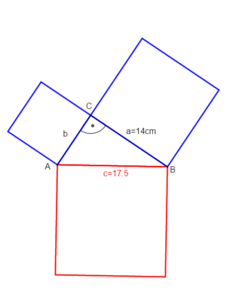
Beispiel 2: Die Hypotenuse und eine Kathete sind gegeben und die andere Kathete ist gesucht.

geg: rechtwinkliges Dreieck mit γ=90°;   Kathete: a = 14cm; Hypotenuse c = 17,5cm

ges: Kathete b

a² + b² = c²   |-a² b² = c² - a²   |$\surd$
b = $\sqrt{\text{c² - a²}}$   |Werte einsetzen
b = $\sqrt{\text{17,5² - 14²}}$   |berechnen
(b = $\sqrt{110,25}$   diesen Schritt musst du nicht notieren)
b = 10,5 [cm]

Hinweis zum Runden: Runde auf so viele Nachkommastellen, wie die Werte in der Aufgabenstellung haben.

Übung 3 - online

Löse auf der Seite Aufgabenfuchs die Aufgaben

• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13

Danach bearbeite die Aufgaben in den GeoGebra-Applets.

Übungen (GeoGebra-Applets von Pöchtrager)

Übung 4

Löse die Aufgaben aus dem Buch. Gehe dabei schrittweise vor:
1. Schritt: Prüfe, dass das Dreieck rechtwinklig ist.
2. Schritt: Entscheide, welche Seiten die Katheten und welche Seite die Hypotenuse ist.
3. Schritt: Notiere im Heft geg:... und ges:... wie in den Beispielen oben.
4. Schritt: Berechne dann wie in den Beispielen oben. Notiere vollständig und runde richtig.

• S. 111 Nr. 4
• S. 111 Nr. 5
• S. 111 Nr. 6 (mit Skizze!)
• S. 111 Nr. 7 (mit Skizze!)

In Aufgabenteil a) ist eine Kathete 4cm lang, von der anderen Kathete kennst du nur das Quadrat (20cm²). Gesucht ist die Hypotenuse x.
x² = 4² + 20   (20 ist schon das Quadrat der zweiten Kathete)
x = $\sqrt{\text{16 + 20}}$

x = 6 [cm]

In Aufgabenteil c) sind die Katheten gleich lang, das Quadrat der Hypotenuse ist gegeben.
50 = x² + x²
50 = 2x²   |:2
25 = x²

...

Um x zu berechnen, teile das Deieck in zwei rechtwinklige Teildreiecke ein (wie in der Skizze gegeben) und berechne die einzelnen Teilstrecken x₁ und x₂. x = x₁ + x₂

Pythagorasbaum: (Appelt von Pöchtrager)