Benutzer:Buss-Haskert/Pythagoras/Satz des Pythagoras: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
SEITE IM AUFBAU! | SEITE IM AUFBAU! | ||
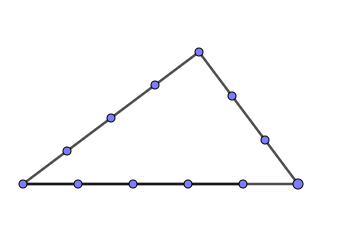
Schon im alten Ägypten (lange vor Pythagoras9), gab es Seilspanner, die mithilfe eines 12-Knoten-Seils Felder rechtwinklig einteilen konnten. | {{Box|12-Knoten-Seil|Schon im alten Ägypten (lange vor Pythagoras9), gab es Seilspanner, die mithilfe eines 12-Knoten-Seils Felder rechtwinklig einteilen konnten. <br> | ||
Probiere es aus: Teile ein Seil in 12 gleich lange Teile und mache jeweils einen Knoten bzw. markiere die Stelle des Seils farbig. Spanne nun das Seil so, dass du 5 Teile unten (Hypotenuse) und jeweils 3 bzw. 4 Teile an den Seiten (Katheten) hast. | |||
Probiere es aus: Teile ein Seil in 12 gleich lange Teile und mache jeweils einen Knoten bzw. markiere die Stelle des Seils farbig. | <br> | ||
Was beobachtest du?<br> | |||
Was beobachtest du? | [[Datei:12 Knoten Seil.png|rahmenlos|347x347px]]|Frage}} | ||
Prüfe deine Beobachtung mithilfe des nachfolgenden Applets. | |||
[[Datei:12 Knoten Seil.png|rahmenlos|347x347px]] | |||
<br /> | <br /> | ||
<ggb_applet id="xmKsCyBc" width="900" height="550" border="888888" /> | <ggb_applet id="xmKsCyBc" width="900" height="550" border="888888" /> | ||
<small>Applet von Pöchtrager</small> | <small>Applet von Pöchtrager</small> | ||
<br> | <br> | ||
Was hat das mit dem Satz des Pythagoras zu tun? | <big>Was hat das mit dem Satz des Pythagoras zu tun</big>? | ||
<br> | <br> | ||
<ggb_applet id="AgezqDax" width="900" height="550" border="888888" /> | <ggb_applet id="AgezqDax" width="900" height="550" border="888888" /> | ||
<small>Applet von Pöchtrager</small> | <small>Applet von Pöchtrager</small> | ||
<br> | <br> | ||
{{Box|Satz des Pythagoras|In jedem rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse genauso groß wie die Summe der Quadrat über den Katheten.<br> | |||
Für ein rechtwinkliges Dreieck mit dem rechten Winkel γ (γ=90°) heißt der Satz des Pythagoras<br> | |||
a² + b² = c². | |||
<ggb_applet id="j3UksqZs" width="900" height="550" border="888888" /> | <ggb_applet id="j3UksqZs" width="900" height="550" border="888888" /> | ||
<small>Applet von Pöchtrager</small> | <small>Applet von Pöchtrager</small> | ||
Version vom 21. Januar 2021, 13:44 Uhr
SEITE IM AUFBAU!
Prüfe deine Beobachtung mithilfe des nachfolgenden Applets.

Applet von Pöchtrager
Was hat das mit dem Satz des Pythagoras zu tun?

Applet von Pöchtrager
{{Box|Satz des Pythagoras|In jedem rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse genauso groß wie die Summe der Quadrat über den Katheten.
Für ein rechtwinkliges Dreieck mit dem rechten Winkel γ (γ=90°) heißt der Satz des Pythagoras
a² + b² = c².

Applet von Pöchtrager
Zerlegungsbeweise:

Applet von J. Mil

Applet von B.Lachner

Applet von Pöchtrager
Übungen (GeoGebra-Applets von Pöchtrager)



Pythagorasbaum:
(Appelt von Pöchtrager)