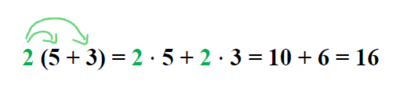Digitale Werkzeuge in der Schule/Fit für VERA-8/Terme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 302: | Zeile 302: | ||
|2=Tipp|3=Verbergen}} <br /> | |2=Tipp|3=Verbergen}} <br /> | ||
b) '''15()''' <math> \cdot x + 35 = 5 \cdot (3x + 7) </math> <br /> | b) '''15()''' <math> \cdot x + 35 = 5 \cdot (3x + 7) </math> <br /> | ||
{{Lösung versteckt|1=Schaue bei Teilaufgabe (i) nach, was du ausklammerst. | |||
|2=Tipp|3=Verbergen}} <br /> | |||
c) <math> 4 \cdot (-3z + 2) = </math> '''-12()''' <math> \cdot z + 8 </math> <br /> | c) <math> 4 \cdot (-3z + 2) = </math> '''-12()''' <math> \cdot z + 8 </math> <br /> | ||
{{Lösung versteckt|1=Schaue bei Teilaufgabe (i) nach, was du ausklammerst. | |||
|2=Tipp|3=Verbergen}} <br /> | |||
d) <math> 9y - 15 = 3 \cdot (3y </math> '''-5()''' <math>)</math> <br /> | d) <math> 9y - 15 = 3 \cdot (3y </math> '''-5()''' <math>)</math> <br /> | ||
{{Lösung versteckt|1=Schaue bei Teilaufgabe (i) nach, was du ausklammerst. | |||
|2=Tipp|3=Verbergen}} <br /> | |||
e) <math> (-24a + 42) \cdot \frac{1}{6} = </math> '''-4()''' <math> \cdot a + </math> '''7()''' | e) <math> (-24a + 42) \cdot \frac{1}{6} = </math> '''-4()''' <math> \cdot a + </math> '''7()''' | ||
{{Lösung versteckt|1=Schaue bei Teilaufgabe (i) nach, was du ausklammerst. | |||
|2=Tipp|3=Verbergen}} <br /> | |||
</div> | </div> | ||
Version vom 2. Dezember 2020, 15:18 Uhr
1) Terme zusammenfassen
Einführung
Aufgaben
2) Terme ausmultiplizieren und faktorisieren
Terme ausmultiplizieren
Aufgabe
Terme faktorisieren
Aufgabe
Weitere Aufgaben zum Ausmultiplizieren und Faktorisieren
3) Binomische Formeln
Was sind die binomischen Formeln?
Herleitung der binomischen Formeln
Beispiele
Aufgaben
a)15()a()
b)3a()4b()3a()4b())
c)9u()2()
d)2m()7()
e)8y()10z()
f)6u()11w()6u()11w())
Klammere aus. Falls du dir unsicher bist, mache die Probe. Du kannst auch hier noch einmal vorbeischauen.
Schaue dir auch noch einmal die binomischen Formeln an und entscheide, wann du welche Formel anwenden kannst.