Digitale Werkzeuge in der Schule/Fit für VERA-8/Terme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 51: | Zeile 51: | ||
{{Box | 1=Aufgabe 2: Rechenaufgaben | 2= Fasse die folgenden Terme zusammen. Nutze dazu deinen Zettel und Stift, um die Rechenwege und Lösungen aufzuschreiben. <br/> | {{Box | 1=Aufgabe 2: Rechenaufgaben | 2= Fasse die folgenden Terme zusammen. Nutze dazu deinen Zettel und Stift, um die Rechenwege und Lösungen aufzuschreiben. <br/> | ||
a) <math> 15 \cdot 2+3 \cdot 5 \cdot 2+4 </math> | '''a)''' <math> 15 \cdot 2+3 \cdot 5 \cdot 2+4 </math> | ||
{{Lösung versteckt| 1= <math> 64 </math> | 2= Lösung | 3=Lösung einklappen}} | {{Lösung versteckt| 1= <math> 64 </math> | 2= Lösung | 3=Lösung einklappen}} | ||
| Zeile 60: | Zeile 60: | ||
b) <math> 3x-4y-2z+4y-2x</math> <br/> | '''b)''' <math> 3x-4y-2z+4y-2x</math> <br/> | ||
{{Lösung versteckt| 1= <math> x+8y-2z </math> | 2= Lösung | 3=Lösung einklappen}} | {{Lösung versteckt| 1= <math> x+8y-2z </math> | 2= Lösung | 3=Lösung einklappen}} | ||
| Zeile 69: | Zeile 69: | ||
c) <math> x \cdot 2 \cdot y+3x-y \cdot x </math> | '''c)''' <math> x \cdot 2 \cdot y+3x-y \cdot x </math> | ||
{{Lösung versteckt| 1= <math> xy+3x </math> | 2= Lösung | 3=Lösung einklappen}} | {{Lösung versteckt| 1= <math> xy+3x </math> | 2= Lösung | 3=Lösung einklappen}} | ||
| Zeile 78: | Zeile 78: | ||
d) <math> x \cdot y+x\cdot x+2 \cdot y+3 \cdot x \cdot 5 \cdot y </math> <br/> | '''d)''' <math> x \cdot y+x\cdot x+2 \cdot y+3 \cdot x \cdot 5 \cdot y </math> <br/> | ||
{{Lösung versteckt| 1= <math> 16xy+x^2+2y </math> | 2= Lösung | 3=Lösung einklappen}} | {{Lösung versteckt| 1= <math> 16xy+x^2+2y </math> | 2= Lösung | 3=Lösung einklappen}} | ||
| Zeile 87: | Zeile 87: | ||
e) <math> 2x+3xy-y+4x-2yx+y </math> | '''e)''' <math> 2x+3xy-y+4x-2yx+y </math> | ||
{{Lösung versteckt| 1= <math> 6x+xy </math> | 2= Lösung | 3=Lösung einklappen}} | {{Lösung versteckt| 1= <math> 6x+xy </math> | 2= Lösung | 3=Lösung einklappen}} | ||
| Zeile 96: | Zeile 96: | ||
f) <math> 12x-(12x+3y)+4y-(3x+2y) </math> <br/> | '''f)''' <math> 12x-(12x+3y)+4y-(3x+2y) </math> <br/> | ||
{{Lösung versteckt| 1= <math> -3x-y </math> | 2= Lösung | 3=Lösung einklappen}} | {{Lösung versteckt| 1= <math> -3x-y </math> | 2= Lösung | 3=Lösung einklappen}} | ||
| Zeile 106: | Zeile 106: | ||
g) <math> 4x-({1\over 4}y-(5x+3z)-(x+{5\over 8}y-2z)) </math> | '''g)''' <math> 4x-({1\over 4}y-(5x+3z)-(x+{5\over 8}y-2z)) </math> | ||
{{Lösung versteckt|1=Löse zuerst die Klammern auf, ordne dann die Summanden nach ihren Variablen. Mache danach noch die Brüche gleichnamig um danach alles zusammenfassen zu können.|2=Tipp|3=Tipp ausblenden}} | {{Lösung versteckt|1=Löse zuerst die Klammern auf, ordne dann die Summanden nach ihren Variablen. Mache danach noch die Brüche gleichnamig um danach alles zusammenfassen zu können.|2=Tipp|3=Tipp ausblenden}} | ||
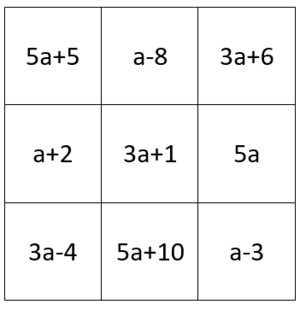
| Zeile 148: | Zeile 148: | ||
{{Lösung versteckt|1= Berechne zuerst die Summe der ersten Spalte. Diese Summe muss auch die Summe aller weiteren Zeilen, Spalten und Diagonalen sein | 2=Tipp | {{Lösung versteckt|1= Berechne zuerst die Summe der ersten Spalte. Diese Summe muss auch die Summe aller weiteren Zeilen, Spalten und Diagonalen sein | 2=Tipp 1 | 3=Tipp ausblenden}} | ||
{{Lösung versteckt|1=Wenn du die Summe der ersten Spalte berechnet hast, kannst du als nächstes die Summe der zweiten Zeile berechnen und in das noch auszufüllende Kästchen der zweiten Zeile den Term eintragen, der in der Summe noch fehlt, damit die Summe der ersten Spalt gleich der Summe der zweiten Zeile ist. | 2=Tipp 2 |3= Tipp ausblenden }} | {{Lösung versteckt|1=Wenn du die Summe der ersten Spalte berechnet hast, kannst du als nächstes die Summe der zweiten Zeile berechnen und in das noch auszufüllende Kästchen der zweiten Zeile den Term eintragen, der in der Summe noch fehlt, damit die Summe der ersten Spalt gleich der Summe der zweiten Zeile ist. | 2=Tipp 2 |3= Tipp ausblenden }} | ||
Version vom 28. November 2020, 14:59 Uhr
1) Terme zusammenfassen
Einführung
Aufgaben
2) Terme ausmultiplizieren und faktorisieren
Terme ausmultiplizieren
Aufgabe
Terme faktorisieren
Aufgabe
Weitere Aufgabenzum Ausmultiplizieren und Faktorisieren
3) Binomische Formeln
Einführung
Was sind die binomischen Formeln?
Herleitung der binomischen Formeln
Beispiele
Aufgabenteil
| 1. binomische Formel | |||
| 2. binomische Formel | |||
| 3. binomische Formel | |||
| Das ist keine binomische Formel |
a)15()a()
b)3a()4b()3a()4b())
c)9u()2()
d)2m()7()
e)8y()10z()
f)6u()17w()6u()17w())