Digitale Werkzeuge in der Schule/Fit für VERA-8/Stochastik: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 432: | Zeile 432: | ||
{{Box | Zufallsexperimente | | {{Box | Zufallsexperimente | | ||
Ein '''Zufallsexperiment''' ist ein Versuch mit zufälligem Ausgang. Zunächst schaust du, wie viele mögliche Ergebnisse es zu dem gefragten Ereignis gibt. Außerdem musst du die Zahl aller möglichen Ergebnisse betrachten. | |||
Die Wahrscheinlichkeit berechnet sich dann aus <math>\tfrac{\text{Anzahl der Ergebnisse zu gefragten Ereignis}}{\text{Anzahl aller möglichen Ergebnisse}} </math>. | Merksatz}} | |||
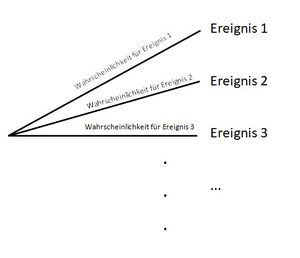
{{Box | Baumdiagramme| | {{Box | Baumdiagramme| | ||
| Zeile 456: | Zeile 458: | ||
2. Ein Mädchen wird gelost. | 2. Ein Mädchen wird gelost. | ||
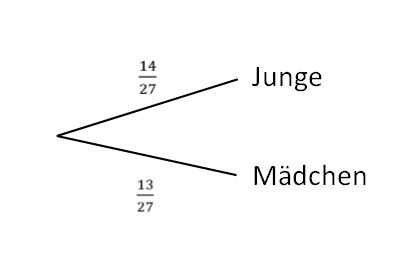
Die Wahrscheinlichkeiten ergeben sich aus den | Die Wahrscheinlichkeiten ergeben sich aus den relativen Häufigkeiten, also der tatsächlichen Anzahl an Jungen und Mädchen geteilt durch die Anzahl der Schülerinnen und Schüler in der Klasse. Das Baumdiagramm sieht dann so aus: | ||
[[Datei:Baumdiagramm A1 a.jpg|zentriert]] | [[Datei:Baumdiagramm A1 a.jpg|zentriert]] | ||
| Zeile 475: | Zeile 477: | ||
3. Die Lehrperson wird gelost. | 3. Die Lehrperson wird gelost. | ||
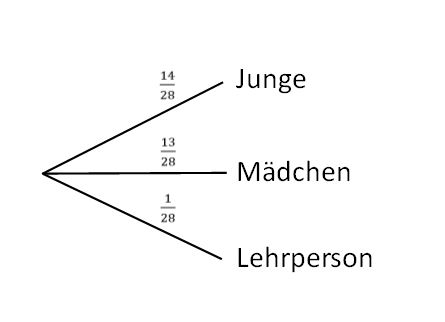
Auch hier ergeben sich die Wahrscheinlichen aus den | Auch hier ergeben sich die Wahrscheinlichen aus den relativen Häufigkeiten. Hierbei muss allerdings darauf geachtet werden, dass nicht nur die Anzahl der Schülerinnen und Schüler als gesamte Menge betrachtet wird, sondern auch die Lehrperson hinzu addiert wird. Es stehen also insgesamt 28 Personen zur Auswahl. Das Baumdiagramm sieht so aus: | ||
[[Datei:Baumdiagramm A1 b.jpg|zentriert]] | [[Datei:Baumdiagramm A1 b.jpg|zentriert]] | ||
| Zeile 526: | Zeile 528: | ||
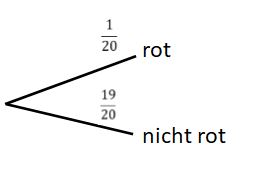
2. Die Kugel ist nicht gelb. | 2. Die Kugel ist nicht gelb. | ||
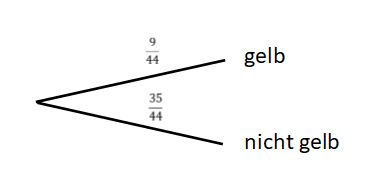
Die Wahrscheinlichkeit dafür, dass die Kugel gelb ist, ergibt sich dann aus der | Die Wahrscheinlichkeit dafür, dass die Kugel gelb ist, ergibt sich dann aus der relativen Häufigkeit der gelben Kugeln. Die Wahrscheinlichkeit dafür, dass die Kugel nicht gelb ist erfolgt aus der Komplementärregel. | ||
Das Baumdiagramm sieht dann so aus: | Das Baumdiagramm sieht dann so aus: | ||
| Zeile 540: | Zeile 542: | ||
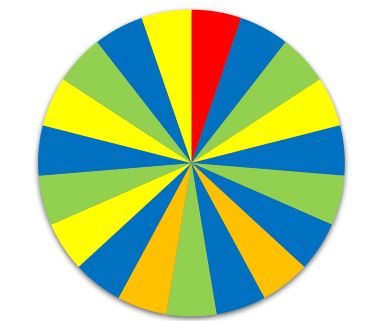
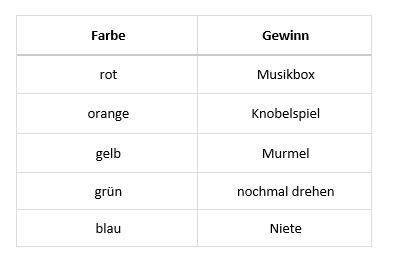
'''b)''' Oben auf dem Plakat steht: "Hier ist Gewinnen wahrscheinlicher, als Verlieren!". Stimmt das? Berechne zunächst die einzelnen Wahrscheinlichkeiten. Gibt die Lösung wieder in Prozent an. | '''b)''' Oben auf dem Plakat steht: "Hier ist Gewinnen wahrscheinlicher, als Verlieren!". Stimmt das? Berechne zunächst die einzelnen Wahrscheinlichkeiten. Gibt die Lösung wieder in Prozent an. | ||
{{Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele | {{Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?|2=Tipp|3=Tipp}} | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 560: | Zeile 562: | ||
4. Die Kugel ist blau. | 4. Die Kugel ist blau. | ||
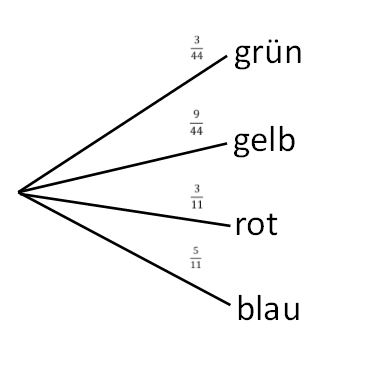
Die Wahrscheinlichkeit errechnet sich dann aus der | Die Wahrscheinlichkeit errechnet sich dann aus der relativen Häufigkeit der Kugeln. Das Baumdiagramm sieht dann so aus: | ||
[[Datei:Baumdiagramm A2 a.jpg|zentriert]] | [[Datei:Baumdiagramm A2 a.jpg|zentriert]] | ||
| Zeile 566: | Zeile 568: | ||
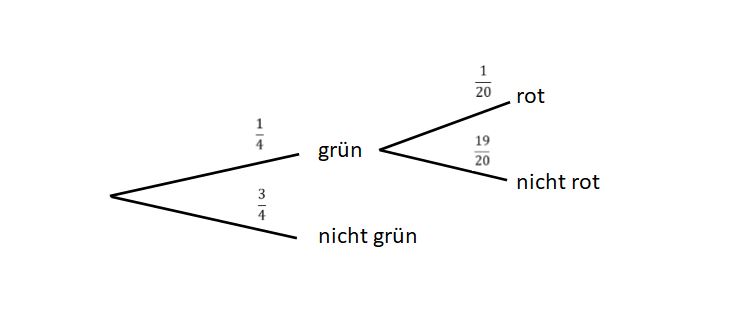
Optional kann eines mit 2 Ereignissen gezeichnet werden: | Optional kann eines mit 2 Ereignissen gezeichnet werden: | ||
Die Wahrscheinlichkeit für das Gewinnen ergibt sich aus der Komplementärregel. Die | Die Wahrscheinlichkeit für das Gewinnen ergibt sich aus der Komplementärregel. Die relative Häufigkeit der blauen Kugeln, mit denen man verliert, liegt bei <math>\tfrac{20}{44}=\tfrac{5}{11}</math>. Die Komplementärregel ergibt dann für das Gewinnen: <math>1-\tfrac{5}{11}=\tfrac{6}{11}</math>. | ||
Das Baumdiagramm sieht dann so aus: | Das Baumdiagramm sieht dann so aus: | ||
Version vom 21. November 2020, 10:33 Uhr
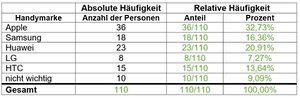
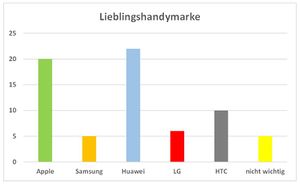
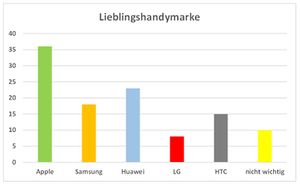
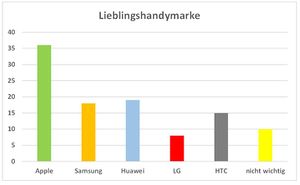
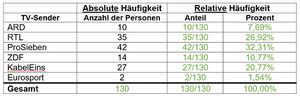
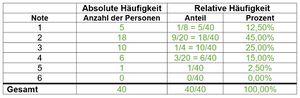
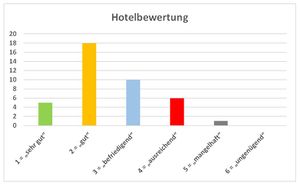
Absolute und relative Häufigkeit
Zufallsexperimente
Laplace-Experimente