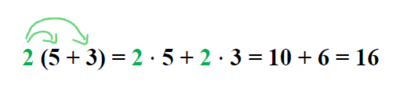Digitale Werkzeuge in der Schule/Fit für VERA-8/Terme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 7: | Zeile 7: | ||
====Einführung==== | ====Einführung==== | ||
=====Wie kann ich Terme zusammenfassen?===== | =====Wie kann ich Terme zusammenfassen?===== | ||
{{Box |1= Rechenregeln | 2=Terme erhalten unterschiedliche Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division. Manche Teile von Termen kann man zusammenfassen, um so den Term zu vereinfachen. Beachte dabei: <br/> | {{Box |1= Rechenregeln | 2=Terme erhalten unterschiedliche Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division. Manche Teile von Termen kann man zusammenfassen, um so den Term zu vereinfachen. Beachte dabei: <br/> <br/> | ||
'''Beim Zusammenfassen von Summen gilt:''' <br/> Nur gleiche Variablen in der gleichen Potenz dürfen zusammengefasst werden. <br/> | '''Beim Zusammenfassen von Summen gilt:''' <br/> Nur gleiche Variablen in der gleichen Potenz dürfen zusammengefasst werden. <br/> | ||
Beispiele: <br/> | Beispiele: <br/> | ||
<math> 2a^2+a+3a </math> <br/> | 1) <math> 2a^2+a+3a </math> <br/> | ||
<math> = 2a^2+4a</math> <br/> <br/> | <math> = 2a^2+4a</math> <br/> <br/> | ||
<math> 2x+xy-3y^2-2xy+2xy^2 </math> <br/> | 2) <math> 2x+xy-3y^2-2xy+2xy^2 </math> <br/> | ||
<math>= 2x-3y^2+2xy^2+ | <math>= 2x-3y^2+2xy^2+xy-2xy </math> <br/> | ||
<math>= 2x-3y^2+2xy^2-xy </math> <br/> | <math>= 2x-3y^2+2xy^2-xy </math> <br/> | ||
Hier konnten nur die beiden Teile mit xy zusammengefasst werden, da alle anderen Variablen unterschiedlich sind bzw. in einer anderen Potenz vorkommen. <br/> <br/> | Hier konnten nur die beiden Teile mit xy zusammengefasst werden, da alle anderen Variablen unterschiedlich sind bzw. in einer anderen Potenz vorkommen. <br/> <br/> | ||
<math> {\color{blue}2x}{\color{red}+4y}{\color{green}-xy}{\color{red}+2y}{\color{blue}-3x}{\color{green}+5xy}</math> <br/> | 3) <math> {\color{blue}2x}{\color{red}+4y}{\color{green}-xy}{\color{red}+2y}{\color{blue}-3x}{\color{green}+5xy}</math> <br/> | ||
<math> = {\color{blue}-x}{\color{red}+6y}{\color{green}+4xy} </math> <br/> | <math> = {\color{blue}-x}{\color{red}+6y}{\color{green}+4xy} </math> <br/> | ||
Tipp: Es kann helfen die gleichen Potenzen und Variablen farblich zu markieren. | Tipp: Es kann helfen die gleichen Potenzen und Variablen farblich zu markieren. <br/> <br/> | ||
| Zeile 44: | Zeile 44: | ||
===Aufgabenteil=== | ===Aufgabenteil=== | ||
{{Box | Aufgabe 1: | | {{Box | Aufgabe 1: Wer wird Millionär? | | ||
{{LearningApp|width=100%|height=500px|app=1704712}} | Arbeitsmethode| Farbe={{Farbe|orange}}}} | {{LearningApp|width=100%|height=500px|app=1704712}} | Arbeitsmethode| Farbe={{Farbe|orange}}}} | ||
{{Box | 1=Aufgabe 2: | 2= Fasse die folgenden Terme zusammen | {{Box | 1=Aufgabe 2: Rechnungen | 2= Fasse die folgenden Terme zusammen. Nutze dazu deinen Zettel und Stift, um die Rechenwege und Lösungen aufzuschreiben. <br/> | ||
a) <math> 15 \cdot 2+3 \cdot 5 \cdot 2+4 </math> | a) <math> 15 \cdot 2+3 \cdot 5 \cdot 2+4 </math> | ||
| Zeile 120: | Zeile 120: | ||
| 3=Arbeitsmethode }} | | 3=Arbeitsmethode }} | ||
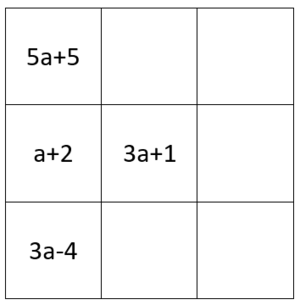
{{Box| 1=Aufgabe 3: magisches Quadrat | 2= Die Summe jeder Zeile, Spalte und Diagonale | {{Box| 1=Aufgabe 3: magisches Quadrat | 2= Die Summe jeder Zeile, Spalte und Diagonale des magischen Quadrats ergeben gleichwertige Terme, das heißt wenn du eine Zeile addierst, kommt das gleiche raus wie bei allen anderen Zeilen, Spalten und Diagonalen. Ergänze die fehlenden Terme. Nutze dazu deinen Zettel und Stift. <br/> | ||
[[Datei:Magisches Dreieck.png|mini|center]] | [[Datei:Magisches Dreieck.png|mini|center]] | ||
| Zeile 129: | Zeile 129: | ||
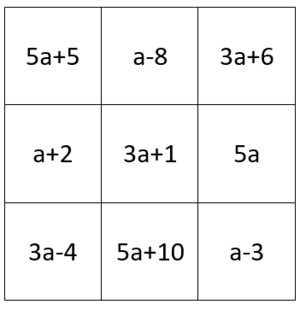
{{Lösung versteckt|1= [[Datei:Magisches Dreieck ausgefüllt.png|mini|center]] | {{Lösung versteckt|1= [[Datei:Magisches Dreieck ausgefüllt.png|mini|center]] | ||
|2=Lösung|3=Lösung ausblenden}}|Farbe={{Farbe|grün}} }} | |2=Lösung|3=Lösung ausblenden}}|Farbe={{Farbe|grün}} |3=Arbeitsmethode}} | ||
===2) Terme ausmultiplizieren und faktorisieren=== | ===2) Terme ausmultiplizieren und faktorisieren=== | ||
Version vom 21. November 2020, 15:07 Uhr
1) Terme zusammenfassen
Einführung
Wie kann ich Terme zusammenfassen?
Aufgabenteil
2) Terme ausmultiplizieren und faktorisieren
Terme ausmultiplizieren
Aufgabe
Terme faktorisieren
Aufgabe
Weitere Aufgabenzum Ausmultiplizieren und Faktorisieren
3) Binomische Formeln
Einführung
Was sind die binomischen Formeln?
Herleitung der binomischen Formeln
Beispiele
Aufgabenteil
| 1. binomische Formel | |||
| 2. binomische Formel | |||
| 3. binomische Formel | |||
| Das ist keine binomische Formel |
a)15()a()
b)3a()4b()3a()4b())
c)9u()2()
d)2m()7()
e)8y()10z()
f)6u()17w()6u()17w())