Buss-Haskert/Zweistufige Zufallsexperimente/Zweistufige Zufallsexperimente: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
K (Formatierungen)
Markierung: 2017-Quelltext-Bearbeitung
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 129: Zeile 129:
das Ereignis "einmal Rot, einmal Blau" setzt sich zusammen aus den Ergebnissen (r,b) und (b,r), wende zuerst die Produktregel und dann die Summenregel an.|Tipp zu Nr. 1b|Verbergen}}</div>
das Ereignis "einmal Rot, einmal Blau" setzt sich zusammen aus den Ergebnissen (r,b) und (b,r), wende zuerst die Produktregel und dann die Summenregel an.|Tipp zu Nr. 1b|Verbergen}}</div>
</div>
</div>
{{Lösung versteckt|1=Zeichne ein Baumdiagramm. Die erste Stufe ist der Zug eines Buchstabens aus dem Gefäß mit Vokalen. Dies sind dementsprechend die möglichen Ausgänge a, i ,u und o (Pfade). Die Wahrscheinlichkeit, z.B. den Vokal "a" zu ziehen, beträgt <math>\tfrac{4}{8}</math> = <math>\tfrac{1}{2}</math>, da es 4 Karten mit dem Buchstaben "a" gibt von 8 Karten insgesamt.<br> Die zweite Stufe ist der Zug eines Buchstabens aus dem Gefäß mit den Konsonanten, also sind dies auch jeweils die möglichen Ausgänge (Pfade). Die Wahrscheinlichkeit, z.B. den Konsonaten "h" zu ziehen, beträgt <math>\tfrac{2}{8}</math> = <math>\tfrac{1}{4}</math>, da es 2 Karten mit dem Buchstaben "h" gibt von 8 Karten insgesamt.|2=Tipp zu Nr. 2 (Baumdiagramm)|3=Verbergen}}
<div class="grid">
{{Lösung versteckt|Die gesuchten Wahrscheinlichkeiten sind immer Wahrscheinlichkeiten von einzelnen Ergebnissen, wende also jeweils die Produktregel an.<br>zu g) (a,u) ist ein unmögliches Ereignis, da zwei Vokale gezogen werden sollen, aber im zweiten Gefäß nur Konsonanten enthalten sind. Daher gilt P(a,u) = 0.<br>zu h) (i,f) ist ebensfalls ein unmögliches Ereignis, da im zweiten Gefäß der Buchstabe "f" nicht enthalten ist.|Tipp zu Nr. 2 (Wahrscheinlichkeiten)|Verbergen}}
<div class="width-1-2">{{Lösung versteckt|1=Zeichne ein Baumdiagramm. Die erste Stufe ist der Zug eines Buchstabens aus dem Gefäß mit Vokalen. Dies sind dementsprechend die möglichen Ausgänge a, i ,u und o (Pfade). Die Wahrscheinlichkeit, z.B. den Vokal "a" zu ziehen, beträgt <math>\tfrac{4}{8}</math> = <math>\tfrac{1}{2}</math>, da es 4 Karten mit dem Buchstaben "a" gibt von 8 Karten insgesamt.<br> Die zweite Stufe ist der Zug eines Buchstabens aus dem Gefäß mit den Konsonanten, also sind dies auch jeweils die möglichen Ausgänge (Pfade). Die Wahrscheinlichkeit, z.B. den Konsonaten "h" zu ziehen, beträgt <math>\tfrac{2}{8}</math> = <math>\tfrac{1}{4}</math>, da es 2 Karten mit dem Buchstaben "h" gibt von 8 Karten insgesamt.|2=Tipp zu Nr. 2 (Baumdiagramm)|3=Verbergen}}</div>
{{Lösung versteckt|Es handelt sich um ein zweistufiges Zufallsexperiment. Das Baumdiagramm hat als Stufen den ersten und zweiten Zug einer Kugel. Die einzelnen Pfade (Äste) sind die Farben blau, gelb, rot und grün. Die Wahrscheinlichkeiten der Pfade ergeben sich aus der Farbverteilung. Da die Kugeln wieder zurückgelegt werden, bleiben beim zweiten Zug die Wahrscheinlichkeiten für die einzelnen Pfade gleich.|Tipp zu Nr. 3 (Baumdiagramm)|Verbergen}}
<div class="width-1-2">{{Lösung versteckt|1=Die gesuchten Wahrscheinlichkeiten sind immer Wahrscheinlichkeiten von einzelnen Ergebnissen, wende also jeweils die Produktregel an.<br>zu g) (a,u) ist ein unmögliches Ereignis, da zwei Vokale gezogen werden sollen, aber im zweiten Gefäß nur Konsonanten enthalten sind. Daher gilt P(a,u) = 0.<br>zu h) (i,f) ist ebensfalls ein unmögliches Ereignis, da im zweiten Gefäß der Buchstabe "f" nicht enthalten ist.|2=Tipp zu Nr. 2 (Wahrscheinlichkeiten)|3=Verbergen}}</div>
{{Lösung versteckt|Die Aufgabenteile a, b und c beziehen sich auf die Ergebnisse a) (r,b), b) (b,r) und c) (r,r). Berechne die Wahrscheinlichkeiten also mit der Produktregel.<br>
</div>
<div class="grid">
<div class="width-1-2">{{Lösung versteckt|1=Es handelt sich um ein zweistufiges Zufallsexperiment. Das Baumdiagramm hat als Stufen den ersten und zweiten Zug einer Kugel. Die einzelnen Pfade (Äste) sind die Farben blau, gelb, rot und grün. Die Wahrscheinlichkeiten der Pfade ergeben sich aus der Farbverteilung. Da die Kugeln wieder zurückgelegt werden, bleiben beim zweiten Zug die Wahrscheinlichkeiten für die einzelnen Pfade gleich.|2=Tipp zu Nr. 3 (Baumdiagramm)|3=Verbergen}}</div>
<div class="width-1-2">{{Lösung versteckt|1=Die Aufgabenteile a, b und c beziehen sich auf die Ergebnisse a) (r,b), b) (b,r) und c) (r,r). Berechne die Wahrscheinlichkeiten also mit der Produktregel.<br>
In Aufgabenteil d) lautet das Ereignis E:"Die erste Kugel ist rot." Hier sind also die Ergebnisse (r,b), (r,ge), (r,r) und (r,gr) günstige Ergebnisse. Wende also zunächst die Produkt- und dann die Summenregel an.<br>Für Schnelldenker: Die Summe der Pfadwahrscheinlichkeiten einer Verzweigung beträgt immer 1 (denn es wird ja sicher eine Kugel der Farbe blau, gelb, rot oder grün gezogen). Daher ist die Wahrscheinlichkeit für das Ereignis E:"Die erste Kugel ist rot" gleich P(r).<br>
In Aufgabenteil d) lautet das Ereignis E:"Die erste Kugel ist rot." Hier sind also die Ergebnisse (r,b), (r,ge), (r,r) und (r,gr) günstige Ergebnisse. Wende also zunächst die Produkt- und dann die Summenregel an.<br>Für Schnelldenker: Die Summe der Pfadwahrscheinlichkeiten einer Verzweigung beträgt immer 1 (denn es wird ja sicher eine Kugel der Farbe blau, gelb, rot oder grün gezogen). Daher ist die Wahrscheinlichkeit für das Ereignis E:"Die erste Kugel ist rot" gleich P(r).<br>
In Aufgabenteil e) lautet das Ereignis E:"Die zweite Kugel ist rot." Hier sind also die Ergebnisse (b,r), (ge,r), (r,r) und (gr,r) günstige Ergebnisse. Vergleiche mit Aufgabenteil d).<br>
In Aufgabenteil e) lautet das Ereignis E:"Die zweite Kugel ist rot." Hier sind also die Ergebnisse (b,r), (ge,r), (r,r) und (gr,r) günstige Ergebnisse. Vergleiche mit Aufgabenteil d).<br>
In Aufgabenteil f) lautet das Ereignis E:"Keine Kugel ist rot." Hier sind also die Ergebnisse (b,b), (b,ge), (b,gr), (ge,b), (ge,ge), (ge,gr), (gr,b), (gr,ge), (gr,gr) günstige Ergebnisse. Wende also zunächst die Produkt- und dann die Summenregel an.|Tipp zu Nr. 3 (Wahrscheinlichkeiten)|Verbergen}}
In Aufgabenteil f) lautet das Ereignis E:"Keine Kugel ist rot." Hier sind also die Ergebnisse (b,b), (b,ge), (b,gr), (ge,b), (ge,ge), (ge,gr), (gr,b), (gr,ge), (gr,gr) günstige Ergebnisse. Wende also zunächst die Produkt- und dann die Summenregel an.|2=Tipp zu Nr. 3 (Wahrscheinlichkeiten)|3=Verbergen}}</div>
</div>
{{Lösung versteckt|1=Die Aufgabenteile a, b und c beziehen sich auf die Ergebnisse a) (r,b), b) (b,r) und c) (r,r). Berechne die Wahrscheinlichkeiten also mit der Produktregel.<br>
In Aufgabenteil d) lautet das Ereignis E:"Die erste Kugel ist rot." Hier sind also die Ergebnisse (r,b), (r,ge), (r,r) und (r,gr) günstige Ergebnisse. Wende also zunächst die Produkt- und dann die Summenregel an.<br>Für Schnelldenker: Die Summe der Pfadwahrscheinlichkeiten einer Verzweigung beträgt immer 1 (denn es wird ja sicher eine Kugel der Farbe blau, gelb, rot oder grün gezogen). Daher ist die Wahrscheinlichkeit für das Ereignis E:"Die erste Kugel ist rot" gleich P(r).<br>
In Aufgabenteil e) lautet das Ereignis E:"Die zweite Kugel ist rot." Hier sind also die Ergebnisse (b,r), (ge,r), (r,r) und (gr,r) günstige Ergebnisse. Vergleiche mit Aufgabenteil d).<br>
In Aufgabenteil f) lautet das Ereignis E:"Keine Kugel ist rot." Hier sind also die Ergebnisse (b,b), (b,ge), (b,gr), (ge,b), (ge,ge), (ge,gr), (gr,b), (gr,ge), (gr,gr) günstige Ergebnisse. Wende also zunächst die Produkt- und dann die Summenregel an.|2=Tipp zu Nr. 3 (Wahrscheinlichkeiten)|3=Verbergen}}
{{Lösung versteckt|Berechne die Wahrscheinlichkeiten der Ergebnisse mit der Produktregel.|Tipp zu Nr. 4|Verbergen}}
{{Lösung versteckt|Berechne die Wahrscheinlichkeiten der Ergebnisse mit der Produktregel.|Tipp zu Nr. 4|Verbergen}}


Version vom 12. November 2020, 14:41 Uhr

3) Zweistufige Zufallsexperimente

Experiment
Nimm eine Münze, wirf sie zweimal und notiere jeweils das Ergebnis. Wie kannst du diese Ergebnisse übersichtlich darstellen?
Wie groß ist die Wahrscheinlichkeit für das Ergebnis (Z,Z)?
Video laden
YouTube

Die Darstellung, die im Video verwendet wird, heißt Baumdiagramm.

3.1 Wie zeichne ich ein Baumdiagramm?

Ein Baumdiagramm zeichnen Schritt für Schritt
Urne 3 rot, 5 blau, 2 gelb.png
In einer Urne befinden sich 3 rote, 5 blaue und 2 gelbe Kugeln. Es werden nacheinander zwei Kugeln gezogen,die Farbe wird notiert und die Kugel wird nach dem Zug zurückgelegt. Erstelle ein Baumdiagramm und beschrifte es vollständig.

Ein Baumdiagramm besteht aus einer verschiedenen Anzahl von Pfaden (Ästen) und Stufen. Zweistufige Zufallsexperimente bestehen immer aus zwei Stufen, mehrstufige Zufallsexperimente aus mehreren Stufen. Bevor du ein Baumdiagramm zeichnest, überlege genau, welche Bedeutung die Stufen im Experiment haben und welche Bedeutung die Pfade (Äste).
Du kannst es von links nach rechts zeichnen oder von oben nach unten. Du beginnst jedes Baumdiagramm mit dem Zeichnen von Pfaden (Ästen).


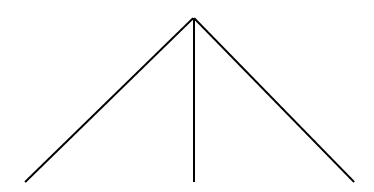
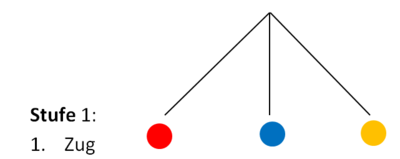
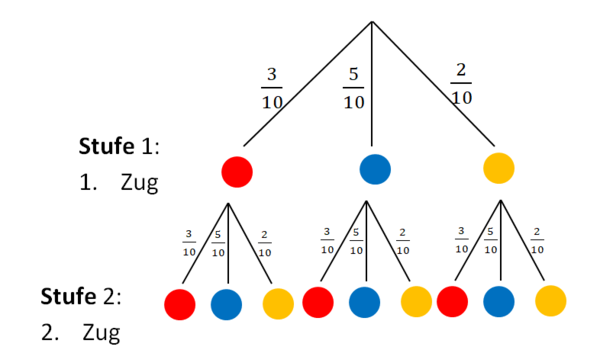
1. Zeichne die Pfade (Äste). (Achte darauf, dass die Aste auf einer Linie enden.) Wie viele Äste du zeichnen musst, hängt davon ab, wie viele mögliche Ausgänge es in dieser Stufe gibt. Hier hast du 3 mögliche Ergebnisse: eine rote, blaue oder gelbe Kugel ziehen.


Von links nach rechts gezeichnet:
Von oben nach unten gezeichnet:
Baumdiagramm zeichnen 1.png
Baumdiagramm zeichnen 1 2.png

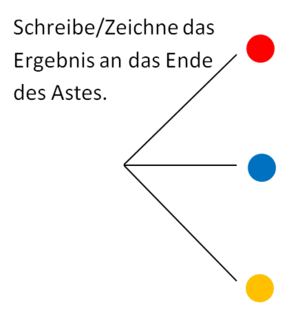
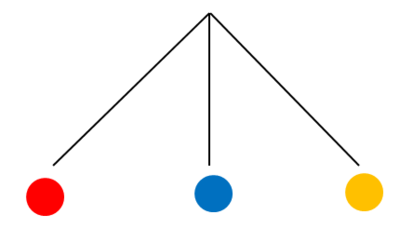
2. Ergänze die möglichen Ausgänge.

Baumdiagramm zeichnen 2.png
Baumdiagramm zeichnen 2 2.png

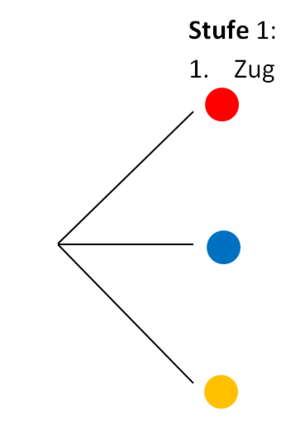
Hier entspricht also die 1. Stufe des Baumdiagramms dem 1. Ziehen einer Kugel.

Baumdiagramm zeichnen 3.png
Baumdiagramm zeichnen 3 1.png

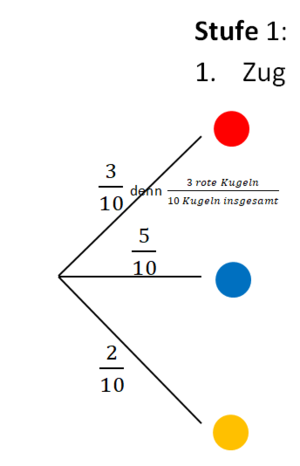
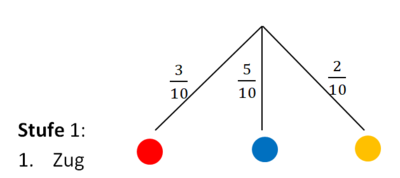
3. Schreibe die jeweiligen Wahrscheinlichkeiten an die Pfade (Äste).

Baumdiagramm zeichnen 4.png
Baumdiagramm zeichnen 4 3.png

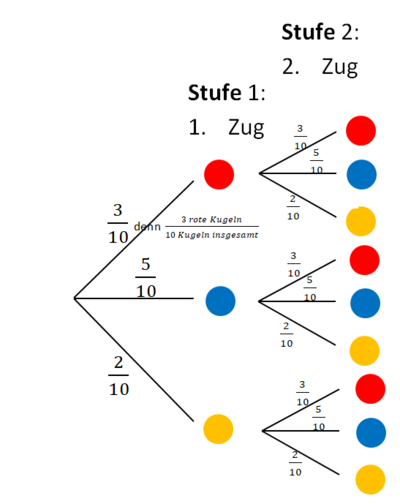
4. Nun wiederholst du das Vorgehen für die 2. Stufe, den 2. Ziehen einer Kugel. Zeichne an jeden Ausgang der 1. Stufe erneut Pfade (Äste) mit den möglichen Ausgängen und den zugehörigen Wahrscheinlichkeiten.

Baumdiagramm zeichnen 4 1.png
Baumdiagramm zeichnen 4 4.png


Ergebnisse zweistufiger Zufallsexperimente
Die Ergebnisse eines zweistufigen Zufallsexperimentes sind geordnete Paare.
Baumdiagramm zeichnen 5 1.png
Baumdiagramm zeichnen 5 2.png

3.2 Wie berechne ich Wahrscheinlichkeiten (mithilfe eines Baumdiagramms)?

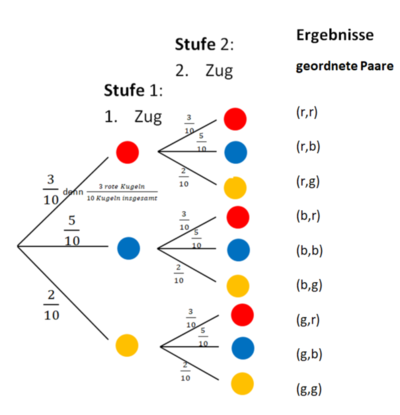
Um zu einem möglichen Ergebnis zu gelangen, musst du einen bestimmten Pfad des Baumdiagrammes gehen. Die Wahrscheinlichkeit dieses Ergebnisses berechnest du, indem du die Wahrscheinlichkeiten entlang des Pfades multiplizierst. Beispiel:
P(r,b) = ∙ = = 0,15 = 15%
P(b,r) = ∙ = = 0,15 = 15%


Produktregel
Bei einem zweistufigen Zufallsversuch wird die Wahrscheinlichkeit eines Ergebnisses (geordnetes Paar) berechnet, indem die Wahrscheinlichkeiten entlang des zugehörigen Pfades multipliziert werden.
Video laden
YouTube


Übung 1

Bestimme für das Zufallsexperiment oben:
a) P(erst gelb, dann rot)

b) P(zweimal rot)
P(erst gelb, dann rot) lässt sich kürzer schreiben als P(g,r). Gehe den Pad des Baumdiagramms entlang bis zu diesem Ergebnis und multipliziere die Wahrscheinlichkeiten entlang des Pfades.
P(zweimal rot) lässt sich kürzer schreiben als P(r,r). Gehe den Pfad des Baumdiagramms entlang bis zu diesem Ergebnis und multipliziere die Wahrscheinlichkeiten entlang des Pfades.


Nun betrachten wir nicht mehr nur einzelne Ergebnisse sondern berechnen die Wahrscheinlichkeiten von Ereignissen.
Ein Ereignis setzt sich aus mehreren günstigen Ergebnissen zusammen.
Beispiel:
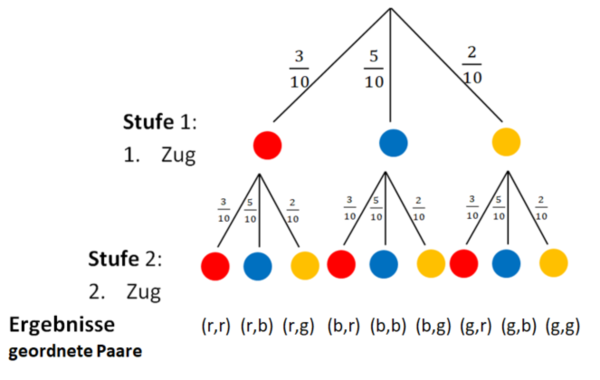
Das Ereignis E: "Eine rote und eine blaue Kugel wird gezogen" setzt sich aus den Ergebnissen (r,b) und (b,r) zusammen.

Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, werden die einzelnen Wahrscheinlichkeiten der günstigen Ergebnisse (geordnete Paare) addiert.
Beispiel:
E: "Eine rote und eine blaue Kugel wird gezogen"
P(E) = P(r,b) + P(b,r)
       = +
       = = 0,3 = 30%


Summenregel
Die Wahrscheinlichkeit eines Ereignisses wird berechnet, indem die Wahrscheinlichkeiten von allen günstigen Ergebnissen, die zu diesem Ereignis gehören, addiert werden.
Video laden
YouTube


Übung 2

Bestimme für das Zufallsexperiment oben:
a) P(E1) für E1:"eine rote und eine gelbe Kugel ziehen"

b) P(E2) für E2:"Die zweite Kugel ist rot"
Das Ereignis E1 setzt sich zusammen aus den Ergebnissen (r,g) und (g,r). Berechne die Wahrscheinlichkeiten dieser Ergebnisse, also P(r,g)= ... und P(g,r)= ... mit der Produktregel.
Nun berechne die Wahrscheinlichkeit des Ereignisses P(E1) = P(r,g) + P(g,r) mithilfe der Summenregel.
Das Ereignis E2 setzt sich zusammen aus den Ergebnissen (r,r), (b,r) und (g,r). Berechne die Wahrscheinlichkeiten dieser Ergebnisse, also P(r,r)= ..., P(b,r)=... und P(g,r)= ... mit der Produktregel.
Nun berechne die Wahrscheinlichkeit des Ereignisses P(E2) = P(r,r) + P(b,r) + P(g,r) mithilfe der Summenregel.


Wahrscheinlichkeiten berechnen mit der Produkt-und Summenregel (Pfadregeln)

Gehe zur Berechnung von Wahrscheinlichkeiten bei zweistufigen Zufallsexperimenten schrittweise vor:
1. Zeichne ein Baumdiagramm. Überlege dazu, welche Bedeutung die einzelnen Stufen und Pfade (Äste) haben. Beschrifte die Pfade (Äste) des Baumdiagramms mit den zugehörigen Wahrscheinlichkeiten.
2. Markiere die für das Ereignis E günstigen Ergebnisse (geordnete Paare). Berechne die jeweiligen Wahrscheinlichkeiten mit der Produktregel.

3. Berechne die Wahrscheinlichkeit P(E) des Ereignisses mit der Summenregel.

Übertrage das Beispiel in dein Heft:

Urne 3 rot, 7 blau.png

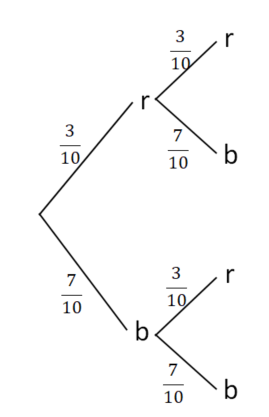
In einer Urne befinden sich 7 blaue und 3 rote Kugeln. Nacheinander wird zweimal eine Kugel gezogen, die Farbe notiert und die Kugel dann wieder zurückgelegt.
Bestimme die Wahrscheinlichkeit für das Ereignis, eine rote und eine blaue Kugel zu ziehen.

Gehe zur Lösung der Aufgabe schrittweise vor, wie oben beschrieben.

1. Schritt: Zeichne ein Baumdiagramm und beschrifte es.
Baumdiagramm 3rot 7blau.png

2. Schritt:
Das Ereignis E: "eine rote und eine blaue Kugel ziehen" setzt sich zusammen aus den einzelnen Ergebnissen (r,b) und (b,r).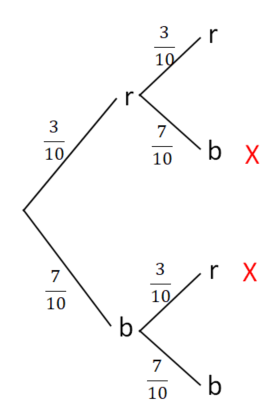
Baumdiagramm 3rot 7blau mit Markierungen.png
P(r,b) = ∙ = = 0,21 = 21%

P(b,r) = ∙ = = 0,21 = 21%

3. Schritt:
P(E) = P(r,b) + P(b,r)
          =+

          = = = 0,42 = 42%

Mit dem nachfolgenden GeoGebra-Applet (von Herrn Wengler) kannst du verschiedenste Urnenexperimente simulieren. Stelle das Experiment von oben nach.

Link zum Applet


Übung 3
Löse Buch S. 38 Nr. 1, 2, 3 und 4
Die zwei Stufen des Experimentes sind die zwei Drehungen des Glückrades. Die Pfade (Äste) sind die möglichen Ausgänge, die verschiedenen Farben.

"zweimal hintereinander Rot" ist das Ergebnis (r,r), wende die Produktregel an.
"erst Rot, dann Blau" ist das Ergebnis (r,b), wende die Produktregel an

das Ereignis "einmal Rot, einmal Blau" setzt sich zusammen aus den Ergebnissen (r,b) und (b,r), wende zuerst die Produktregel und dann die Summenregel an.
Zeichne ein Baumdiagramm. Die erste Stufe ist der Zug eines Buchstabens aus dem Gefäß mit Vokalen. Dies sind dementsprechend die möglichen Ausgänge a, i ,u und o (Pfade). Die Wahrscheinlichkeit, z.B. den Vokal "a" zu ziehen, beträgt = , da es 4 Karten mit dem Buchstaben "a" gibt von 8 Karten insgesamt.
Die zweite Stufe ist der Zug eines Buchstabens aus dem Gefäß mit den Konsonanten, also sind dies auch jeweils die möglichen Ausgänge (Pfade). Die Wahrscheinlichkeit, z.B. den Konsonaten "h" zu ziehen, beträgt = , da es 2 Karten mit dem Buchstaben "h" gibt von 8 Karten insgesamt.
Die gesuchten Wahrscheinlichkeiten sind immer Wahrscheinlichkeiten von einzelnen Ergebnissen, wende also jeweils die Produktregel an.
zu g) (a,u) ist ein unmögliches Ereignis, da zwei Vokale gezogen werden sollen, aber im zweiten Gefäß nur Konsonanten enthalten sind. Daher gilt P(a,u) = 0.
zu h) (i,f) ist ebensfalls ein unmögliches Ereignis, da im zweiten Gefäß der Buchstabe "f" nicht enthalten ist.
Es handelt sich um ein zweistufiges Zufallsexperiment. Das Baumdiagramm hat als Stufen den ersten und zweiten Zug einer Kugel. Die einzelnen Pfade (Äste) sind die Farben blau, gelb, rot und grün. Die Wahrscheinlichkeiten der Pfade ergeben sich aus der Farbverteilung. Da die Kugeln wieder zurückgelegt werden, bleiben beim zweiten Zug die Wahrscheinlichkeiten für die einzelnen Pfade gleich.

Die Aufgabenteile a, b und c beziehen sich auf die Ergebnisse a) (r,b), b) (b,r) und c) (r,r). Berechne die Wahrscheinlichkeiten also mit der Produktregel.
In Aufgabenteil d) lautet das Ereignis E:"Die erste Kugel ist rot." Hier sind also die Ergebnisse (r,b), (r,ge), (r,r) und (r,gr) günstige Ergebnisse. Wende also zunächst die Produkt- und dann die Summenregel an.
Für Schnelldenker: Die Summe der Pfadwahrscheinlichkeiten einer Verzweigung beträgt immer 1 (denn es wird ja sicher eine Kugel der Farbe blau, gelb, rot oder grün gezogen). Daher ist die Wahrscheinlichkeit für das Ereignis E:"Die erste Kugel ist rot" gleich P(r).
In Aufgabenteil e) lautet das Ereignis E:"Die zweite Kugel ist rot." Hier sind also die Ergebnisse (b,r), (ge,r), (r,r) und (gr,r) günstige Ergebnisse. Vergleiche mit Aufgabenteil d).

In Aufgabenteil f) lautet das Ereignis E:"Keine Kugel ist rot." Hier sind also die Ergebnisse (b,b), (b,ge), (b,gr), (ge,b), (ge,ge), (ge,gr), (gr,b), (gr,ge), (gr,gr) günstige Ergebnisse. Wende also zunächst die Produkt- und dann die Summenregel an.

Die Aufgabenteile a, b und c beziehen sich auf die Ergebnisse a) (r,b), b) (b,r) und c) (r,r). Berechne die Wahrscheinlichkeiten also mit der Produktregel.
In Aufgabenteil d) lautet das Ereignis E:"Die erste Kugel ist rot." Hier sind also die Ergebnisse (r,b), (r,ge), (r,r) und (r,gr) günstige Ergebnisse. Wende also zunächst die Produkt- und dann die Summenregel an.
Für Schnelldenker: Die Summe der Pfadwahrscheinlichkeiten einer Verzweigung beträgt immer 1 (denn es wird ja sicher eine Kugel der Farbe blau, gelb, rot oder grün gezogen). Daher ist die Wahrscheinlichkeit für das Ereignis E:"Die erste Kugel ist rot" gleich P(r).
In Aufgabenteil e) lautet das Ereignis E:"Die zweite Kugel ist rot." Hier sind also die Ergebnisse (b,r), (ge,r), (r,r) und (gr,r) günstige Ergebnisse. Vergleiche mit Aufgabenteil d).

In Aufgabenteil f) lautet das Ereignis E:"Keine Kugel ist rot." Hier sind also die Ergebnisse (b,b), (b,ge), (b,gr), (ge,b), (ge,ge), (ge,gr), (gr,b), (gr,ge), (gr,gr) günstige Ergebnisse. Wende also zunächst die Produkt- und dann die Summenregel an.
Berechne die Wahrscheinlichkeiten der Ergebnisse mit der Produktregel.


Übung 4
Löse Buch S. 39 Nr. 5, 6, 10 und 11.
Ein Tetraeder ist ein Körper mit vier Seitenflächen (die jeweils gleichseitige Dreiecke sind).
Die zwei Stufen des Baumdiagramms sind der erste und zweite Wurf des Würfels, die Pfade (Äste) sind jeweils die Zahlen 1, 2, 3 und 4.
Die zwei Stufen des Baumdiagramms sind der erste und zweite Wurf der Reißzwecke, die Pfade (Äste) sind jeweils die Lagen "Kopf" oder "Seite" mit den angegebenen Wahrscheinlichkeiten.
Berechne die Wahrscheinlichkeit des Ergebnisses P(S,S) mit der Produktregel.
Die zwei Stufen des Baumdiagramms sind der erste und zweite Schwangerschaftstest. Die Pfade (Äste) sind jeweils die möglichen Ausgänge "Die Schwangerschaft wird angezeigt (bei bestehender Schwangerschaft)" und "Die Schwangerschaft wird nicht angezeigt (bei bestehender Schwangerschaft)", mit den Wahrscheinlichkeiten von 0,99(=99%) und 0,01(=1%). Berechne die Wahrscheinlichkeit von (nicht angezeigt, nicht angezeigt) mit der Produktregel.
Um die Häufigkeit dieses Ergebnisses bei 100000 Test zu berechnen, multipliziere die Wahrscheinlichkeit mit 100000.
Die 1. Stufe des Baumdiagramms ist die Entscheidung für einen Behälter. Die Pfade (Äste) führen also zu den Ausängen Behälter (1), (2) und (3) mit jeweils der Wahrscheinlichkeit .
Die 2. Stufe des Baumdiagramms ist dann der Zug einer Kugel. Die Pfade (Äste) führen also zu den Ausgängen schwarz oder weiß. Die Wahrscheinlichkeiten für diese Äste sind unterschiedlich, je nach Farbverteilung im jeweiligen Behälter.
Zeichne ein neues Baumdiagramm entsprechend der neuen Verteilung der Kugeln. Es Ändern sich die Pfade und Wahrscheinlichkeiten der zweiten Stufe.
Überlegt zu zweit. Stellt das Experiment mit nach, die Materialien erhaltet ihr von eurer Lehrerin.


Sprinteraufgabe
Löse Buch S. 39 Nr. 8.
Die Münze wird dreimal hintereinander geworfen. Es handelt sich also um ein mehrstufiges Zufallsexperiment (DREI STUFEN). Zeichne die Pfade (Äste) für die 1. Stufe (erster Wurf) weit auseinander, damit auch noch die Pfade für die zweite und dritte Stufe Platz haben.
Berechne dann P(W,W,W) mit der Produktregel.


Verkürzte Baumdiagramme

Video laden
YouTube


Übung 5
Löse Buch S. 47 Nr. 7 und 8.

Ein Dodekaeder ist ein Würfel mit 12 Flächen, also mit den Ziffern 1 bis 12. Die zwei Stufen des Baumdiagrammes sind der 1. Wurf und der 2. Wurf.
a) Eine Augensumme größer als 21 betrifft nur die Ergebnisse, bei denen die Würfel mindestens 10, 11 oder 12 anzeigen. Also reichen als Äste die möglichen Ausgänge 1-9, 10, 11, 12 aus. Die Wahrscheinlichkeiten sind dann für den ersten Ast und für die weiteren je .
Für das Ereignis E:"eine Augensumme größer als 21 erzielen" berechne zunächst die Wahrscheinlichkeiten der günstigen Ergebnisse (10,12), (11,11), (11,12), (12,10), (12,11), (12,12) mit der Produktregel.

Bestimme dann P(E) mit der Summenregel.

b) Für das Ereignis E:"bei höstens zwei Versuchen einmal eine 1 oder 12 werfen" ist für die Ausgänge des Würfelns nur wichtig, ob die Zahl eine 1, eine 12 oder eine 2-11 ist. Also reichen als Äste diese möglichen Ausgänge. Die Wahrscheinlichkeiten sind dann für den ersten Ast und für den zweiten Ast ebenfalls und für den letzen Ast (2-11) .
Für das Ereignis E:"bei höchstens zwei Versuchen einmal eine 1 oder 12 werfen" berechne zunächst die Wahrscheinlichkeiten der günstigen Ergebnisse (1) (2-11,1), (2-11,12), (12) mit der Produktregel.

Bestimme dann P(E) mit der Summenregel.
Für das Ereignis E:"jedes Mal eine durch 10 teilbare Zahl zu erhalten" sind die Äste mit den Ausgängen "durch 10 teilbare Zahl" und "nicht durch 10 teilbare Zahl" nötig. Der erste Ast hat dann die Wahrscheinlichkeit = , denn von den Zahlen von 1 bis 30 sind die 10,20 und 30 durch 10 teilbare Zahlen. Die Wahrscheinlichkeit des zweiten Astes beträgt dann = .
Für das Ereignis E:"eine Summe kleiner als 5 zu erzielen" sind die Ausgänge 1, 2, 3 und 4-30 wichtig. Die Ergebnisse (1,1), (1,2), (1,3), (2,1), (2,2), (3,1) sind dann die günstigen Ergebnisse für das Ereignis.


3.3 Ziehen mit und ohne Zurücklegen

Ziehen mit Zurücklegen
Urne 2rot 3 blau.png
In einer Urne befinden sich 2 rote und 3 blaue Kugeln. Es wird eine Kugel gezogen, die Farbe wird notiert und die Kugel dann zurückgelegt. Erstelle ein Baumdiagramm und beschrifte es vollständig.
a) Bestimme bestimme die Wahrscheinlichkeiten für alle möglichen Ereignisse.
b) Bestimme die Wahrscheinlichkeit für E: "eine blaue und eine rote Kugel ziehen".

Lösung:

Video laden
YouTube


Ziehen ohne Zurücklegen
Urne 2rot 3 blau.png
In einer Urne befinden sich 2 rote und 3 blaue Kugeln. Es wird eine Kugel gezogen, die Farbe wird notier und die Kugel wird NICHT zurückgelegt, sie bleibt außerhalb der Urne.Erstelle ein Baumdiagramm und beschrifte es vollständig.
a) Bestimme bestimme die Wahrscheinlichkeiten für alle möglichen Ereignisse.
b) Bestimme die Wahrscheinlichkeit für E: "eine blaue und eine rote Kugel ziehen".

Lösung:

Video laden
YouTube


Übung 6
Löse Buch S. 39 Nr. 7 und 9.
Da hier Paarungen für Fußballspiele gezogen werden, wird hier "ohne Zurücklegen" gezogen, eine Mannschaft kann nicht gegen sich selbst spielen.
Die zwei Stufen des Baumdiagramms sind der erste und zweite Zug einer Mannschaft. Die Pfade (Äste) führen jweils zu den möglichen Ausgängen Amerika, Afrika, Europa und Asien. Beachte bei der Angabe der Wahrscheinlichkeiten in der zweiten Stufe, dass "ohne Zurücklegen" gezogen wird, sich also die Wahrscheinlichkeiten im Vergleich zur ersten Stufe ändern.
Die Aufgabenteile a), b) und c) fragen nach Wahrscheinlichkeiten von Ergebnissen (geordneten Paaren), wende also die Produktregel an.

Im Aufgabenteil d) geht es um das Ereignis E:"zweite Mannschaft nicht aus Europa". Günstige Ergebnisse sind hier also (Am,...) (also (Am, Am), (Am,Af), (Am,Eu), (Am,As)), (Af,...) (also (Af,Am),(Af,Af), (Af, Eu), (Af,As)) und (As,...) (also (As,Am), (As,Af), (As,Eu), (As,As)).
Hier kannst du also kurz mit der Summmenregel rechnen:

P(E) = P(Am) + P(Af) + P(As) = + + = = = 0,6 = 60%.
Im Aufgabenteil e) geht es um das Ereignis E:"zweite Mannschaft aus Europa". Günstige Ergebnisse sind hier also (Am,Eu), (Af,Eu), (Eu,Eu) und (As,Eu). Berechne die Wahrscheinlichkeiten der Ergebnisse mit der Produktregel und dann P(E) mit der Summenregel.
Im Aufgabenteil f) geht es um das Ereignis E:"keine Mannschaft aus Europa". Günstige Ergebnisse sind hier also (Am,Am), (Am,Af), (Am,As), (Af,Am), (Af,Af), (Af,As), (As,Am), (As,Af), (As,As). Berechne die Wahrscheinlichkeiten der Ergebnisse mit der Produktregel und dann P(E) mit der Summenregel. Vergleiche dein Ergebnis: P(E) =
Du kannst die Wahrscheinlichkeit des Ereignisses E auch mithilfe des Gegenereignisses bestimmen: :"eine Mannschaft aus Europa". Hier sind die günstigen Ergebnisse (Am,Eu), (Af,Eu), (Eu), (As,Eu).
P(E) = 1 - P() = ...=

Die zwei Stufen des Experimentes sind das zweimalige Ziehen ohne Zurücklegen. Die Pfade (Äste) je Stufe führen zu den möglichen Ausgängen 0 bis 9. Da hier nur nach zwei bestimmten Ergebnissen (2,1) und (2,2) gefragt ist, reicht es aus, ein verkürztes Baumdiagramm zu zeichnen.

Zeichne in der ersten Stufe nur zwei Pfade, einen zum Ausgang "2" und den anderen zum Ausgang "nicht 2". In der zweiten Stufe zeichne drei Pfade. Den ersten zum Ausgang "1", den zweiten zu "2" und den dritten zu "nicht 1 oder 2".
Beachte bei den Wahrscheinlichkeiten für die Pfade, dass in der Lostrommel zu Beginn 20 Kugeln sind, da jede Kugel mit der Ziffer 0 bis 9 zweimal vorkommt. Im zweiten Zug sind dann nur noch 19 Kugeln insgesamt vorhanden, da ohne Zurücklegen gezogen wird.
Bestimme die Wahrscheinlichkeit in Aufgabe a) die Zahl 21 zu ziehen, indem du P(2,1) mithilfe der Produktregel berechnest. Bei Aufgabe b) bestimme P(2,2) mit der Produktregel.


Übung 7
Löse Buch S. 40 Nr. 12, 13 und 14.
Um welche zwei Stufen handelt es sich jeweils beim Experiment? Verändern sich die Wahrscheinlichkeiten in der zweiten Stufe?
Wenn du "mit einem Griff" zwei Lose ziehst, handelt es sich um ein Ziehen ohne Zurücklegen, da du nicht zweimal dasselbe Los ziehen kannst.


NÄCHSTES KAPITEL: ERWARTUNGSWERT

Video laden
YouTube


Video laden
YouTube
Abgerufen von „https://projekte.zum.de/index.php?title=Buss-Haskert/Zweistufige_Zufallsexperimente/Zweistufige_Zufallsexperimente&oldid=33621“