Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Die Steigung in einem Punkt - die Ableitung als Tangentensteigung

Inhaltsübersicht

a) Unterscheidung Tangente, Sekante und Normale - Aufgabe 1
b) Zuordnungsaufgaben bezüglich der Tangentensteigung - Aufgabe 2, 3, 4 und 5
c) Untersuchung einer Funktion - Aufgabe 6, 7, 8 und 9

a) Unterscheidung Tangente, Sekante und Normale

Aufgabe 1

Kannst du die Begriffe unterscheiden?

b) Zuordnungsaufgaben bezüglich der Tangentensteigung

Aufgabe 2

Ordne die jeweilige Steigung den entsprechenden Punkten zu.

Aufgabe 3

Die Steigung der Tangente in einem x-Wert

Aufgabe 4

Wahr oder Falsch?

Aufgabe 5

Gehört es zur Sinuskurve oder nicht?

Error: www.geogebra.org is not an authorized iframe site.

c) Untersuchung einer Funktion

Aufgabe 6

Steigung und Koordinaten ablesen

Aufgabe 7

Raupenfahrt

<popup name="Lösung"> Die Steigfähigkeit der Raupe liegt mit 76% über der Steigung von 75%. </popup>

Aufgabe 8*

Kann es in einem Punkt einer Funktion zwei oder mehr Tangenten geben?!
Luis und Marie sind sich uneinig. Beide schauen sich den untenstehenden Graphen an.
Luis sagt: "Wenn ich mir die Steigung im Punkt P(6/6)anschauen, sehe ich zwei Tangenten."

Marie entgegnet: "Also ich sehe da überhaupt keine Tangente. Da kann gar keine sein!"

a) Überleg dir, welche zwei Tangenten Luis meint und warum?
Denkst du es gibt hier eine Tangente oder sogar mehrere?
Zeichne Luis` Tangenten mit dem Graphen in dein Heft und ergänze ggf. deine Tangente(n).

Error: www.geogebra.org is not an authorized iframe site.

<popup name="Hinweis zu a)">

Hast du dir wirklich Gedanken gemacht?

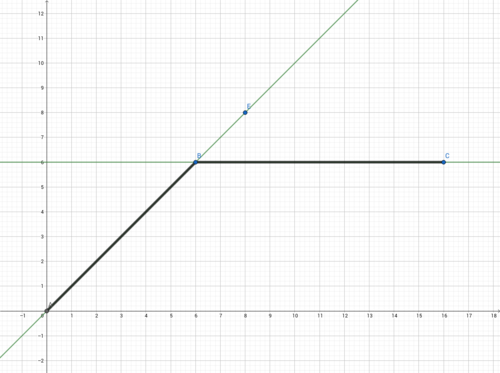
<popup name="Hinweis a)"> Luis betrachtet die Steigung im Punkt P(6|6).
Dabei schaut er sich die Steigung links und rechts von P an.

</popup>

<popup name="Lösung a)">

Luis hat sich überlegt, wie die Steigung links und rechts vom Punkt P(6|6) ist. Falls es jedoch eine Steigung in einem Punkt einer Funktion gibt, so muss diese eindeutig sein.
Ansonsten ist die Funktion nicht differenzierbar.

</popup>

b) Zeichne die Steigung der Funktion in dein Heft. Du kannst dich auf die Intervalle [0;6] und [6;12] beschränken. Wie verläuft die Steigung und was passiert im Punkt P(6|6)?

<popup name="Lösung b)"> Die Steigung verläuft im Intervall [0;6] und [6;12] linear. Jedoch gibt es im Punkt P(6|6) einen Sprung.
Hier ist die Ableitung also nicht stetig (zusammenhängend) und daher im Intervall [0;12] nicht differenzierbar, wie oben schon zu sehen war.
Damit du die Ableitung in einem Punkt berechnen kannst, muss die Funktion dort auch differenzierbar sein.

Error: www.geogebra.org is not an authorized iframe site.

</popup>