Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Von der mittleren zur momentanen (lokalen) Änderungsrate: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Main>Lena WWU
Keine Bearbeitungszusammenfassung
Main>Lena WWU
Keine Bearbeitungszusammenfassung
Zeile 1: Zeile 1:
__TOC__
__TOC__
==Aufgabe 1: Die durchschnittliche Änderungsrate ==
 
====Wie groß ist die durchschnittliche Änderung für...====
==Die durchschnittliche Änderungsrate ==
{{Aufgaben|1a: Wie groß ist die durchschnittliche Änderung für...|
# <math>f(x)=x^2 </math> im Intervall <math>[3, 5]</math> und im Intervall <math>[-1, 1]</math>
# <math>f(x)=x^2 </math> im Intervall <math>[3, 5]</math> und im Intervall <math>[-1, 1]</math>
# <math>g(x)=1-x^2</math> im Intervall <math>[1, 3]</math>
# <math>g(x)=1-x^2</math> im Intervall <math>[1, 3]</math>
# <math>h(x)=-\frac{1}{8}x^2+2x</math> im Intervall <math>[2, 10]</math>
# <math>h(x)=-\frac{1}{8}x^2+2x</math> im Intervall <math>[2, 10]</math>
# <math>i(x)=x^3+4x</math> im Intervall <math> [-5, 6]</math>
# <math>i(x)=x^3+4x</math> im Intervall <math> [-5, 6]</math>
# <math>j(x)=x^4+2x^2-x</math> im Intervall <math>[-6, -2]</math> ?
# <math>j(x)=x^4+2x^2-x</math> im Intervall <math>[-6, -2]</math> ?}}




Zeile 19: Zeile 20:
<iframe width="560" height="315" src="https://www.youtube.com/embed/IuaWZ6CLniM" frameborder="0" gesture="media" allowfullscreen></iframe>
<iframe width="560" height="315" src="https://www.youtube.com/embed/IuaWZ6CLniM" frameborder="0" gesture="media" allowfullscreen></iframe>
</popup>
</popup>
====Das Wetter in Münster und Lumbashi====
 
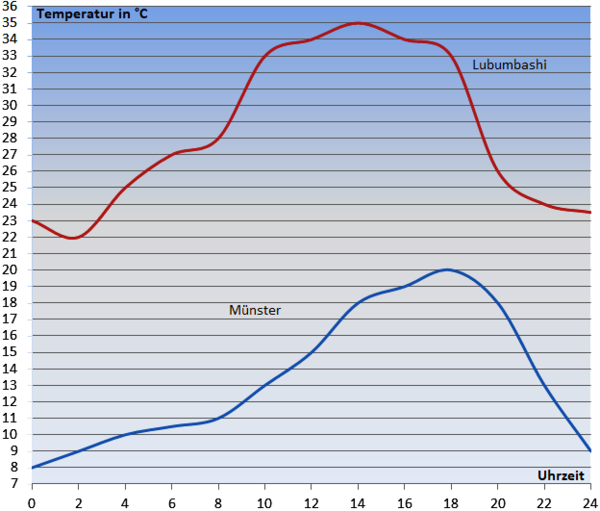
{{Aufgaben|1b: Das Wetter in Münster und Lumbashi|
 
[[Datei:Temperaturkurve, Münster, Lubumbashi.png|thumb|Temperature curve, Münster, Lubumbashi|zentriert|600px]]
[[Datei:Temperaturkurve, Münster, Lubumbashi.png|thumb|Temperature curve, Münster, Lubumbashi|zentriert|600px]]
<iframe src="https://learningapps.org/watch?v=pxdjxcp5c17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
<iframe src="https://learningapps.org/watch?v=pxdjxcp5c17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>}}


==Aufgabe 2: Unterscheidung von durchschnittlicher und momentaner Änderungsrate==
==Unterscheidung von durchschnittlicher und momentaner Änderungsrate==


=Aufgabe 2a: Entscheidungen im Kontext treffen=
{{Aufgaben|2a: Entscheidungen im Kontext treffen|
<iframe src="https://learningapps.org/watch?v=p35kyu2yj17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
<iframe src="https://learningapps.org/watch?v=p35kyu2yj17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>}}


<popup name="Hilfestellung 1">
<popup name="Hilfestellung 1">
Zeile 35: Zeile 38:
{{#ev:youtube|https://youtu.be/bd8Lao_ZWo8}}
{{#ev:youtube|https://youtu.be/bd8Lao_ZWo8}}
</popup>
</popup>
=Aufgabe 2b: Reflexion der Entscheidungen=
 
Formuliere in deinem Heft, woran du die Entscheidung für die momentane oder durchschnittliche Änderungsrate festmachst!
{{Aufgaben|2b: Reflexion der Entscheidungen
Formuliere in deinem Heft, woran du die Entscheidung für die momentane oder durchschnittliche Änderungsrate festmachst!}}
<popup name="Lösung">
<popup name="Lösung">
Im Kontext der verstrichenen Zeit in Abhängigkeit einer anderen Größe muss die '''momentane Änderungsrate''' angewendet werden, wenn es sich um einen '''Zeitpunkt''' handelt. Bei einer '''Zeitspanne''' wird die '''durchschnittliche Änderungsrate''' benötigt.
Im Kontext der verstrichenen Zeit in Abhängigkeit einer anderen Größe muss die '''momentane Änderungsrate''' angewendet werden, wenn es sich um einen '''Zeitpunkt''' handelt. Bei einer '''Zeitspanne''' wird die '''durchschnittliche Änderungsrate''' benötigt.
</popup>
</popup>


==Aufgabe 3: Von der durchschnittlichen zur momentanen Änderungsrate - eine Fahrradtour durch Münster==
==Von der durchschnittlichen zur momentanen Änderungsrate - eine Fahrradtour durch Münster==
{{Aufgaben|3: Fahrradfahren durch Münster|
Eine Gruppe Touristen macht eine Sightseeing-Tour mit dem Fahrrad durch Münster. Weil an dem Tag Kirmes ist, können sie nicht direkt vor das Schloss fahren. Nach einem Fotostop am Schloss gehen sie zu ihren Fahrrädern zurück und fahren weiter zum Dom.
Eine Gruppe Touristen macht eine Sightseeing-Tour mit dem Fahrrad durch Münster. Weil an dem Tag Kirmes ist, können sie nicht direkt vor das Schloss fahren. Nach einem Fotostop am Schloss gehen sie zu ihren Fahrrädern zurück und fahren weiter zum Dom.
{{#ev:youtube|https://youtu.be/APDdi1Z9LQw}}
{{#ev:youtube|https://youtu.be/APDdi1Z9LQw}}
Zeile 63: Zeile 68:
</div>
</div>
:e) Wie schnell sind die Touristen beim Abbiegen von der Straße auf den Rad- und Fußgängerweg vor der eingerüsteten Überwasserkirche? Nutze dafür den Schieberegler. Das Applet stellt nur das Abbiegen dar, wobei auf der x-Achse die Zeit in Sekunden und auf der y-Achse die zurückgelegte Strecke in Metern eingetragen ist.
:e) Wie schnell sind die Touristen beim Abbiegen von der Straße auf den Rad- und Fußgängerweg vor der eingerüsteten Überwasserkirche? Nutze dafür den Schieberegler. Das Applet stellt nur das Abbiegen dar, wobei auf der x-Achse die Zeit in Sekunden und auf der y-Achse die zurückgelegte Strecke in Metern eingetragen ist.
<iframe scrolling="no" title="Das Abbiegen der Fahrradtouristen" src="https://www.geogebra.org/material/iframe/id/Q7wfvMNB/width/600/height/500/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/false/ctl/false" width="600px" height="500px" style="border:0px;"> </iframe>
<iframe scrolling="no" title="Das Abbiegen der Fahrradtouristen" src="https://www.geogebra.org/material/iframe/id/Q7wfvMNB/width/600/height/500/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/false/ctl/false" width="600px" height="500px" style="border:0px;"> </iframe>}}
<popup name="Hinweis zu 3a">
<popup name="Hinweis zu 3a">
Die Zeitangaben sind hier nicht eindeutig. Ob du denkst, dass die Radfahrer schon eine Sekunde früher oder später an einem Ort angekommen sind, ist auch nicht wichtig.
Die Zeitangaben sind hier nicht eindeutig. Ob du denkst, dass die Radfahrer schon eine Sekunde früher oder später an einem Ort angekommen sind, ist auch nicht wichtig.

Version vom 6. November 2017, 15:54 Uhr

Die durchschnittliche Änderungsrate

Aufgabe 1a: Wie groß ist die durchschnittliche Änderung für...
  1. im Intervall und im Intervall
  2. im Intervall
  3. im Intervall
  4. im Intervall
  5. im Intervall  ?


<popup name="Hilfe 1">

Differenzenquotient? Was war das denn nochmal?

Der Quotient wird Differenzenquotient genannt. Geometrisch gedeutet ist dieser Quotient die Steigung der Geraden (Sekante)durch die Punkte und . </popup>

<popup name="Hilfe 2"> </popup>


Aufgabe 1b: Das Wetter in Münster und Lumbashi


Temperature curve, Münster, Lubumbashi


Unterscheidung von durchschnittlicher und momentaner Änderungsrate

Aufgabe 2a: Entscheidungen im Kontext treffen


<popup name="Hilfestellung 1"> Überlege, ob bei der momentanen Änderungsrate (bzw. durchschnittlichen Änderungsrate) eine Stelle oder ein Intervall beschrieben wird. </popup> <popup name="Weitere Hilfestellung 2"> In diesem Video wird noch einmal am Beispiel der Geschwindigkeit erläutert, wie die Entscheidung zwischen momentaner Änderungsrate und durchschnittlicher Änderungsrate zu treffen ist:

Video laden
YouTube

</popup>


Aufgabe 2b: Reflexion der Entscheidungen Formuliere in deinem Heft, woran du die Entscheidung für die momentane oder durchschnittliche Änderungsrate festmachst!
{{{2}}}

<popup name="Lösung"> Im Kontext der verstrichenen Zeit in Abhängigkeit einer anderen Größe muss die momentane Änderungsrate angewendet werden, wenn es sich um einen Zeitpunkt handelt. Bei einer Zeitspanne wird die durchschnittliche Änderungsrate benötigt. </popup>

Von der durchschnittlichen zur momentanen Änderungsrate - eine Fahrradtour durch Münster

Aufgabe 3: Fahrradfahren durch Münster
{{{2}}}

<popup name="Hinweis zu 3a"> Die Zeitangaben sind hier nicht eindeutig. Ob du denkst, dass die Radfahrer schon eine Sekunde früher oder später an einem Ort angekommen sind, ist auch nicht wichtig. </popup> <popup name="Hinweis zu 3b"> Achte genau auf die Einheiten! </popup> <popup name="Hilfe zu 3b"> Meter pro Sekunde (m/s) kannst du in Kilometer pro Stunde (km/h) umrechnen, in dem du einzeln die Meter in Kilometer und die Sekunden in Stunden umrechnest. </popup>

Abgerufen von „https://projekte.zum.de/index.php?title=Digitale_Werkzeuge_in_der_Schule/Ableitungen_üben_und_vertiefen/Von_der_mittleren_zur_momentanen_(lokalen)_Änderungsrate&oldid=3014“