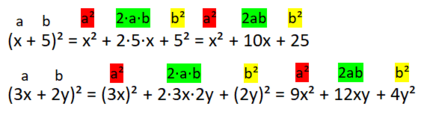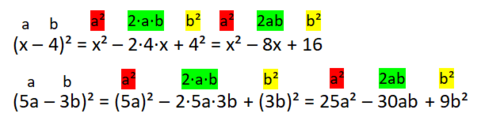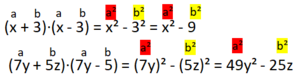Benutzer:Buss-Haskert/Terme(mit Klammern)/Binomische Formeln

zurück zur Startseite

3. Binomische Formeln

Die binomische Formeln sind drei Sonderfälle bei der Multiplikation von Summen. Die Ergebnisse lassen sich hier leicht zusammenfassen und so die ausführlichen Berechnungen abkürzen.

Durch entsprechende Figuren lassen sie sich auch gut anschaulich erklären.

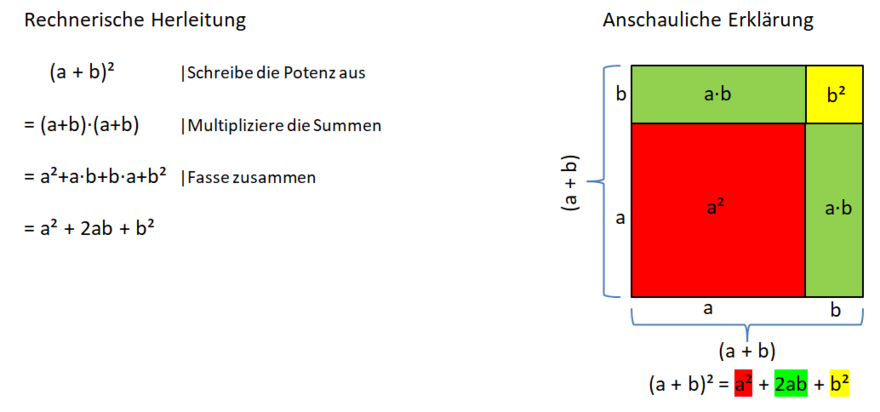
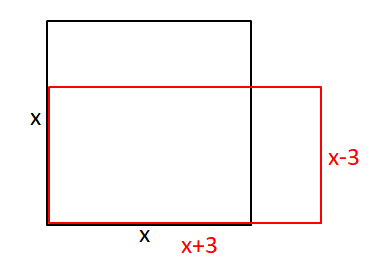
1. binomische Formel

Herleitung der 1. binomischen Formel

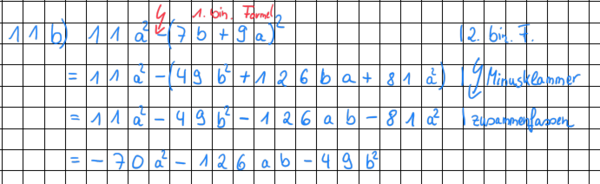
Beispiele:

1. binomische Formel

Übertrage die Herleitung und die Beispiele in dein Heft.      
(a+b)²=a²+2ab+b²

Übung 1

Übung 1

Bearbeite die nachfolgenden LearningApps.

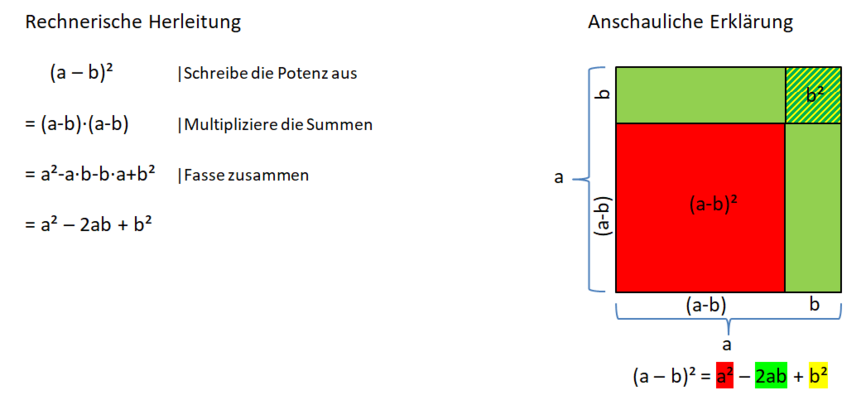
2. binomische Formel

Herleitung der 2. binomischen Formel

Das GeoGebra-Applet leitet anschaulich die 2. binomische Formel her. Erkläre deinem Partner die einzelnen Schritte.

Beispiele:

2. binomische Formel

Übertrage die Herleitung und die Beispiele in dein Heft.
(a-b)²=a²-2ab+b²

Übung 2

Übung 2

Bearbeite die nachfolgenden LearningApps.

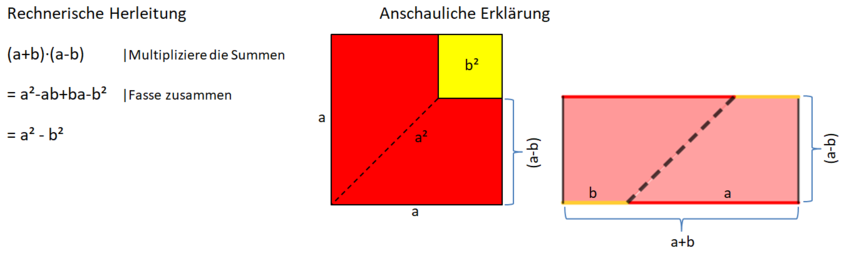
3. binomische Formel

Herleitung der 3. binomischen Formel

Das GeoGebra-Applet leitet anschaulich die 3. binomische Formel her. Erkläre deinem Partner die einzelnen Schritte.

Beispiele:

3. binomische Formel

Übertrage die Herleitung und die Beispiele in dein Heft.
(a+b)(a-b) = a² - b²

Übung 3

Übung 3

Bearbeite die nachfolgenden LearningApps.

hier noch ergänzen!

Zusammenfassung

Das nachfolgende Video fasst die binomischen Formeln noch einmal zusammen.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Nun hast du alle drei binomischen Formeln kennengelernt. Höre das Lied dazu an, dann kannst du dir die Formeln gut merken (es ist ein Ohrwurm).

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Vermischte Übungen zu den binomischen Formeln?

Übung 4

Übung 4

Bearbeite die nachfolgenden LearningApps und Quizze.

Übung 5

Übung 5

Löse Buch S. 16 Nr. 6, 7, 9 und 11. Notiere deine Rechnungen in dein Heft.

Löse Nr. 11 schrittweise:

Wende zuerst die binomischen Formeln an. Prüfe dann, ob zum Auflösen der Klammer noch ein weitere Schritt notwendig ist (wenn z.B. ein Minuszeichen vor der Klammer steht). Fasse danach zusammen.

Übung 6 Quadratzahlen und besondere Produkte mit den binomischen Formeln berechnen

Die 1. und 2. binomische Formel helfen beim Berechnen von größeren Quadratzahlen.

Berechnung von Quadratzahlen mit binomische Formeln

Schreibe die Beispiele unten in dein Heft. Erkläre, wie die binomischen Formeln dir beim Rechnen helfen. Wann wendest du die 1., die 2. oder die 3. binomische Formel an?

Beispiele:
46² = (40+6)²
  =40² + 2∙40∙6 + 6²
  =1600 + 480 + 36
  =2116

39² = (40-1)²
  =40² - 2∙40∙1 + 1²
  =1600 - 80 + 1
  =1521

63 ∙ 57 = (60+3)∙(60-3)
  =60² - 3²
  =3600 - 9
  =3591

Übung 7 Anwendungsaufgabe: Grundstückstausch

Grundstückstausch

Frau Müller besitzt ein quadratisches Grundstück. Dort soll eine Straße gebaut werden. Man bietet ihr zum Tausch ein rechteckiges Grundstück an. Das ist auf der einen Seite 3m kürzer und zum Ausgleich auf der anderen Seite 3m länger als ihr bisheriges Grundstück. Ist dieser Tausch fair?

Benenne die Länge des quadratischen Grundstückes mit x.
Nun hilft eine Skizze:

Schau das Video an und übertrage die Idee auf die Aufgabe.Vorlage:Ev:youtube

4. Binomische Formeln "rückwärts" - Faktorisieren mit binomischen Formeln

Du kannst bestimmte Summen mithilfe der binomischen Formeln in ein Produkt verwandeln. Dazu müssen die Summen die Form einer binomischen Formel haben.

Üben

Gib die folgenden Summen als Produkte an:
a) a² + 2ab + b² = (.....)²        x² + 18x + 81 = (......)²
b) a² - 2ab + b² = (......)²       64x² - 48xy + 9y² = (......)²
c) a² - b² = (....)·(....)       4x² - 121y² = (...)·(...)

Wie gehst du vor? Erkläre!

Erinnerung: a²+2ab+b²=(a+b)² Hier handelt es sich auf der linken Seite um den Summenterm der 1. binomische Formel, also muss das Produkt (a+b)(a+b) heißen, bzw. kurz (a+b)².

Ebenso ist x² + 18x + 81 der Summenterm von (x+3)², denn (x+9)² = x² + 2·x·9 + 9² = x² + 18x + 81. Du musst also die 1. binomische Formel "rückwärts" anwenden.

Erinnerung: a²-2ab+b²=(a-b)² Hier handelt es sich auf der linken Seite um den Summenterm der 2. binomische Formel, also muss das Produkt (a-b)(a-b) heißen, bzw. kurz (a-b)².

Ebenso ist 64x² - 48xy + 9y² der Summenterm von (8x-3y)², denn (8x-3y)² = (8x)² + 2·8x·3y + (3y)² = 64x² + 48xy + 9y². Du musst also die 2. binomische Formel "rückwärts" anwenden.

Erinnerung: a² - b² = (a+b)(a-b)= a² - b². Hier handelt es sich auf der linken Seite um den Summenterm der 3. binomische Formel, also muss das Produkt (a+b)(a-b) heißen.

Ebenso ist 4x² - 121y² der Summenterm von (2x+11y)(2x-11y), denn (2x+11y)(2x-11y) =(2x)² - (11y)² = 4x² - 121y². Du musst also die 3. binomische Formel "rückwärts" anwenden.

zurück zur Startseite