Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der durchschnittlichen zur lokalen Änderungsrate: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 228: | Zeile 228: | ||
''''' | ''''' | ||
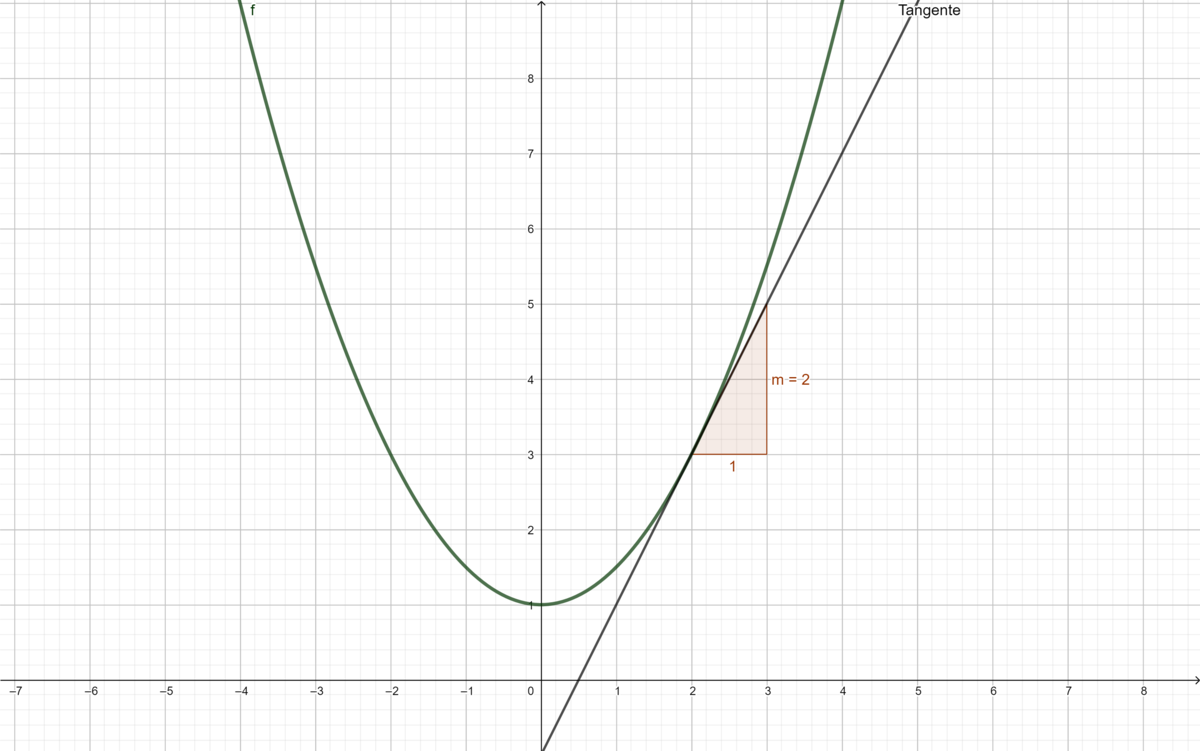
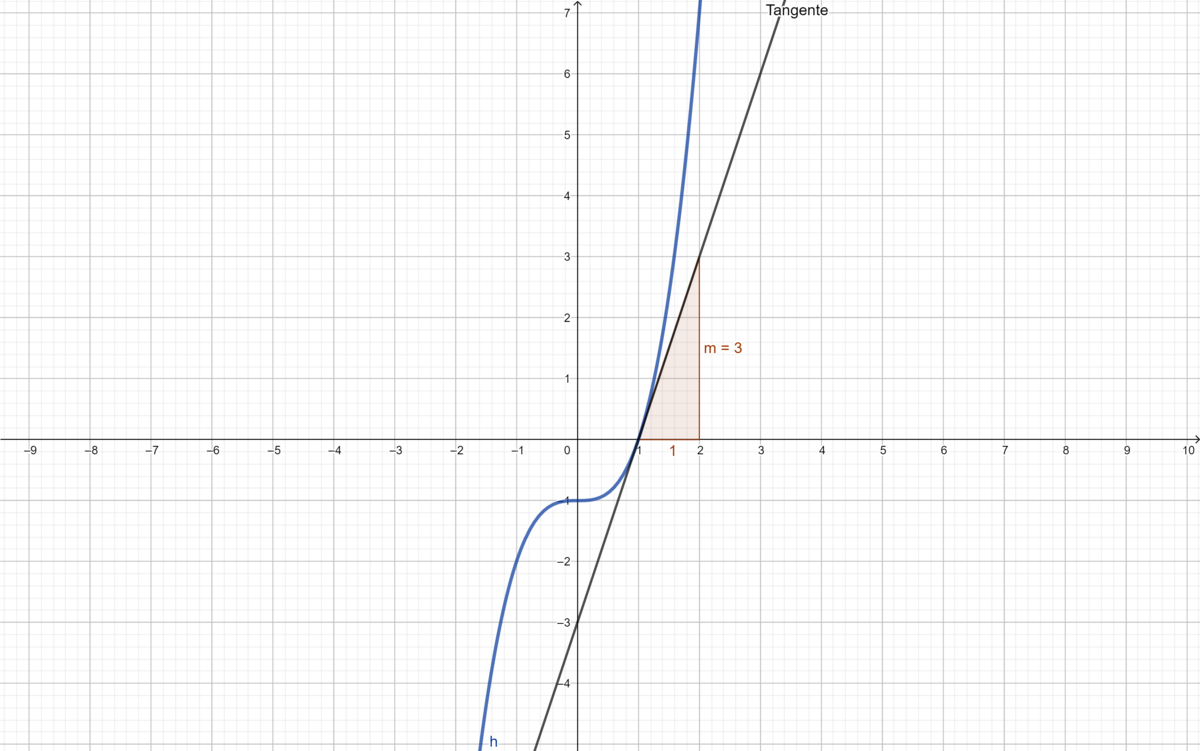
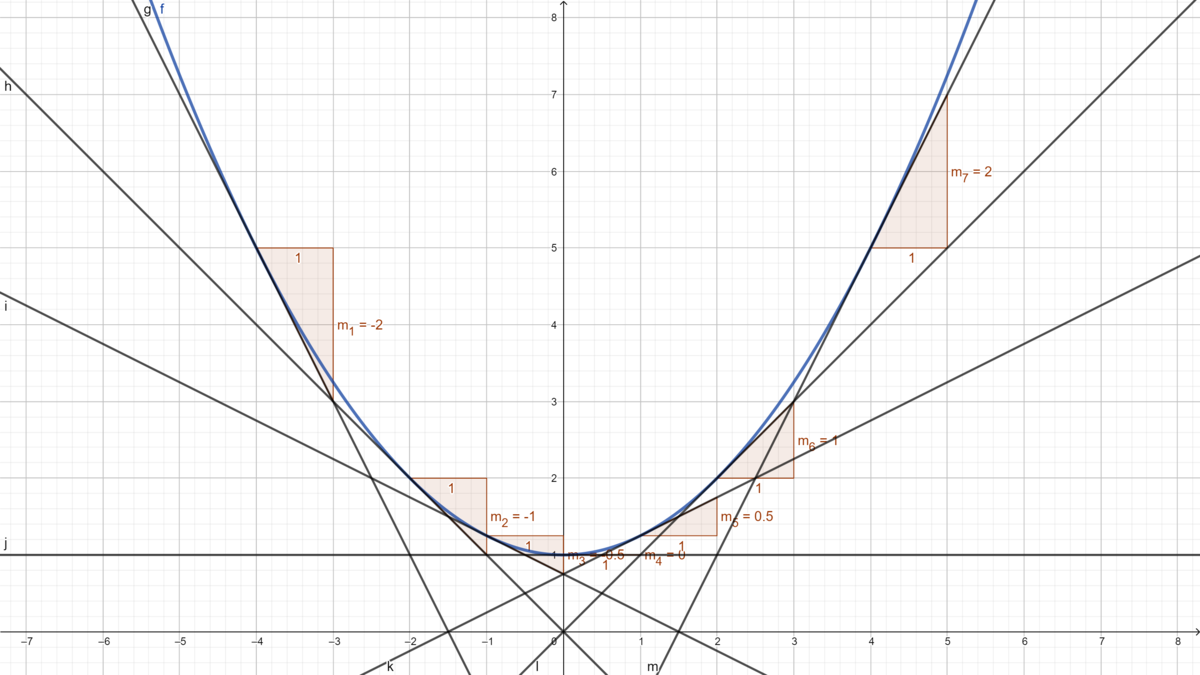
{{Lösung versteckt|1= Für alle Wertepaare gilt, dass der Wert <math>m</math> ein Vielfaches von <math>x</math> ist, wobei dieser Faktor eine feste Zahl ist. Solche Zuordnungen nennt man linear.|2=Tipp|3=Tipp}} | {{Lösung versteckt|1= Für alle Wertepaare gilt, dass der Wert <math>m</math> ein Vielfaches von <math>x</math> ist, wobei dieser Faktor eine feste Zahl ist. Solche Zuordnungen nennt man linear.|2=Tipp|3=Tipp}} | ||
{{Lösung versteckt|1 = Die Funktionsgleichung lautet: <math>m(x) = \tfrac{1}{2} x</math>. Denn <math>-1 = 0,5 \cdot (-2) | {{Lösung versteckt|1 = Die Funktionsgleichung lautet: <math>m(x) = \tfrac{1}{2} x</math>. Denn <math>-1 = 0,5 \cdot (-2)</math> oder <math>1,5 = 0,5\cdot 3</math>. Diese Funktion gibt die lokale Steigungsänderung der Achterbahn in Abhängigkeit von dem Streckenpunkt. Dieses Verfahren nennt man graphisches Differenzieren und die Funktion ist die Ableitungsfunktion von <math>f(x)</math>. Im Teil c) kannst du diese Behauptung rechnerisch überprüfen.|2= Lösung|3=Lösung}} | ||
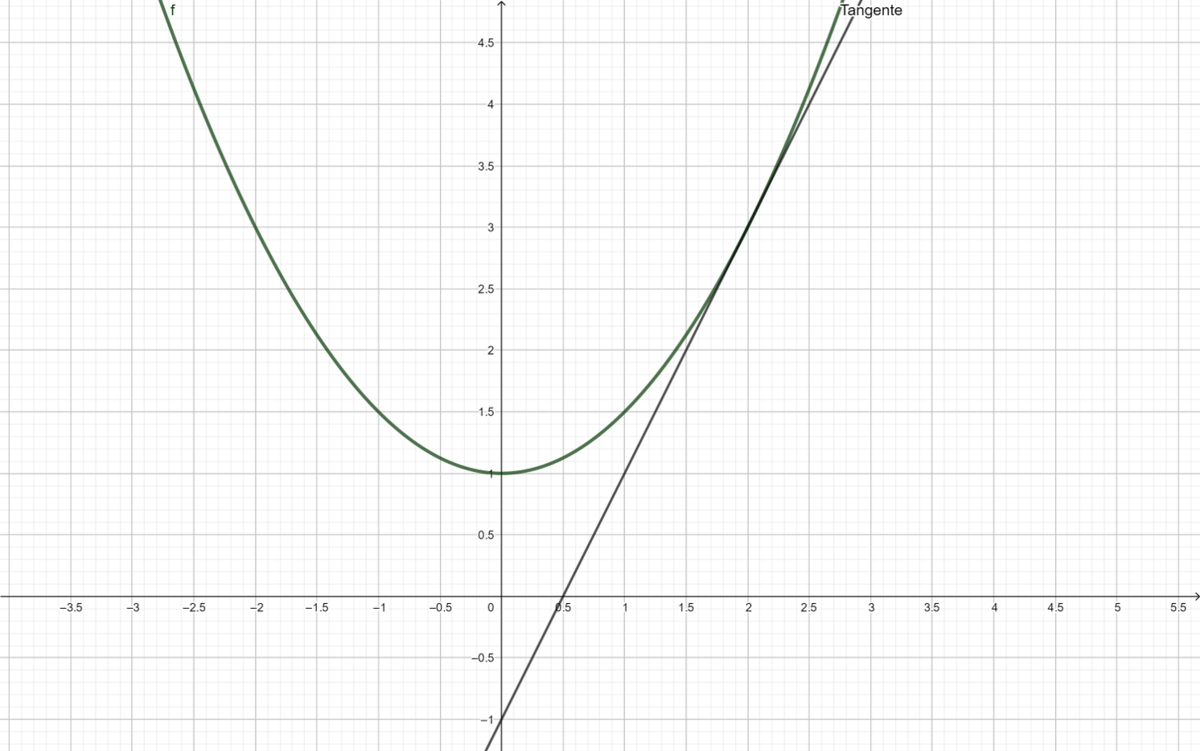
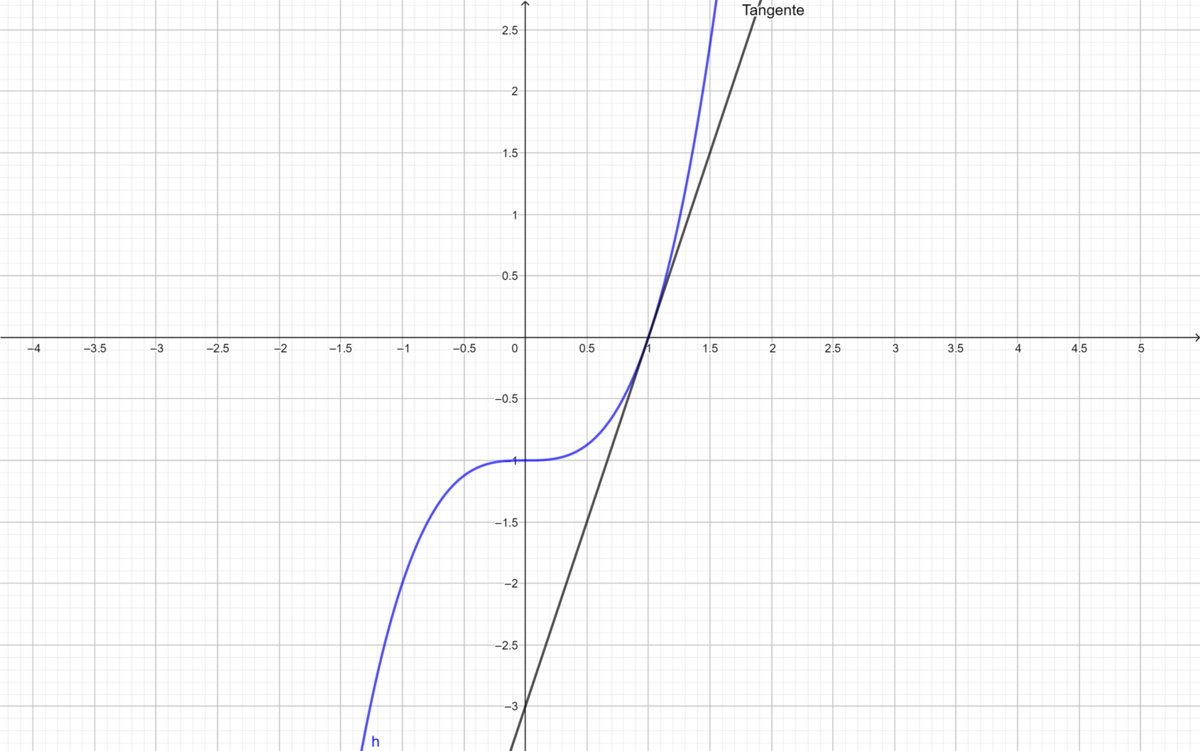
'''''c) Berechne den Differentialquotienten von <math>f(x) = \tfrac{1}{4} x^2 + 1 </math>in einem beliebigen Punkt. Vergleiche dein Ergebnis mit dem Ergebnis von Teil b).''''' | '''''c) Berechne den Differentialquotienten von <math>f(x) = \tfrac{1}{4} x^2 + 1 </math>in einem beliebigen Punkt. Vergleiche dein Ergebnis mit dem Ergebnis von Teil b).''''' | ||
Version vom 25. Mai 2020, 16:55 Uhr
Grundlegende Begriffe und Formeln
Aufgaben zum Wiederholen und Vertiefen
Mittelschwere Aufgaben
Knobelaufgaben