Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der durchschnittlichen zur lokalen Änderungsrate

Info

Dieses Lernpfadkapitel bietet dir einen Einstieg in das Thema Differenzialrechnung. Nach der Bearbeitung des Kapitels kannst du die Formeln für beide Änderungsraten angeben und anwenden, die Änderungsraten in unterschiedlichen sachlichen Anwendungen berechnen und den Zusammenhang zwischen Sekanten- und Tangentensteigung erläutern. Zuerst erklären wir dir wichtige Begriffe und Zusammenhänge. Danach kannst du selbständig die Aufgaben bearbeiten. Du benötigst Papier und Stifte, Lineal und Taschenrechner. Die Aufgaben haben 3 unterschiedliche Schwierigkeitsstufen, die farblich gekennzeichnet sind:

In Aufgaben, die orange gefärbt sind, kannst du Gelerntes wiederholen und vertiefen

Aufgaben, die blauen Farbe sind Aufgaben mittlerer Schwierigkeit

Und Aufgaben mit grüner Hinterlegung sind Knobelaufgaben, dabei sind die Aufgaben für den LK mit einem ⭐ gekennzeichnet.

Viel Erfolg und viel Spaß!

Grundlegende Begriffe und Formeln

Beschreibung von Änderungsprozessen mit Änderungsraten

Der Niagara River verbindet den Eriesee mit dem Ontariosee, in den Horseshoe Falls stürzt er 57m in die Tiefe. Der Graph (schwarz) simuliert den Fall eines Steins von der Kante des Wasserfalls. Die durchschnittliche Fallgeschwindigkeit ist die Veränderung der Höhe in einem Zeitabschnitt. Verschiebe den Regler und beobachte, wie sich die durchschnittliche Geschwindigkeit verändert. Mathematisch gesehen ist die Fallgeschwindigkeit in einem Zeitabschnitt die durchschnitlliche Änderungsrate der Funktion in einem Intervall. Du ermittelst diese als Steigung der Sekante (rote Linie) zwischen 2 Punkten.

Wie schnell ist der Stein beim Aufprall auf die Wasseroberfläche? Verschiebe den Regler ganz nach rechts, aus dem Zeitintervall wird ein Zeitpunkt. Die rote Linie berührt den Graph und in diesem Punkt stimmen die Steigung des Graphen und die Steigung der roten Linie (Tangente) lokal nahezu überein. Die Steigung der Tangente beschreibt das Verhalten der Funktion im Berührungspunkt und wird als lokale Änderungsrate bezeichnet. In unserem Fall ist es die momentane Geschwindigkeit beim Aufprall.

Merke

Die durchschnittliche Änderungsrate einer Funktion $f(x)$ bezieht sich immer auf ein bestimmtes Intervall $[x_1, x_2]$ und wird mit Hilfe des Differenzenquotienten berechnet:

$\frac{f(x_2) - f(x_1)}{x_2 - x_1} = \frac{\bigtriangleup f(x)}{\bigtriangleup x}$

Merke

Die lokale Änderungsrate in einem Punkt nennt man Differenzialquotient oder Ableitung in einem Punkt und berechnet diesen als Grenzwert (du schreibst dafür $\lim$ ) der Sekantensteigungen:

$f'(x)=\lim_{x_2 \to \ x_1}\frac{f(x_2)-f(x_1)}{x_2-x_1}$

Setzt man $h$ für den Abstand von $x_2$ zu $x_1$ so gilt die Formel:

$f'(x)=\lim_{h \to \ 0}\frac{f(x+h)-f(x)}{h}$

Aufgaben zum Wiederholen und Vertiefen

Aufgabe 1: Durchschnittliche Änderungsrate berechnen

Bestimme die durchschnittlichen Änderungsraten der Funktionen in den vorgegebenen Intervallen. Du benötigst für die Aufgabe Papier, Stifte und evtl. einen Taschenrechner.

a) $f(x) = \tfrac{1}{2}x^2 - \tfrac{3}{2}$ in dem Intervall [1; 2]

Die durchschnittliche Änderung auf dem Intervall beträgt $\tfrac{3}{2}$.

Setze die Werte wie folgt in die Formel ein: $\frac{f(2) - f(1)}{2-1} = \frac{\frac{1}{2}-(-1)}{2-1} = \frac{3}{2}$

b) $g(x) = x^3 - 0,2x - 3$ in dem Intervall [-2; -1]

Die durchschnittliche Änderung auf dem Intervall beträgt 6,8.

Wie komme ich zu meiner Lösung? Setze die Werte wie folgt in die Formel ein: $\frac{g(-1) - g(-2)}{-1-(-2)} = \frac{-3,8-(-10,6)}{-1-(-2)} = 6,8$

c) $h(x) = \tfrac{1}{4}x^2$ in dem Intervall [1,99; 2,01] Überlege, was in dem Intervall mit der Sekante passiert.

Die durchschnittliche Änderung auf dem Intervall beträgt 1.

Setze die Werte wie folgt in die Formel ein: $\frac{h(2,01) - h(1,99)}{2,01-1,99} = \frac{1,010025-0,990025}{2,01-1,99} = 0,02:0,02 = 1$.

Da das Intervall sehr klein ist, nähern sich die Schnittpunkte der Sekante mit der Funktion und die durchschnittliche Änderungsrate geht in die lokale über.

Für die Berechnung der durchschnittlichen Änderungsrate schau dir die Formel in dem ersten Merkkasten an. Für $x_1$ und $x_2$ setze die Intervallgrenzen ein. Z.B. 2 und 3 für das Intervall [2;3]

Aufgabe 2: Übergang von durchschnittlicher zur lokaler Änderungsrate

Du benötigst für diese Aufgabe Papier und Stifte für Notizen.

In dem Applet ist der Graph der Funktion $f(x)=0,1\cdot x^2 +1$ dargestellt.

• a) Verändere mithilfe des Schiebereglers für Δx den Abstand zwischen den Punkten A und B und notiere für

Δx = 3.5 ; 3.0 ; 2.5; 2.0; 1.5; 1.2; 1.1 und 0.5 die Steigung k der Sekanten durch die Punkte A und B.

• b) Kannst du damit die Steigung der Tangente, also die lokale Änderungsrate an einem Punkt ermitteln?

Schiebe den Regler so weit, dass Δx=0 ist. Die Schnittpunkte nähern sich also, die Sekante geht in die Tangente über und somit entsteht aus der durchschnittlichen Änderungsrate am Grenzübergang die lokale.

• c) Führe dieselbe Aufgabe für die Funktion $f(x) =0,1 \cdot x^2$ durch. Was stellst Du fest? Ist es überraschend?

Die Steigung der Tangenten beider Funktionen beträgt im Punkt A $m=0,6$. Die notierten Werte der durchschnittlichen Änderungsraten nähern sich dieser Zahl an, wenn das Intervall Δx sich der Zahl 0 nähert. Das entspricht genau der Definition der Tangente als Grenzwert der Sekantensteigungen. Der gleiche Wert für die zweite Funktion sollte auch nicht überraschen, denn diese ist die gleiche Funktion, lediglich um 1 nach unten verschoben.

Aufgabe 3: Schlittenfahrt

Im kalten Winter unter idealen Bedingugnen (keine Reibung, kein hektisches Lenken und kein unnötiges Bremsen) schlitterst Du einen Hang mit 5% Gefälle hinab.

Der von deinem Schlitten zurückgelegte Weg wird annähernd durch die Funktion $w(t) = \tfrac{1}{4}t^2$ beschrieben. Dabei steht $t$ für die Zeit nach dem Start in Sekunden und $w(t)$ für die seit dem Start zurückgelegte Strecke in Metern. 100m weit von deinem Startpunkt entfernt steht auf der Schräge dein Freund.

a) Wann fährst du an deinem Freund vorbei?

Hier musst du mit dem Funtkionsterm arbeiten. Die Entfernung bis zu deinem Freund, also die 100m ist der Wert der Funktion zum gesuchten Zeitpunkt $t$. Stelle mit Hilfe des Funktionsterms eine Gleichung auf, mit $t$ als Variable.

$100 = \tfrac{1}{4}t^2$

$\Leftrightarrow$$t^2 = 100 \cdot 4$

$\Leftrightarrow$$t= \pm 20$

Den Wert t = -20 können wir in dem Sachzusammenhang verwerfen (Du sitzt schließlich auf dem Schlitten, nicht in der Zeitmaschine), also fährst du 20s später an deinem Freund vorbei.

b) Welche Geschwindgkeit hat dein Schlitten zu diesem Zeitpunkt?

Die Geschwindigkeit wird als $\frac{Strecke}{Zeit}$ berechnet. Die Geschwindigkeit steht also in dieser Aufgabe für die Änderungsrate. Überlege zuerst nach welcher Änderungsrate wird hier gefragt und wende die entsprechende Formel an. Die Begriffe Strecke oder Zeitabschnitt stehen für durchschnittliche Veränderungen, dagegen wird mit Begriffen wie "zum Zeitpunkt" oder "im Moment" lokale Änderungsrate bezeichnet.

Du fährst mit einer Geschwindigkeit von 10 m/s an deinem Freund vorbei. Im Teil a) hast du berechnet, dass du nach 20s an deinem Freund vorbei schlitterst. Es gibt nun 2 Möglichkeiten die Geschwindigkeit an dieser Stelle zu berechnen.

Berechne den Differentialquotient im $t= 20$. Die Formel dazu findest du im zweiten Merkkasten: $\lim_{h \to \ 0}\frac{f(x+h)-f(x)}{h}$ $\lim_{h \to \ 0}\frac{f(20+h)-f(20)}{h}$

$\lim_{h \to \ 0} \frac{\tfrac{1}{4}(20 + h)^2 - \tfrac{1}{4}\cdot 20^2}{h} = \lim_{h \to \ 0} \frac{100 + 10h + \tfrac{1}{4}h^2 - 100}{h} = \lim_{h \to \ 0} \frac{h (10 + \tfrac{1}{4}h)}{h} = \lim_{h \to \ 0} (10 + \tfrac{1}{4}h) = 10 \tfrac{m}{s}$ Im letzten Rechenschritt muss Du überlegen, was mit dem Ausdruck $(10 + \tfrac{1}{4}h)$ passiert wenn $h = 0$ ist.

Wenn Du bereits die Potenzregel für Berechnung der Ableitungen kennst, so kannst du die momentane Geschwindigkeit als Wert der Ableitung an dieser Stelle (hier für $t=20$) berechnen:

$f'(20)= \tfrac{1}{4}\cdot2\cdot20 = 10$

Mittelschwere Aufgaben

4. Aufgabe. Überprüfe ob Du alles verstanden hast

Ordne die Begriffe und Abbildungen richtig zu, indem Du sie auf das rechte oder linke Feld ziehst.

Die Begriffe "im Intervall", "zwischen 2 Punkten" oder "Sekante" deuten auf die durchschnittliche Änderungsrate hin. Dagegen deuten "zum Zeitpunkt" oder "Tangente" auf lokale Änderung. Zugehörige Formeln findest du in den Merkkästen.

Aufgabe 5. Bestimme zeichnerisch und rechnerisch die lokale Änderungsrate im vorgegebenen Punkt

Du benötigst für die Aufgabe kariertes Papier, Stifte, Lineal und evtl. einen Taschenrechner.

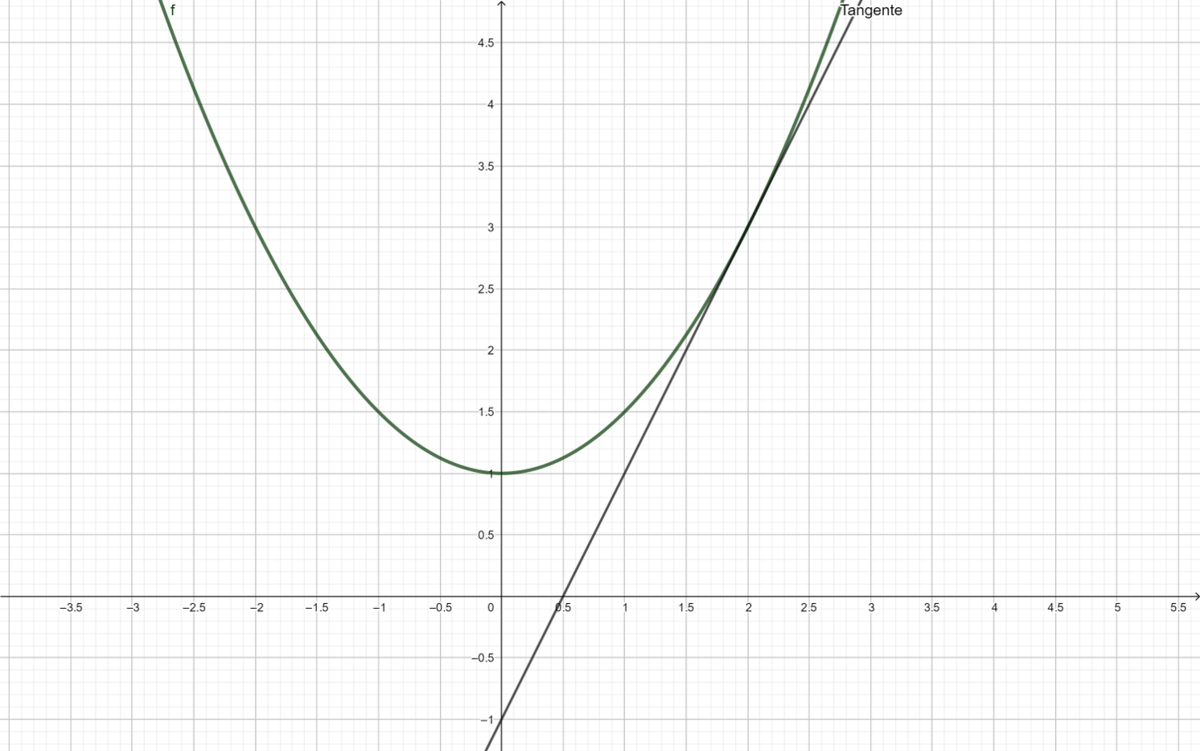
Gegeben sind die Funktionen:

• $f(x)=\tfrac{1}{2}x^2+1$ und der Punkt (2; f(2))

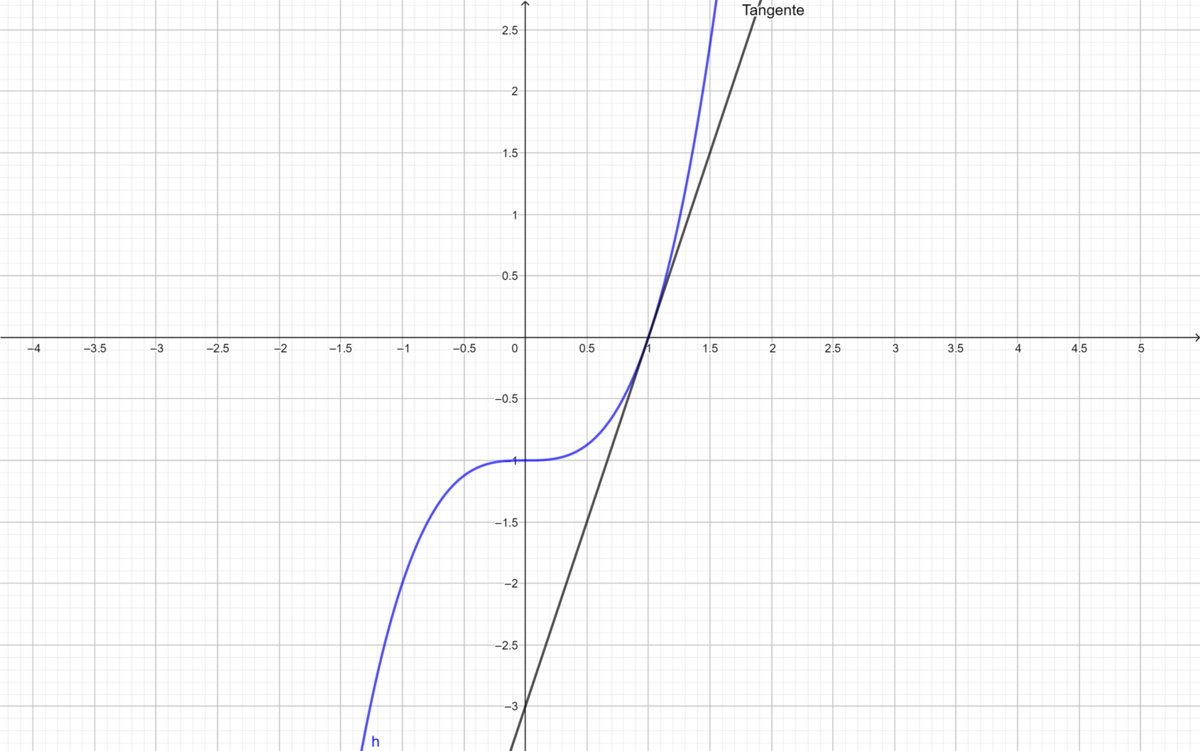
• $h(x)=x^3-1$ und der Punkt (1; h(1))

a) Zeichne die Graphen der Funktionen f(x) und h(x) und skizziere die Tangenten in den angegebenen Punkten.

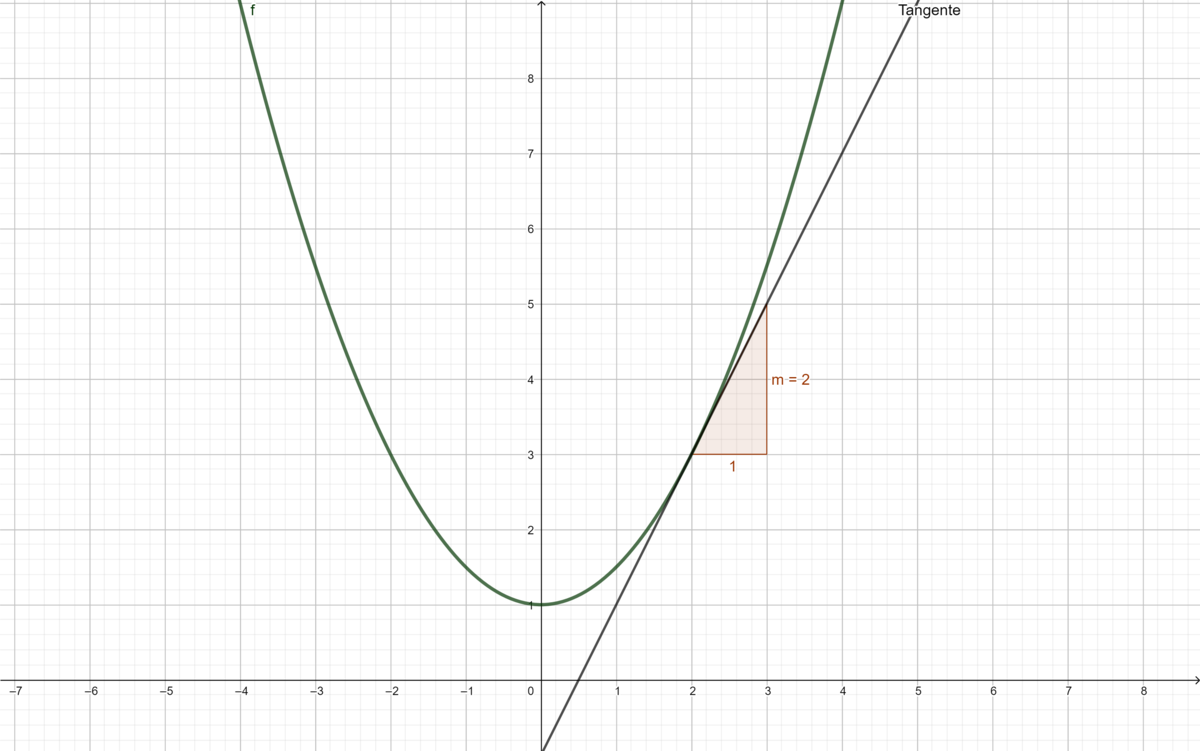
b)Bestimme die Steigung der Funktion im gegebenen Punkt durch Ablesen der Tangentensteigung.

Erinnerst Du dich, dass die Steigung der Funktion in einem Punkt mit der Steigung der Tangente in diesem Punkt übereinstimmt? Für das Ablesen der Tangentensteigung suche Dir am besten ein Intervall zwischen 2 benachbarten ganzen Zahlen, deren Funktionswerte gut abzulesen sind. Steigungsdreieck ist hier das Stichwort.

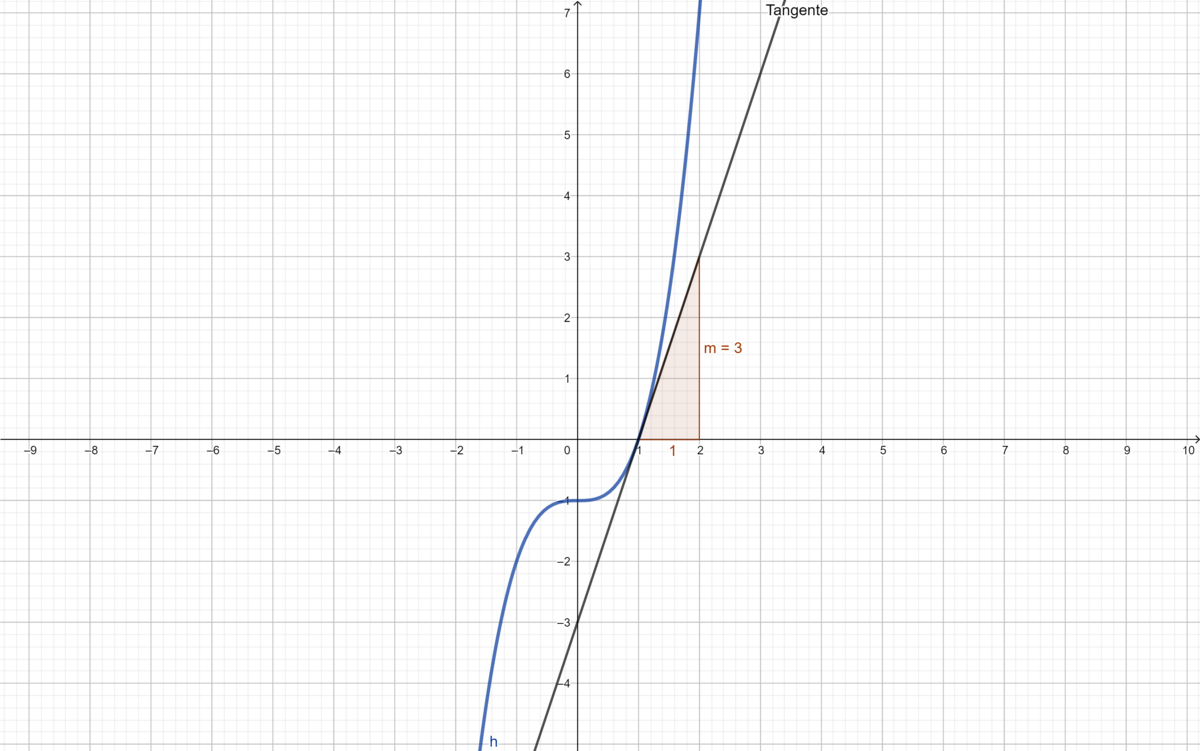
Die Tangente der Funktion $f(x)$ hat an der vorgegebenen Stelle Steigung $m=2$. Die Tangente der Funktion $h(x)$ hat an der Stelle 1 die Steigung $m=3$ Wie komme ich zu meiner Lösung? Beide Steigungen sind am einfachsten im Intervall [1; 2] abzulesen

c) Bestimme rechnerisch die lokale Änderungsrate der jeweiligen Funktion im vorgegebenen Punkt. Vergleiche Deine Ergebnisse mit den Ergebnissen aus Teil b).

Die lokale Änderungsrate im vorgegebenem Punkt berechnest Du am besten mit dieser Formel: $f'(x)=\lim_{h \to \ 0}\frac{f(x+h)-f(x)}{h}$. Hier entspricht die Steigung dem Wert der Ableitung an der vorgegebenen Stelle.

Für die Funktion $f(x)$ rechnest Du also:

$m= \lim_{h \to \ 0}\frac{\tfrac{1}{2}(2+h)^2+1-\tfrac{1}{2}\cdot2^2-1}{h} = \lim_{h \to \ 0}\frac{2 + 2h + 0,5h^2-2}{h}= \lim_{h \to \ 0}(2+0,5h) = 2$ , wenn du $h=0$ einsetzt.

Für die Funktion $h(x)$ rechnest Du:

$m=\lim_{h \to \ 0} \frac{(1+h)^3-1-1^3+1}{h} = \lim_{h \to \ 0} \frac{1+3h+3h^2+h^3-1}{h} = \lim_{h \to \ 0} (3+ 3h + h^2) = 3$

Wenn Du sauber gezeichnet und abgelesen hast, sind die Antworten in den Teilen b) und c) gleich. Die Steigung der Tangente einer Funktion ist also genau die lokale Änderungsrate der Funktion in der kleinsten Umgebung um den Berührungspunkt mit der Tangente.

Aufgabe 6. Anwendung in der Physik

Du benötigst für die Aufgabe Papier, Stifte und einen Taschenrechner.

Nagasaki, 1945 - befor and after

Die Verbreitung der Schockwelle einer atomaren Explosion kann man annähernd mit folgender Funktion beschreiben:

$R(t)=1,6t^2 + 3,2t$

Dabei steht die Variable $t$ für die Zeit nach der Explosion, gemessen in Sekunden, und die Funktion $R(t)$ für den Radius der Verbreitung gemessen in Kilometern.

a) Berechne die mittlere Ausbreitungsgeschwindigkeit $V$ der atomaren Explosion in folgenden Zeitabschnitten:

• ersten drei Sekunden nach der Explosion
• ersten zehn Sekunden nach der Explosion
• im Zeitintervall zwischen der 7. und der 10. Sekunde

Die mittlere Ausbreitungsgeschwindigkeit ist genau die Veränderung (also die Steigung oder die Änderungsrate)der Funktion in einem Zeitabschnitt. Die Steigung der Funktion in einem Intervall wird als Differenzenquotient $\frac{\bigtriangleup R(t)}{\bigtriangleup t}$ berechnet, also hier in diesem Fall als $\frac{Strecke}{Zeit}$

Im Teil a) wird nach dem Differenzenquotient gefragt, den Du mit der Formel : $\frac{f(x_2) - f(x_1)}{x_2-x_1}$ berechnest. Für die ersten 3 Sekunden heißt im Intervall [0; 3],somit: $V= \frac{R(3)-R(0)}{3-0} = \frac{1,6\cdot(3^2) + 3,2\cdot3-0}{3} = \frac{24}{3} = 8$ km/s

Die Lösung für die ersten 10 Sekunden lautet : 19,2 km/s. Im Zeitintervall zwischen der 7. und der 10. Sekunde beträgt die mittlere Ausbreitungsgeschwindigkeit : 30,4 km/s

b) Berechne die Geschwindigkeit der Ausbreitung im angegebenen Zeitpunkt:

• zweite Sekunde nach der Explosion
• zehnte Sekunde nach der Explosion

hier ist nach der momentanen Geschwindigkeit gefragt, geht es also um die durchschnittliche oder lokale Änderungsrate der Funktion? Vergleiche mit dem Teil a). Die entsprechende Berechnungsformeln findest du in Merkkästen am Anfang des Kapitels.

Wird nach der Geschwindigkeit zu einem Zeitpunkt bei einer Weg-Zeit-Funktion gefragt, so handelt es sich um die lokale Änderungsrate, du musst also den Differentialquotienten berechnen. Für die Geschwindigkeit in der zweiten Sekunde rechnest Du also:

$R'(2)=\lim_{h \to \ 0}\frac{R(2+h)-R(2)}{h}$ $=\lim_{h \to \ 0} \frac{1,6 (2+h)^2+3,2\cdot(2+h)-1,6\cdot4-3,2\cdot2}{h} =\lim_{h \to \ 0} (6,4 + 1,6h +3,2) = 8,6$ km/s.

Die momentane Ausbreitungsgeschwindigkeit in der Sekunde 10 beträgt bereits : 35,2 km/s

Aufgabe 7. Änderungsraten im Sachkontext

Überlege zuerst welche Begriffe sind dem x-Wert und dem y-Wert zuzuordnen, was also hängt wie von einander ab. Zum Beispiel hängt die zurückgelegte Strecke von der Fahrzeit ab, damit ist schon mal die Funktion beschrieben. Die Formeln für durchschnittliche und momentane (lokale) Änderungsraten findest du in den Merkkästen.

Knobelaufgaben

Aufgabe 8: Achterbahn

Du benötigst für die Aufgabe kariertes Papier, Stifte, Lineal und evtl. einen Taschenrechner.

Efteling

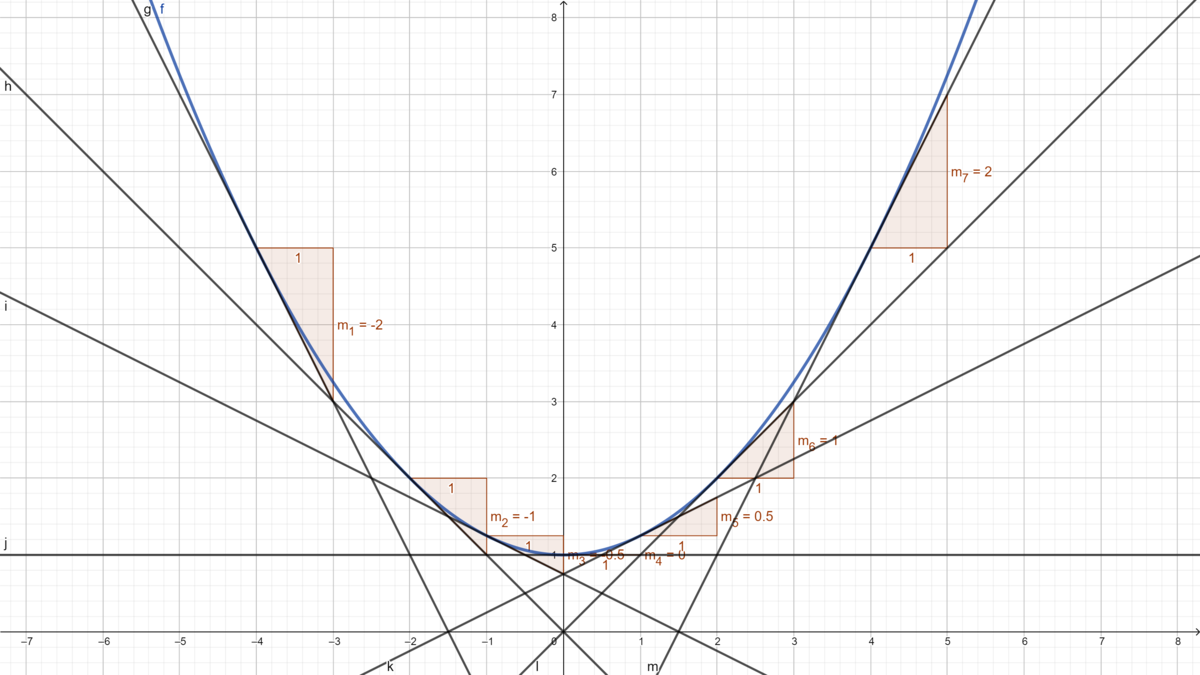
Ein Teil der Achterbahn lässt sich durch den Graphen der Funktion: $f(x) = \tfrac{1}{4}x^2 + 1$ beschreiben.

a)Zeichne den Graphen der Funktion $f(x)$. Vervollständige folgende Tabelle, indem du in den angegebenen Punkten die Tangenten skizzierst und deren Steigungen $m$ durch Ablesen bestimmst.

b) Da es zu jedem Punkt nur eine Tangente gibt, ist die Zuordnung $m \longmapsto x$ eine Funktion $m(x)$. Betrachte die Wertepaare in der Tabelle Teil a). Stelle die Gleichung der Funktion auf und zeichne diese in dein Koordinatensystem.

für alle Wertepaare gilt, dass der Wert $m$ ein Vielfaches von $x$ ist, wobei dieser Faktor eine feste Zahl ist. Solche Zuordnungen nennt man linear.

Die Funktionsgleichung lautet: $m(x) = \tfrac{1}{2} x$. Denn $-1 = 0,5 \cdot (-2) oder 1,5 = 0,5\cdot 3$. Diese Funktion gibt die lokale Steigungsänderung der Achterbahn in Abhängigkeit von dem Streckenpunkt. Dieses Verfahren nennt man graphisches Differenzieren und die Funktion ist die Ableitungsfunktion von $f(x)$. Im Teil c) kannst Du diese Behauptung rechnerisch überprüfen.

c) Berechne den Differentialquotient von $f(x) = \tfrac{1}{4} x^2 + 1$in einem beliebigen Punkt. Vergleiche Dein Ergebnis mit dem Ergebnis von Teil b).

Wir benutzen wie bereits in den Aufgaben davor die h-Formeln für den Differentialquotient. $f'(x) = \lim_{h \to \ 0} \frac{f(x +h) - f(x)}{h} = \lim_{h \to \ 0} \frac{\tfrac{1}{4}(x +h)^2 + 1 - \tfrac{1}{4}x^2-1}{h} = \lim_{h \to \ 0} \frac{\tfrac{1}{4}x^2 +\tfrac{1}{2} xh+\tfrac{1}{4} h^2- \tfrac{1}{4}x^2}{h} = \lim_{h \to \ 0} ( \tfrac{1}{2}x + \tfrac{1}{4}h) = \tfrac{1}{2}x$ Das ist die gleiche Funktion wie beim graphischen Differenzieren im Teil b. Die Ableitung ist also die Steigung der Tangente der Funktion in einem bestimmtem Punkt.

⭐Aufgabe 9.: Tangenten für Funktionenschar

Du benötigst für die Aufgabe Papier, Stifte, Lineal und evtl. einen Taschenrechner.

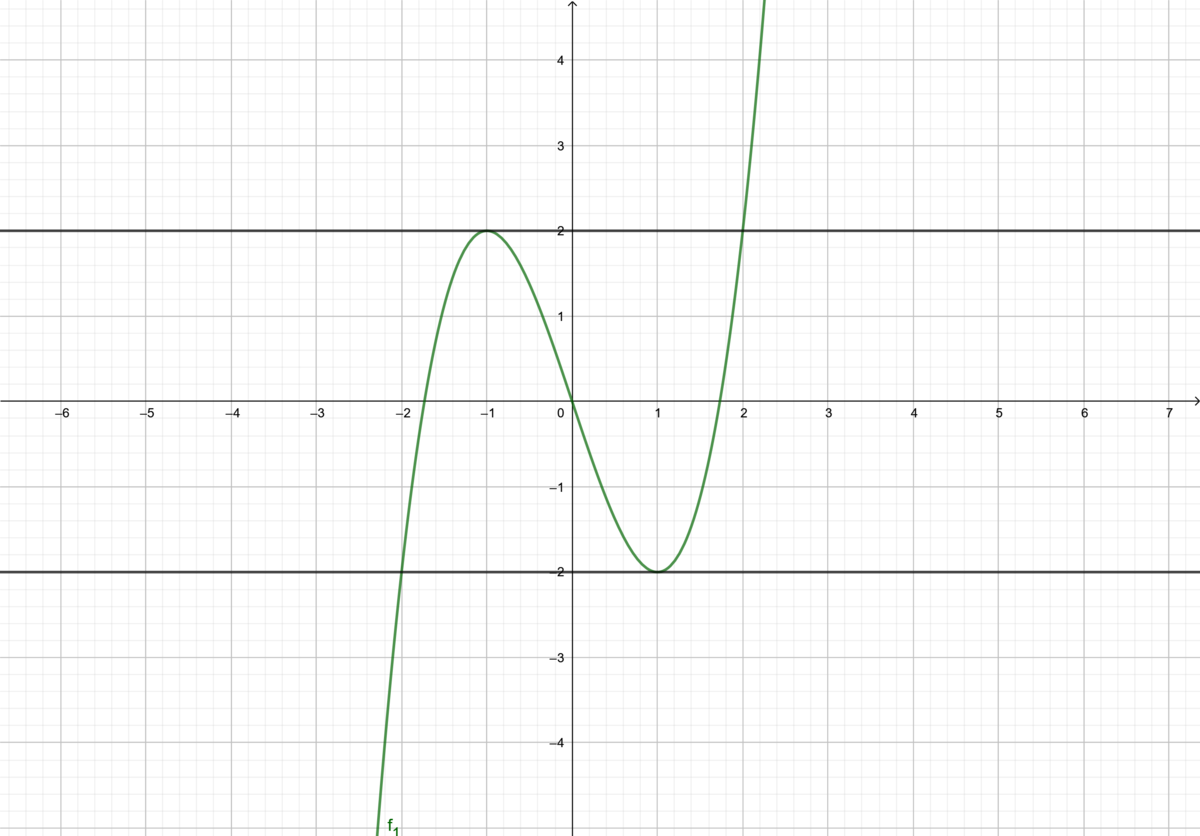
Gegeben ist eine Funktionenschar durch die Gleichung $f_t(x) = x^3 - 3t^2x$ und $t>0$

a) Für welches $t$ ist die 2. Winkelhalbierende $w_2 (x) = -x$ die Tangente im Ursprung?

Die Tangente im Ursprung hat die Formel $T(x) = mx$. Überlege was die Steigung der Tangente $m$ mit der Änderungsrate und der Ableitung zu tun haben. Du suchst eine Tangente mit der Steigung $m=-1$

1)Berechne den Wert der ersten Ableitung der Funktionenshar an der Stelle $x=0$:

$m= f' (0) = -3t^2$.

Also haben die Tangenten durch Ursprung die Formel $T_t(x) = -3t^2x$ mit den Steigungen $m_t = -3t^2$.

2)Wir suchen die Tangente $T_t(x)$ mit Steigung $m=-1$ $- 1 = -3t^2$ $\Leftrightarrow$$t= \sqrt{\tfrac{1}{3}}$

3)Berücksichtige, dass laut der Aufgabe t>0 gilt. Somit ist für $f_\sqrt{\left ( \frac{1}{3} \right )}(x)=x^3-x$ die Tangente im Ursprung die 2. Winkelhalbierende $w_2 (x) = -x$. Diese Funktion ist blau gefärbt.

b) Untersuche, an welchen Stellen die Funktionen der Schar eine waagerechte Tangente haben

Für waagerechte Tangenten gilt : Die Steigung ist 0. Die Steigung der Tangente ist der Wert der Ableitung an dieser Stelle. Du suchst hier also für welche Werte von $x$ in Abhängigkeit von $t$ gilt: $f_t'(x) = 0$ .

$f'(x) = 0$

$\Leftrightarrow$$3x^2 - 3t^2 = 0$

$\Leftrightarrow$$3x^2 = 3t^2$

$\Leftrightarrow$$x = \pm t$ An den Stellen x = t und x = -t haben die Funktionen der Schar eine waagerechte Tangente. Zum Beispiel hat $f_1$ an den Stellen 1 und -1 waagerechte Tangenten.