Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der durchschnittlichen zur lokalen Änderungsrate: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 116: | Zeile 116: | ||
===Mittelschwere Aufgaben=== | ===Mittelschwere Aufgaben=== | ||
{{Box|1=<span style="color: blue">4. Aufgabe. Überprüfe ob Du alles verstanden hast | {{Box|1=<span style="color: blue"></span>4. Aufgabe. Überprüfe ob Du alles verstanden hast|2= | ||
'''''Ordne die Begriffe und Abbildungen richtig zu, indem Du sie auf das rechte oder linke Feld ziehst. '''''{{LearningApp|app=10636537|width=100%|height=600px}} | '''''Ordne die Begriffe und Abbildungen richtig zu, indem Du sie auf das rechte oder linke Feld ziehst. '''''{{LearningApp|app=10636537|width=100%|height=600px}} | ||
| Zeile 123: | Zeile 123: | ||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
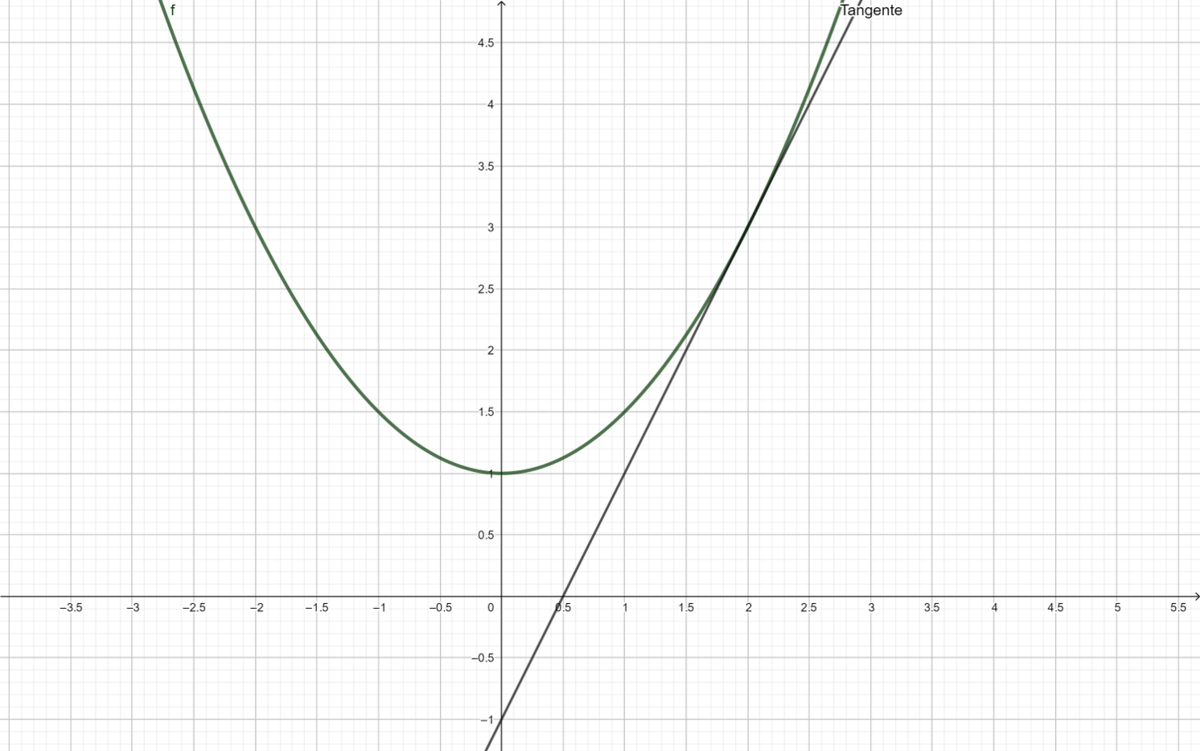
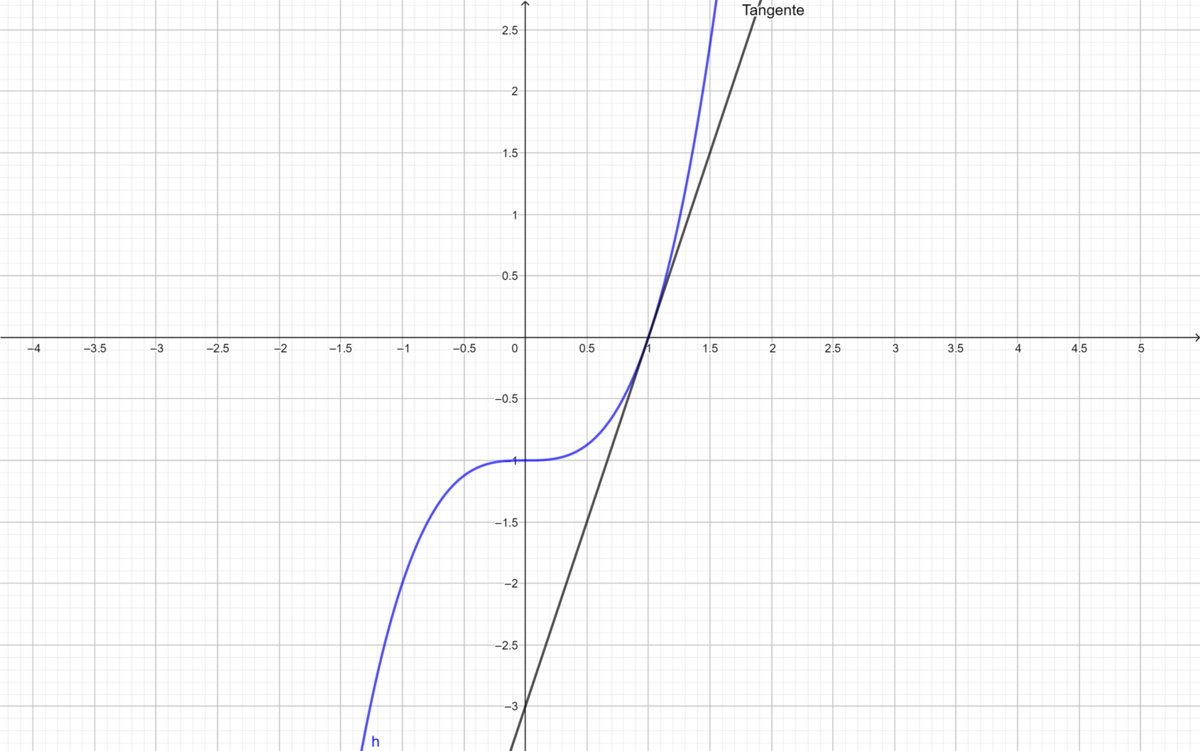
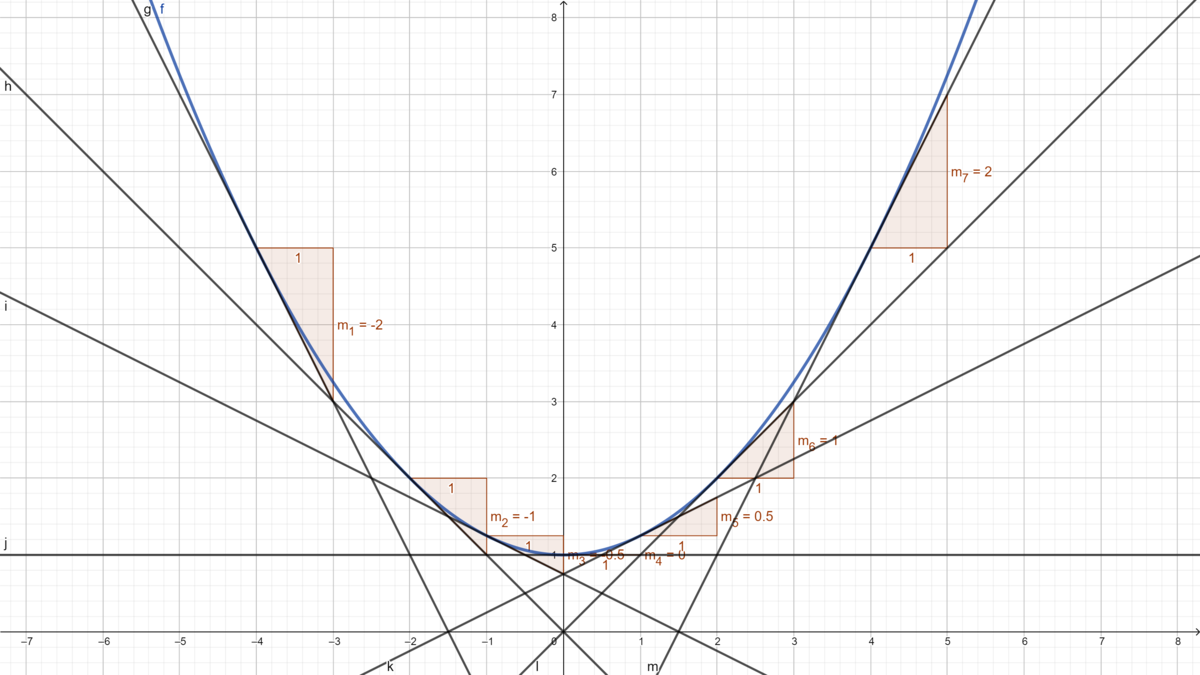
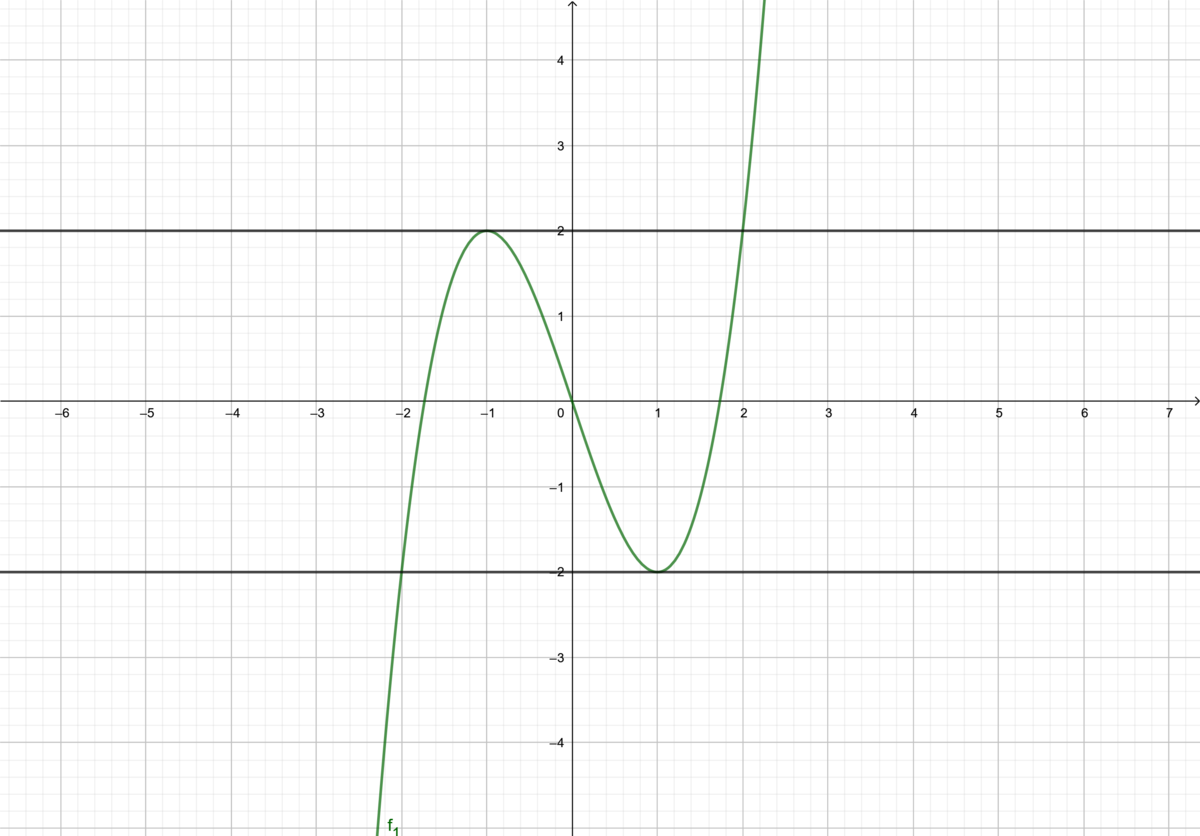
{{Box|1= <span style="color: blue">Aufgabe 5. Bestimme zeichnerisch und rechnerisch die lokale Änderungsrate im vorgegebenen Punkt | {{Box|1= <span style="color: blue"></span>Aufgabe 5. Bestimme zeichnerisch und rechnerisch die lokale Änderungsrate im vorgegebenen Punkt|2= Du benötigst für die Aufgabe kariertes Papier, Stifte, Lineal und evtl. einen Taschenrechner. | ||
Gegeben sind die Funktionen: | Gegeben sind die Funktionen: | ||
| Zeile 161: | Zeile 161: | ||
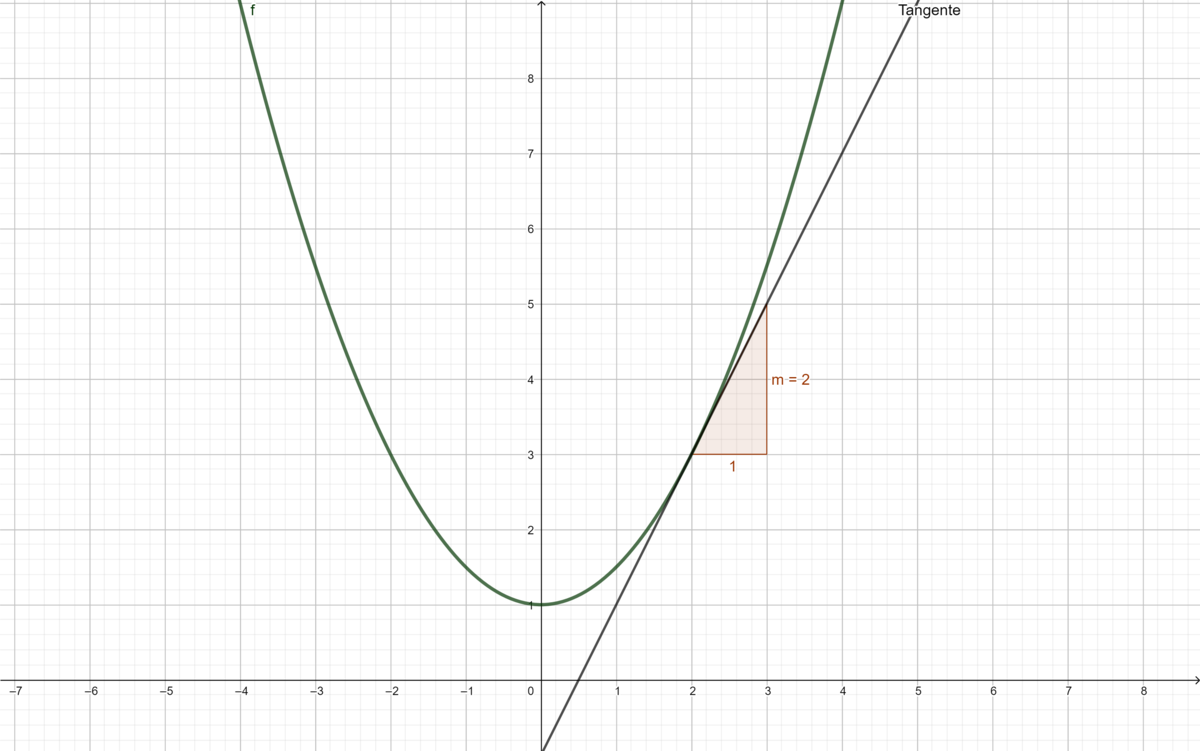
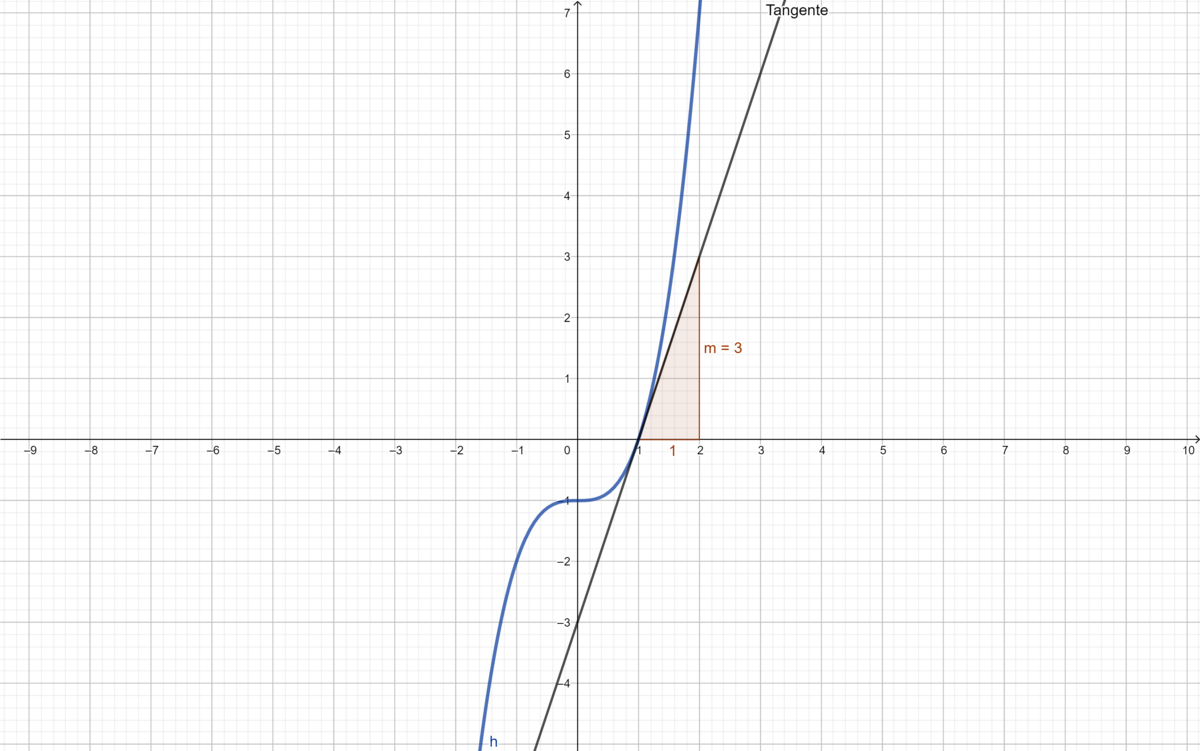
Wenn Du sauber gezeichnet und abgelesen hast, sind die Antworten in den Teilen b) und c) gleich. Die Steigung der Tangente einer Funktion ist also genau die lokale Änderungsrate der Funktion in der kleinsten Umgebung um den Berührungspunkt mit der Tangente. |2=Lösung|3=Lösung}} |3= Arbeitsmethode}} | Wenn Du sauber gezeichnet und abgelesen hast, sind die Antworten in den Teilen b) und c) gleich. Die Steigung der Tangente einer Funktion ist also genau die lokale Änderungsrate der Funktion in der kleinsten Umgebung um den Berührungspunkt mit der Tangente. |2=Lösung|3=Lösung}} |3= Arbeitsmethode}} | ||
{{Box|1= <span style="color: blue">Aufgabe 6. Anwendung in der Physik | {{Box|1= <span style="color: blue"></span>Aufgabe 6. Anwendung in der Physik|2= Du benötigst für die Aufgabe Papier, Stifte und einen Taschenrechner. | ||
[[Datei:Nagasaki 1945 - Before and after (adjusted).jpg|links|thumb|Nagasaki, 1945 - befor and after]] | [[Datei:Nagasaki 1945 - Before and after (adjusted).jpg|links|thumb|Nagasaki, 1945 - befor and after]] | ||
Die Verbreitung der Schockwelle einer atomaren Explosion kann man annähernd mit folgender Funktion beschreiben: | Die Verbreitung der Schockwelle einer atomaren Explosion kann man annähernd mit folgender Funktion beschreiben: | ||
| Zeile 199: | Zeile 199: | ||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
{{Box|1=<span style="color: blue">Aufgabe 7. Änderungsraten im Sachkontext | {{Box|1=<span style="color: blue"></span>Aufgabe 7. Änderungsraten im Sachkontext|2= | ||
{{LearningApp|app=10938377|width=100%|height=600px}} | {{LearningApp|app=10938377|width=100%|height=600px}} | ||
Version vom 19. Mai 2020, 08:06 Uhr
Grundlegende Begriffe und Formeln
Aufgaben zum Wiederholen und Vertiefen
Mittelschwere Aufgaben
Knobelaufgaben