Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der durchschnittlichen zur lokalen Änderungsrate: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 240: | Zeile 240: | ||
''''' | ''''' | ||
{{Lösung versteckt|1 = Die | {{Lösung versteckt|1 = Die Tangente im Ursprung hat die Formel <math>T(x) = mx</math>. Überlege was die Steigung der Tangente <math>m</math> mit der Änderungsrate und der Ableitung zu tun hat. Du suchst eine Tangente mit der Steigung <math>m=-1</math>|2=Tipp|3=Tipp}} | ||
{{Lösung versteckt|1 = | {{Lösung versteckt|1 = 1)Berechne den Wert der ersten Ableitung der Funktionenshar an der Stelle <math>x=0</math>: | ||
<math>m= f' (0) = -3t^2</math>. Also | |||
<math>m= f' (0) = -3t^2</math>. | |||
Also haben die Tangenten durch Ursprung die Formel <math>T_t(x) = -3t^2x</math> mit den Steigungen <math>m_t = -3t^2</math>. | |||
2)Wir suchen die Tangente <math>T_t(x)</math> mit Steigung <math>m=-1</math> | |||
<math>- 1 = -3t^2</math> | |||
<math>\Leftrightarrow</math><math>t= \sqrt{\tfrac{1}{3}}</math> | |||
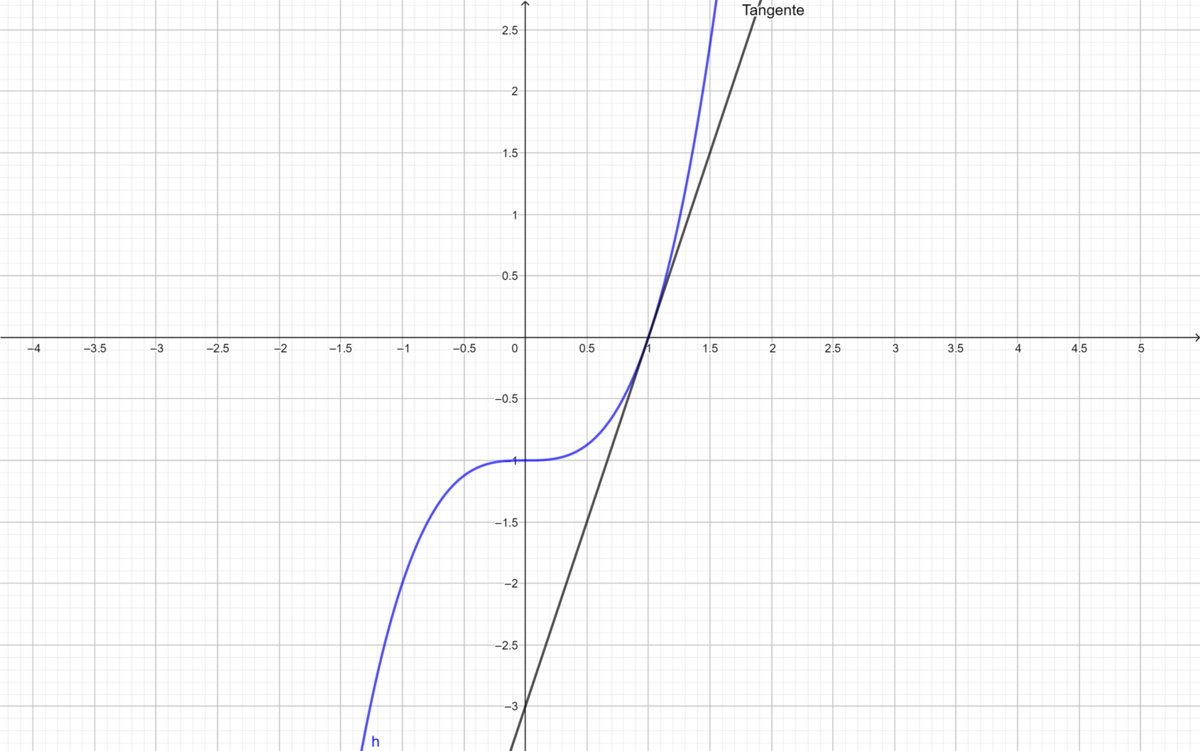
3)Berücksichtige, dass laut der Aufgabe t>0 gilt. Somit ist für <math>f_\sqrt{\left ( \frac{1}{3} \right )}(x)=x^3-x</math> die Tangente im Ursprung die 2. Winkelhalbierende <math>w_2 (x) = -x </math>. Diese Funktion ist blau gefärbt. | |||
[[Datei:Geogebra-exportfunktionenshar.png|1200px|zentriert|rahmenlos]] | |||
|2= Lösung|3=Lösung}} | |2= Lösung|3=Lösung}} | ||
'''''b) Untersuche, an welchen Stellen die Funktionen der Schar eine waagerechte Tangente haben''''' | '''''b) Untersuche, an welchen Stellen die Funktionen der Schar eine waagerechte Tangente haben''''' | ||
{{Lösung versteckt|1 = Für waagerechte Tangenten gilt : Die Steigung ist 0. Die Steigung der Tangente ist der Wert der Ableitung an dieser Stelle. Du suchst hier also für welche Werte von <math> | {{Lösung versteckt|1 = Für waagerechte Tangenten gilt : Die Steigung ist 0. Die Steigung der Tangente ist der Wert der Ableitung an dieser Stelle. Du suchst hier also für welche Werte von <math>x</math> in Abhängigkeit von <math>t</math> gilt: <math>f_t'(x) = 0</math> . | ||
|2= Tipp|3=Tipp}} | |2= Tipp|3=Tipp}} | ||
Version vom 17. Mai 2020, 22:52 Uhr
Grundlegende Begriffe und Formeln
Aufgaben zum Wiederholen und Vertiefen
Mittelschwere Aufgaben
Knobelaufgaben