Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der durchschnittlichen zur lokalen Änderungsrate: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 227: | Zeile 227: | ||
''''' | ''''' | ||
{{Lösung versteckt|1= für alle Wertepaare gilt, dass der Wert <math>m</math> ein Vielfaches von <math>x</math> ist, wobei dieser Faktor eine feste Zahl ist. Solche Zuordnungen nennt man linear.|2=Tipp|3=Tipp}} | {{Lösung versteckt|1= für alle Wertepaare gilt, dass der Wert <math>m</math> ein Vielfaches von <math>x</math> ist, wobei dieser Faktor eine feste Zahl ist. Solche Zuordnungen nennt man linear.|2=Tipp|3=Tipp}} | ||
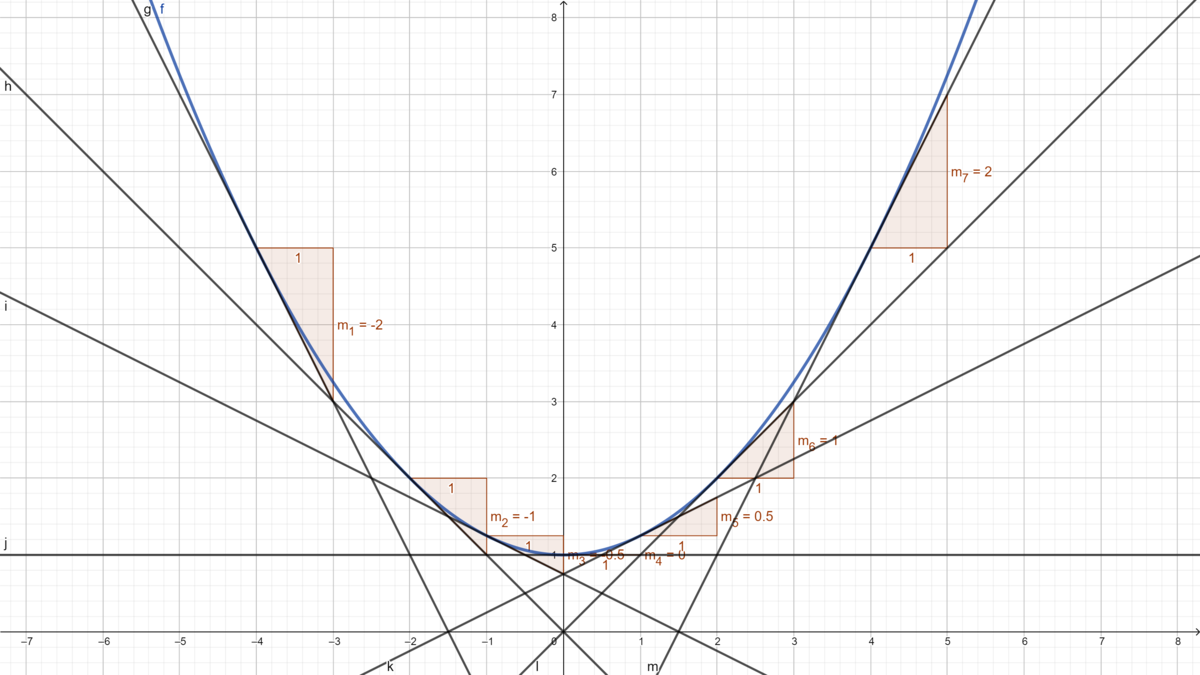
{{Lösung versteckt|1 = Die Funktionsgleichung lautet: <math>m(x) = \tfrac{1}{2} x</math>. Denn <math>-1 = 0,5 \cdot (-2) oder 1,5 = 0,5\cdot 3</math> Diese Funktion gibt die lokale Steigungsänderung | {{Lösung versteckt|1 = Die Funktionsgleichung lautet: <math>m(x) = \tfrac{1}{2} x</math>. Denn <math>-1 = 0,5 \cdot (-2) oder 1,5 = 0,5\cdot 3</math>. Diese Funktion gibt die lokale Steigungsänderung der Achterbahn in Abhängigkeit von dem Streckenpunkt. Dieses Verfahren nennt man graphisches Differenzieren und die Funktion ist die Ableitungsfunktion von f(x). Im Teil c) kannst Du diese Behauptung rechnerisch überprüfen.|2= Lösung|3=Lösung}} | ||
'''''c) Berechne den Differentialquotient von <math>f(x) = \tfrac{1}{4} x^2 + 1 </math>in einem beliebigen Punkt. Vergleiche Dein Ergebnis mit dem Ergebnis von Teil b).''''' | '''''c) Berechne den Differentialquotient von <math>f(x) = \tfrac{1}{4} x^2 + 1 </math>in einem beliebigen Punkt. Vergleiche Dein Ergebnis mit dem Ergebnis von Teil b).''''' | ||
Version vom 17. Mai 2020, 21:48 Uhr
Grundlegende Begriffe und Formeln
Aufgaben zum Wiederholen und Vertiefen
Mittelschwere Aufgaben
Knobelaufgaben