Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Monotonie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Basiswissen Analysis | Eigenschaften von Funktionen und Funktionsuntersuchung
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 48: | Zeile 48: | ||
Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten <math>]-\infty,0[</math> und <math>]0,+\infty[</math>. Darauffolgend berechnen wir die Vorzeichen für die Intervalle. Dies machen wir indem wir Werte für die Ableitung in den entsprechenden Intervallen ausrechnen. Zum Beispiel liegt <math>-2</math> im Intervall <math>]-\infty,0[</math> <math>f'(-2)=-4 <0</math>. Die entsprechenden Werte kannst du in einer Tabelle übersichtlich darstellen: | Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten <math>]-\infty,0[</math> und <math>]0,+\infty[</math>. Darauffolgend berechnen wir die Vorzeichen für die Intervalle. Dies machen wir indem wir Werte für die Ableitung in den entsprechenden Intervallen ausrechnen. Zum Beispiel liegt <math>-2</math> im Intervall <math>]-\infty,0[</math> <math>f'(-2)=-4 <0</math>. Die entsprechenden Werte kannst du in einer Tabelle übersichtlich darstellen: | ||
[[Datei: | [[Datei:Monotonietabelle f(x)=x^2.jpg|links|rahmenlos|900x900px]] | ||
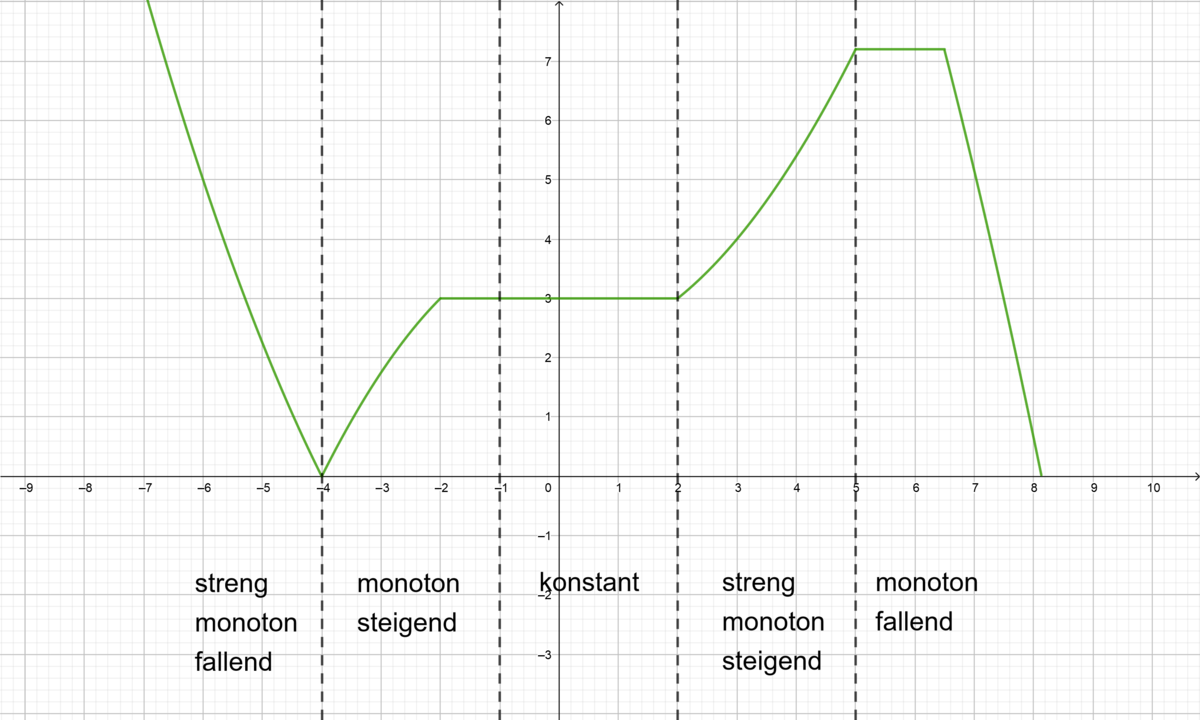
(Legende: <math>\nearrow \widehat{=}</math> streng monoton steigend, <math>\searrow \widehat{=}</math> streng monoton fallend) | (Legende: <math>\nearrow \widehat{=}</math> streng monoton steigend, <math>\searrow \widehat{=}</math> streng monoton fallend) | ||
| Zeile 92: | Zeile 92: | ||
2. Berechne mithilfe deines Taschesrechners die Vorzeichen für die Intervalle | 2. Berechne mithilfe deines Taschesrechners die Vorzeichen für die Intervalle | ||
{{Lösung versteckt|1=[[Datei: | {{Lösung versteckt|1=[[Datei:Tabelle für Aufgabe 2.jpg|links|rahmenlos|900x900px]] |2=Lösung für die Monotonietabelle |3=Schließen}} | ||
Antwort: Somit steigt der Wasserspiegel bis zur Stunde 7,4 (seit Messung). Danach fließt das Wasser ca. bis zur 26. Stunde ab. Anschließend steigt der Wasserspiegel wieder (beispielsweise durch einen erneuten Regenschauer) bis zum Ende des Messzeitraumes. | Antwort: Somit steigt der Wasserspiegel bis zur Stunde 7,4 (seit Messung). Danach fließt das Wasser ca. bis zur 26. Stunde ab. Anschließend steigt der Wasserspiegel wieder (beispielsweise durch einen erneuten Regenschauer) bis zum Ende des Messzeitraumes. | ||
| Zeile 141: | Zeile 141: | ||
2. Berechne mithilfe deines Taschesrechners die Vorzeichen für die Intervalle | 2. Berechne mithilfe deines Taschesrechners die Vorzeichen für die Intervalle | ||
{{Lösung versteckt|1= [[Datei: | {{Lösung versteckt|1= [[Datei:Tabelle Aufgabe 3.jpg|links|rahmenlos|900x900px]] |2=Lösung für die Monotonietabelle |3=Schließen}} | ||
Antwort: Nach Abwurf fällt der Ball zunächst bis er <math>\frac{\sqrt{15}}{5}a</math> cm weit ist. Danch springt wieder hoch bis zum Ende der beobachteten Strecke <math>(x=4)</math>. | Antwort: Nach Abwurf fällt der Ball zunächst bis er <math>\frac{\sqrt{15}}{5}a</math> cm weit ist. Danch springt wieder hoch bis zum Ende der beobachteten Strecke <math>(x=4)</math>. | ||