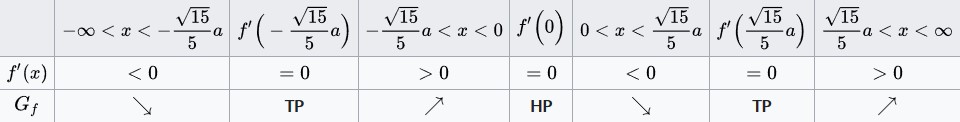Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Monotonie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Basiswissen Analysis | Eigenschaften von Funktionen und Funktionsuntersuchung
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 184: | Zeile 184: | ||
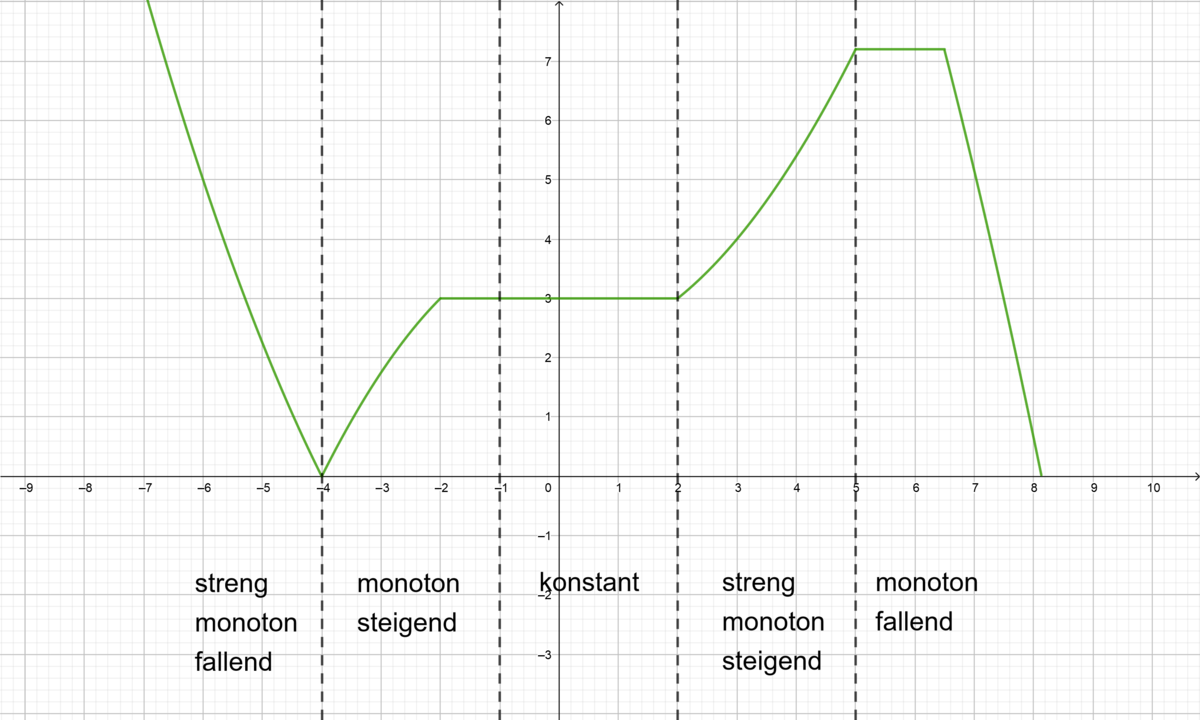
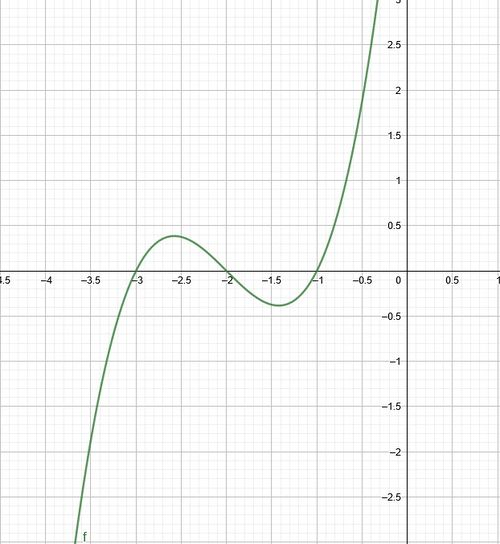
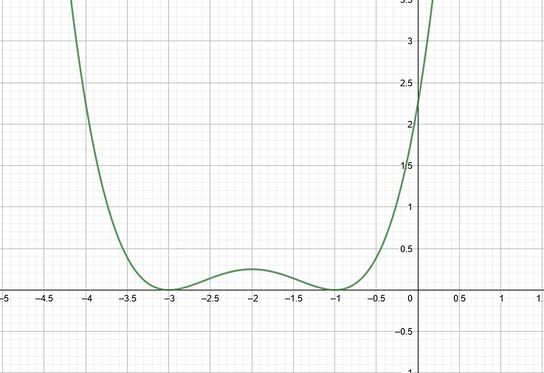
{{Lösung versteckt|1= Die Nullstellen von <math>h'(x)</math> sind <math>x_1=-3, x_2=-2</math> und <math>x_3=-1</math>. | {{Lösung versteckt|1= Die Nullstellen von <math>h'(x)</math> sind <math>x_1=-3, x_2=-2</math> und <math>x_3=-1</math>. | ||
Damit sind die zu betrachtenden Intervalle <math> | Damit sind die zu betrachtenden Intervalle <math>]-\infty, -3[</math>, <math>]-3, -2[</math>, <math>]-2, -1[</math> und <math>]-1, +\infty[</math>. Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob <math>h'(x)</math> an diesen <math><0</math> oder <math>>0</math> ist. | ||
Für <math> | Für <math>]-\infty, -3[</math> ist <math>h'(x)<0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton fallend. | ||
Für <math> | Für <math>]-3, -2[</math> ist <math>h'(x)>0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton steigend. | ||
Für <math> | Für <math>]-2, -1[</math> ist <math>h'(x)<0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton fallend. | ||
Für <math> | Für <math>]-1, +\infty[</math> ist <math>h'(x)>0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton steigend. |2=Lösung|3=Schließen}} | ||