Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Monotonie

Merke

Das Monotonieverhalten einer Funktion beschreibt den Verlauf des Graphen einer Funktion. Die Monotonie gibt an, ob eine Funktion fällt, steigt oder konstant ist.

Sei $f(x)$ eine Funktion und $x_1<x_2$

-      Falls auf einem Intervall $f(x_1) < f(x_2)$ gilt, so ist die Funktion streng monoton steigend

-      Falls auf einem Intervall $f(x_1) \leq \ f(x_2)$ gilt, so ist die Funktion monoton steigend

-      Falls auf einem Intervall $f(x_1) > f(x_2)$ gilt, so ist die Funktion streng monoton fallend

-      Falls auf einem Intervall $f(x_1) \geq \ f(x_2)$ gilt, so ist die Funktion monoton fallend

Wie die einzelnen Eigenschaften am Graphen aussehen, kannst du hier nochmal in der Abbildung sehen!

Aufgabe 1: Zuordnung von Begriffen zur Monotonie

So berechnest du das Monotonieverhalten einer Funktion

1. Erste Ableitung berechnen

2. Nullstellen der ersten Ableitung berechnen

3. Intervalle benennen

4. Monotonietabelle aufstellen

5. Vorzeichen der Intervalle berechnen

6. Ergebnis interpretieren

Beispiel: Monotonieverhalten für $f(x)=x^2$ bestimmen

Zuerst berechnen wir die Ableitung $f'(x)=2x$. Anschließend berechnen wir die Nullstellen der Ableitung ($f'(x)=0$) und erhalten durch Umformungen als Nullstelle $x=0$. Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten $(-\infty,0)$ und $(0,+\infty)$. Darauffolgend stellen wir eine Monotonietabelle auf und berechnen die Vorzeichen für die Intervalle:

Aus dem Ergebnis können wir schließen, dass die Funktion für $(-\infty,0)$ streng monoton fallend und für $(0,+\infty)$ streng monoton steigend ist.

Aufgabe 2: Regenschauer am Aasee

Aasee Münster

Nach einem starken Regenschauer in Münster steigt der Wasserspiegel im Aasee an. Die Funktion $g(x)=\frac{1}{4}x^{3} -\frac{25}{2}x^{2} +144x$ beschreibt die Zuflussgeschwindigkeit in den ersten 48 Stunden ($x=$ Zeit in Stunden, $g(x)\widehat{=}$ Zuflussgeschwindigkeit in Liter pro Stunde). Wann fließt innerhalb dieser Zeit Wasser zu und wann Wasser ab?

Stelle dir vor, wie sich der Graph verändert, wenn Wasser zu- bzw. abfließt

Der Graph steigt monton, wenn Wasser dazufließt und fällt monoton, wenn Wasser abfließt. Also musst du die Monotonie der Funktion $g(x)$ berechnen!

Die Monotonie zeigt uns an, wo der Graph steigt und fällt. In dem Sachzusammenhang somit wann der Wasserspiegel zu und auch abnimmt.

Wir berechnen zuerst die Nullstellen der ersten Ableitung:

$g(x)=\frac{1}{4}x^{3} -\frac{25}{2}x^{2} +144x$

$g'(x)=\frac{3}{4}x^{2} -25x +144$

Durch Umformungen erhalten wir die möglichen Extremstellen:

$\frac{3}{4}x^{2}-25x+144 =0\;\;\;\;\;\;\;\;|:\frac{3}{4}$

$\;x^{2}-\frac{100}{3}x+192 = 0\;\;\;\;\;\;\;\,|$PQ-Formel anwenden

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1/2} = -\frac{p}{2}\pm \sqrt{\Big(\frac{p}{2}\Big)^{2}-q}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= -\frac{-100}{3}\pm \sqrt{\Big(\frac{-100}{3}\Big)^{2}-\Big(192\Big)}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Rightarrow x_{1} = 25,92$ und $x_{2} = 7,40$

Mithilfe der errechneten Intervalle können wir nun die Monotonietabelle aufstellen:

Antwort: Somit fließt Wasser steigt der Wasserspiegel bis zur Stunde 7,4 (seit Messung). Danach fließt es ca. bis zur 26. Stunde ab.

Aufgabe 3: Der"SuperBounce"-Ball ⭐

SuperBounce-Ball

Die Firma "SuperBounce" hat einen speziellen Ball erfunden, der eine einzigartige Sprungbewegung beim Wurf auf dem Boden erzeugt. Die Funktion $f_a(x)=\frac{5}{6}x^{4}-a^{2}x^{2}$ beschreibt annähernd die Flugbahn des Balles, wobei $a\in[-3,3]$ die Härte des Wurfes durch den Werfer beschreibt ($x=$horizontaler Verlauf des Balles in cm, $f_a(x)\widehat{=}$Höhe des Balles in cm). Bestimme wann der Ball in Abhängikeit von $a$ nach oben springt und wann er fällt.

Überlege, wie sich das sprunghafte Verhalten des Balles im Graphen erkennen lässt.

Um zu berechnen, wann der Ball springt und wann er fällt, berechnen wir das Monotonieverhalten der Funktion.

Wir berechnen zuerst die Nullstellen der ersten Ableitung:

$f_a(x)=\frac{5}{6}x^{4}-a^{2}x^{2}$

$f_a'(x)=\frac{20}{6}x^{3}-2a^{2}x$

Durch Umformungen erhalten wir die möglichen Extremstellen:

$\;\;\;\;\;\;\frac{20}{6}x^{3}-2a^{2}x =0\;\;\;\;\;\;\;|$ Ausklammern

$\;x\cdot(\frac{20}{6}x^{2}-2a^{2})=0\;\;\;\;\;\;\;|$ Satz vom Nullprodukt

$\Rightarrow x_{1} = 0$

$oder\;\;\;\;\;\;\ \frac{20}{6}x^{2} - 2a^{2} = 0\;\;\;\;\;\;\,\;|+2a^{2}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \frac{20}{6}x^{2}= 2a^{2}\;\;\;\;|:\frac{20}{6}$

$\;\;\;\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x^{2} = \frac{3}{5}a^{2}\;|\sqrt{(...)}$

.$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Rightarrow x_{1} = 0, x_{2} = \frac{\sqrt{15}}{5}a,$ und $x_{3} =-\frac{\sqrt{15}}{5}a$

Mithilfe der errechneten Intervalle können wir nun die Monotonietabelle aufstellen:

Aufgabe 4: Monotonieverhalten anhand der Ableitungsfunktion bestimmen

a) Auf dem Bild siehst du den Graphen einer Ableitungsfunktion $h'(x)$. Welche Aussagen kannst du über das Monotonieverhalten von $h(x)$ machen?

Erinnere dich daran, wie du bei der Berechnung des Monotonieverhaltens vorgehst. Welche Aussagen zum Monotonieverhalten liefert dir $h'(x)=0$?

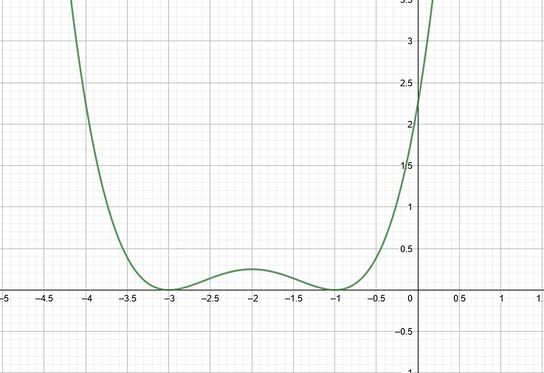
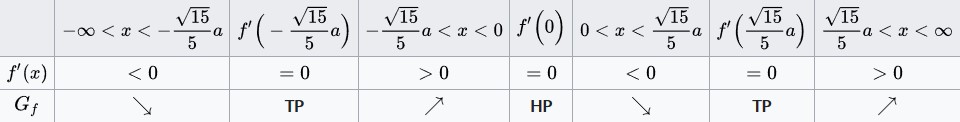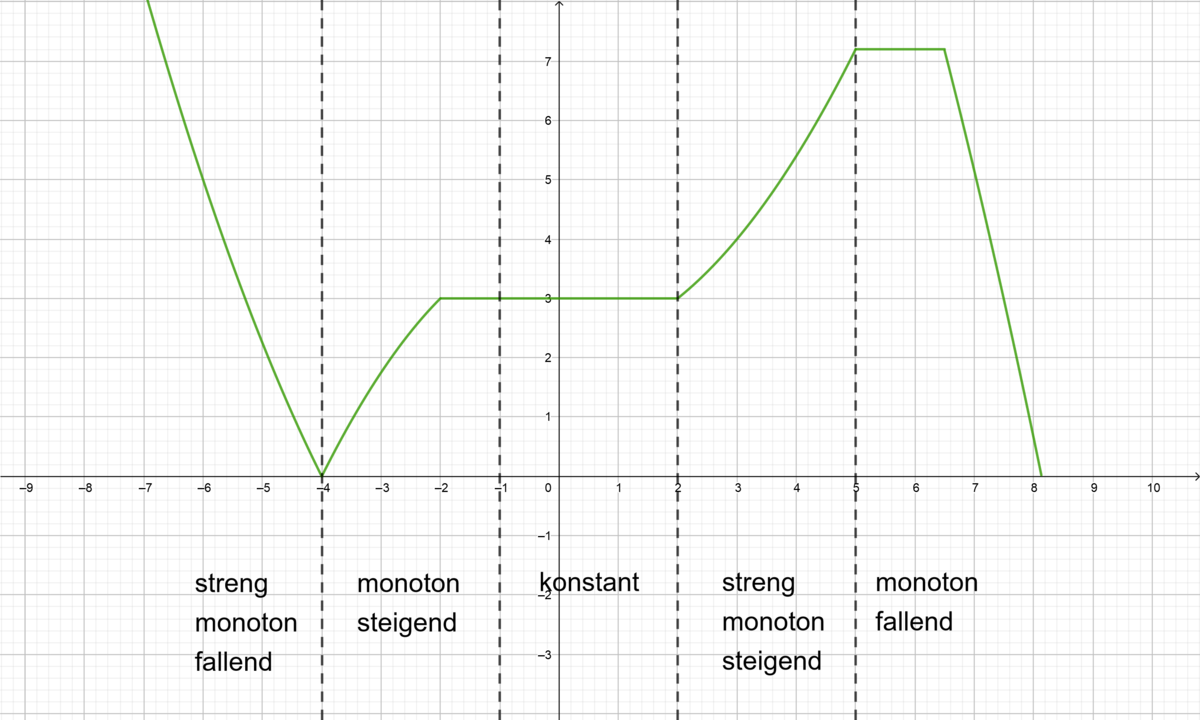
Die Nullstellen von $h'(x)$ definieren die verschiedenen Intervalle, in denen das Monotonieverhalten von $h$ verschieden ist. Nun kannst du betrachten, auf welchen Intervallen $h'(x)$ $<0$ bzw. $>0$ ist. Welche Aussagen kannst du damit über das Monotonieverhalten von $h(x)$ machen?

Die Nullstellen von $h'(x)$ sind $x_1=-3, x_2=-2$ und $x_3=-1$.

Damit sind die zu betrachtenden Intervalle $(-\infty, -3)$, $(-3, -2)$, $(-2, -1)$ und $(-1, +\infty)$. Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob $h'(x)$ an diesen $<0$ oder $>0$ ist.

Für $(-\infty, -3)$ ist $h'(x)<0$, somit ist $h(x)$ auf diesem Intervall streng monoton fallend.

Für $(-3, -2)$ ist $h'(x)>0$, somit ist $h(x)$ auf diesem Intervall streng monoton steigend.

Für $(-2, -1)$ ist $h'(x)<0$, somit ist $h(x)$ auf diesem Intervall streng monoton fallend.

Für $(-1, +\infty)$ ist $h'(x)>0$, somit ist $h(x)$ auf diesem Intervall streng monoton steigend.

b) Zeichne nun mithilfe deiner Ergebnisse aus a) den Funktionsgraphen $h(x)$ mithilfe deiner Kenntnisse über sein Monotonieverhalten in dein Heft.

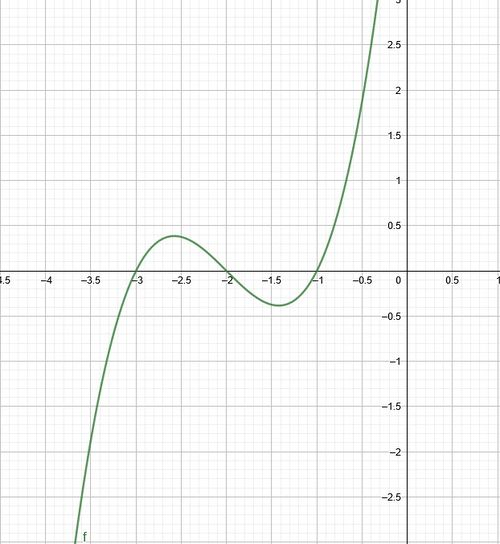
Dein Graph könnte in etwa so aussehen:

Möglich, weitere Lösungen für die Zeichnung des Graphen sind unter anderem Verschiebungen in Richtung der Ordinate, also nach unten und oben oder auch Streckungen bzw. Stauchungen.

zurück

Extrema