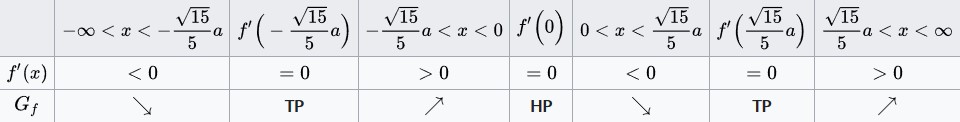Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Monotonie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Basiswissen Analysis | Eigenschaften von Funktionen und Funktionsuntersuchung
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 54: | Zeile 54: | ||
{{Box | Aufgabe 2 | | {{Box | Aufgabe 2: Regenschauer am Aasee | | ||
Nach einem starken Regenschauer in Münster steigt der Wasserspiegel im Aasee an. Die Funktion <math>f(x)=\frac{1}{4}x^{3} -\frac{25}{2}x^{2} +144x</math> beschreibt die Zuflussgeschwindigkeit in den ersten 48 Stunden (<math>x=</math> Zeit in Stunden, <math>f(x)=</math> Zuflussgeschwindigkeit in Liter pro Stunde). Wann fließt innerhalb dieser Zeit Wasser zu und wann Wasser ab? | Nach einem starken Regenschauer in Münster steigt der Wasserspiegel im Aasee an. Die Funktion <math>f(x)=\frac{1}{4}x^{3} -\frac{25}{2}x^{2} +144x</math> beschreibt die Zuflussgeschwindigkeit in den ersten 48 Stunden (<math>x=</math> Zeit in Stunden, <math>f(x)=</math> Zuflussgeschwindigkeit in Liter pro Stunde). Wann fließt innerhalb dieser Zeit Wasser zu und wann Wasser ab? | ||
| Zeile 90: | Zeile 89: | ||
|2=Lösung|3=Schließen}} | |2=Lösung|3=Schließen}} | ||
| Farbe= #0000CD| Arbeitsmethode}} | |||
{{Box | Aufgabe 3: Der"SuperBounce Ball" ⭐ | ⭐ | |||
Die Firma "SuperBounce" hat einen speziellen Ball erfunden, der eine einzigartige Sprungbewegung beim Wurf auf dem Boden erzeugt. Die Funktion <math>f(x)=\frac{5}{6}x^{4}-a^{2}x^{2}</math> beschreibt annähernd die Flugbahn des Balles, wobei <math>a\in[-3,3]</math> die Härte des Wurfes durch den Werfer beschreibt (<math>x=</math>horizontaler Verlauf des Balles in cm, <math>f(x)=</math>Höhe des Balles in cm). Bestimme wann der Ball in Abhängikeit von <math>a</math> nach oben springt und wann er fällt. | Die Firma "SuperBounce" hat einen speziellen Ball erfunden, der eine einzigartige Sprungbewegung beim Wurf auf dem Boden erzeugt. Die Funktion <math>f(x)=\frac{5}{6}x^{4}-a^{2}x^{2}</math> beschreibt annähernd die Flugbahn des Balles, wobei <math>a\in[-3,3]</math> die Härte des Wurfes durch den Werfer beschreibt (<math>x=</math>horizontaler Verlauf des Balles in cm, <math>f(x)=</math>Höhe des Balles in cm). Bestimme wann der Ball in Abhängikeit von <math>a</math> nach oben springt und wann er fällt. | ||
| Zeile 131: | Zeile 131: | ||
|2=Lösung|3=Schließen}} | |2=Lösung|3=Schließen}} | Farbe= #0000CD| Arbeitsmethode}} | ||
{{Box | Aufgabe | {{Box | Aufgabe 4: Monotonieverhalten anhand der Ableitungsfunktion bestimmen | | ||
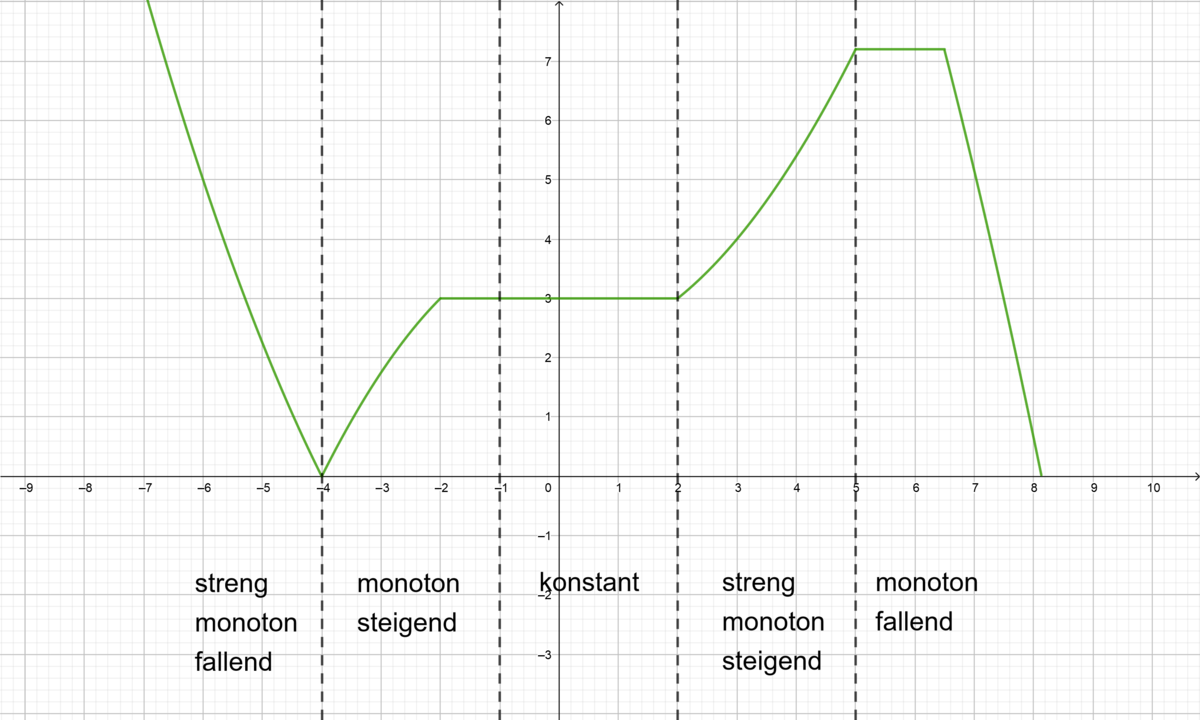
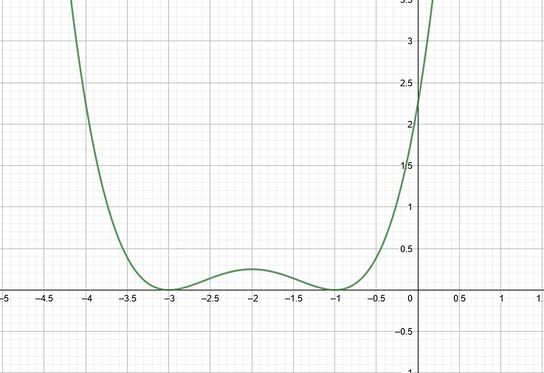
'''a)''' Auf dem Bild siehst du den Graphen einer Ableitungsfunktion <math> | '''a)''' Auf dem Bild siehst du den Graphen einer Ableitungsfunktion <math>h'(x)</math>. Welche Aussagen kannst du über das Monotonieverhalten von <math>h(x)</math> machen? | ||
| Zeile 172: | Zeile 171: | ||
{{Lösung versteckt|1=Erinnere dich daran, wie du bei der Berechnung des Monotonieverhaltens vorgehst. Welche Aussagen zum Monotonieverhalten liefert dir <math> | {{Lösung versteckt|1=Erinnere dich daran, wie du bei der Berechnung des Monotonieverhaltens vorgehst. Welche Aussagen zum Monotonieverhalten liefert dir <math>h'(x)=0</math>? |2=Tipp 1|3=Schließen}} | ||
{{Lösung versteckt|1=Die Nullstellen von <math> | {{Lösung versteckt|1=Die Nullstellen von <math>h'(x)</math> definieren die verschiedenen Intervalle, in denen das Monotonieverhalten von <math>h</math> verschieden ist. Nun kannst du betrachten, auf welchen Intervallen <math>h'(x)</math> <math><0</math> bzw. <math>>0</math> ist. Welche Aussagen kannst du damit über das Monotonieverhalten von <math>h(x)</math> machen? |2=Tipp 2|3=Schließen}} | ||
{{Lösung versteckt|1= Die Nullstellen von <math> | {{Lösung versteckt|1= Die Nullstellen von <math>h'(x)</math> sind <math>x_1=-3, x_2=-2</math> und <math>x_3=-1</math>. | ||
Damit sind die zu betrachtenden Intervalle <math>(-\infty, -3)</math>, <math>(-3, -2)</math>, <math>(-2, -1)</math> und <math>(-1, +\infty)</math>. Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob <math> | Damit sind die zu betrachtenden Intervalle <math>(-\infty, -3)</math>, <math>(-3, -2)</math>, <math>(-2, -1)</math> und <math>(-1, +\infty)</math>. Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob <math>h'(x)</math> an diesen <math><0</math> oder <math>>0</math> ist. | ||
Für <math>(-\infty, -3)</math> ist <math> | Für <math>(-\infty, -3)</math> ist <math>h'(x)<0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton fallend. | ||
Für <math>(-3, -2)</math> ist <math> | Für <math>(-3, -2)</math> ist <math>h'(x)>0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton steigend. | ||
Für <math>(-2, -1)</math> ist <math> | Für <math>(-2, -1)</math> ist <math>h'(x)<0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton fallend. | ||
Für <math>(-1, +\infty)</math> ist <math> | Für <math>(-1, +\infty)</math> ist <math>h'(x)>0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton steigend. |2=Lösung|3=Schließen}} | ||
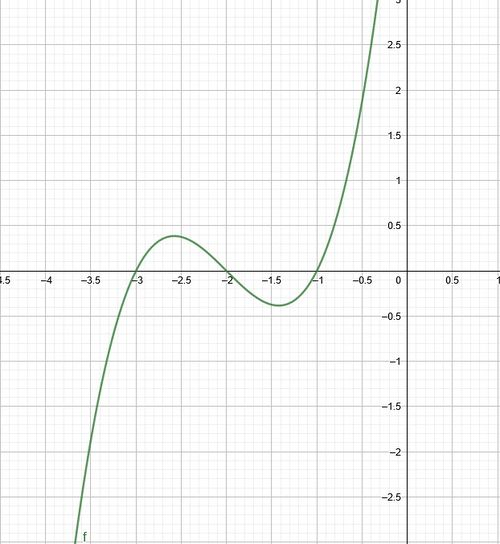
'''b)''' Zeichne nun mithilfe deiner Ergebnisse aus a) den Funktionsgraphen <math> | '''b)''' Zeichne nun mithilfe deiner Ergebnisse aus a) den Funktionsgraphen <math>h(x)</math> mithilfe deiner Kenntnisse über sein Monotonieverhalten in dein Heft. | ||
{{Lösung versteckt|1=Dein Graph könnte in etwa so aussehen: | {{Lösung versteckt|1=Dein Graph könnte in etwa so aussehen: | ||