Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Wendepunkte: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Basiswissen Analysis | Eigenschaften von Funktionen und Funktionsuntersuchung
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
{{Box | Merke: | {{Box | Merke: Änderung des Krümmungsverhalten| | ||
'''Ein Wendepunkt''' beschreibt einen Punkt auf einem Funktionsgraphen an dem sich das '''Krümmungsverhalten des | '''Ein Wendepunkt''' beschreibt einen Punkt auf einem Funktionsgraphen, an dem sich das '''Krümmungsverhalten des Graphen ändert'''. Der Funktionsgraph ändert an dieser Stelle seine Krümmung von rechts nach links (Rechts-Links-Wendestelle, kurz: RLW) oder von links nach rechts (Links-Rechts-Wendestelle, kurz: LRW). | ||
Tipp: Es kann helfen, wenn man sich vorstellt auf dem Graphen mit einem Fahrrad zu fahren, so ist der Wendepunkt genau an dem Punkt, wo sich die Richtung, in die man lenkt, ändert. | Tipp: Es kann helfen, wenn man sich vorstellt auf dem Graphen mit einem Fahrrad zu fahren, so ist der Wendepunkt genau an dem Punkt, wo sich die Richtung, in die man lenkt, ändert. | ||
| Zeile 9: | Zeile 9: | ||
{{Box |1= Aufgabe 1 - Wendepunkte angeben | {{Box |1= Aufgabe 1 - Wendepunkte angeben | ||
|2= | |2= | ||
{{LearningApp|width:80%|height:450px|app=pasf50isa20}}|3=Arbeitsmethode| Farbe={{Farbe|orange}}}} | {{LearningApp|width:80%|height:450px|app=pasf50isa20}}|3=Arbeitsmethode| Farbe={{Farbe|orange}}}} | ||
{{Box | Merke: | {{Box | Merke: Lokales Extremum der Ableitung | ||
|An einem '''Wendepunkt''' <math> x_W </math> einer Funktion <math>f(x)</math> ist die '''Steigung''' in der näheren Umgebung '''maximal bzw. minimal'''. Somit folgt, dass die Ableitung an dieser Stelle ein lokales Extremum aufweist. Daraus ergibt sich das notwendige Kriterium für einen Wendepunkt. | |An einem '''Wendepunkt''' <math> x_W </math> einer Funktion <math>f(x)</math> ist die '''Steigung''' in der näheren Umgebung '''maximal bzw. minimal'''. Somit folgt, dass die Ableitung an dieser Stelle ein lokales Extremum aufweist. Daraus ergibt sich das notwendige Kriterium für einen Wendepunkt. Wenn die Funktion <math>f'(x)</math> im Punkt <math> x_W </math> einen Extrempunkt aufweist, so ist die Ableitung dieser Funktion <math>f''(x)</math> in diesem Punkt gleich 0 (Hinweis: Dies wurde im vorherigen Kapitel "Extema" bearbeitet). | ||
'''Zusammenfassung:''' | '''Zusammenfassung:''' | ||
| Zeile 22: | Zeile 22: | ||
{{Box| | {{Box|Berechnung eines Wendepunktes| | ||
* '''Notwendiges Kriterium:''' Nullstellen <math> x_W </math> der zweiten Ableitung berechnen | * '''Notwendiges Kriterium:''' Nullstellen <math> x_W </math> der zweiten Ableitung berechnen | ||
| Zeile 60: | Zeile 60: | ||
<math>f(x_{W_{2}})=\frac{7}{12}\cdot (-20)^4-5\cdot (-20)^2-90.000=\frac{4.000}{3}\approx 1.333,33</math> | <math>f(x_{W_{2}})=\frac{7}{12}\cdot (-20)^4-5\cdot (-20)^2-90.000=\frac{4.000}{3}\approx 1.333,33</math> | ||
'''Lösung:''' An dem Punkt <math>(20 | '''Lösung:''' An dem Punkt <math>(20|\frac{4.000}{3})</math> liegt eine Recht-links-Wendepunkt vor und an dem Punkt <math>(-20|\frac{4.000}{3})</math> liegt ein Links-rechts-Wendepunkt vor. | ||
| Beispiel anzeigen |Beispiel verbergen}} | | Beispiel anzeigen |Beispiel verbergen}} | ||
| Wie berechnet man einen Wendepunkt}} | | Wie berechnet man einen Wendepunkt}} | ||
{{Box|1= Aufgabe 2 - Wendepunkt bestimmen | {{Box|1= Aufgabe 2 - Wendepunkt bestimmen | ||
|2=Berechne die Wendepunkte der folgenden Funktionen. Falls du Hilfe brauchst, schaue dir zunächst die Tipps an. | |2=Berechne die Wendepunkte der folgenden Funktionen. Falls du Hilfe brauchst, schaue dir zunächst die Tipps an. Der Aufgabenteil b) geht über Funktionsscharen und ist nur für den LK gedacht. | ||
'''a)''' <math> g(x) = \frac{2}{25} x^5-x^3+\frac{25}{8} x </math> | '''a)''' <math> g(x) = \frac{2}{25} x^5-x^3+\frac{25}{8} x </math> | ||
{{Lösung versteckt|Schaue dir das obige Beispiel nochmal genau an!| Tipp 1 |Tipp verbergen}} | {{Lösung versteckt|Schaue dir das obige Beispiel nochmal genau an!| Tipp 1 |Tipp verbergen}} | ||
{{Lösung versteckt|Versuche die drei Ableitungen von der Funktion zu berechnen und schaue dir dann die Kriterien für einen Wendepunkt an!| Tipp 2 |Tipp verbergen}} | {{Lösung versteckt|Versuche, die drei Ableitungen von der Funktion zu berechnen und schaue dir dann die Kriterien für einen Wendepunkt an!| Tipp 2 |Tipp verbergen}} | ||
{{Lösung versteckt|Um die Nullstelle eine Polynoms dritten Grades zu berechnen, | {{Lösung versteckt|Um die Nullstelle eine Polynoms dritten Grades zu berechnen, kannst du ein <math>x</math> ausklammern.| Tipp 3| Tipp verbergen}} | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
Schaue dir hier die Rechnung an um den Lösungsweg schrittweise nachzuvollziehen! | Schaue dir hier die Rechnung an um den Lösungsweg schrittweise nachzuvollziehen! | ||
| Zeile 123: | Zeile 122: | ||
| Rechenweg anzeigen |Rechenweg verbergen}} | | Rechenweg anzeigen |Rechenweg verbergen}} | ||
'''Lösung:''' An dem Punkt <math>(0/0)</math> liegt eine Links-rechts-Wendepunkt vor und an den Punkten <math>(\sqrt{\frac{30}{8}} | '''Lösung:''' An dem Punkt <math>(0/0)</math> liegt eine Links-rechts-Wendepunkt vor und an den Punkten <math>(\sqrt{\frac{30}{8}}|0,97)</math> und <math>(-\sqrt{\frac{30}{8}}|-0,97)</math> liegen Rechts-links-Wendepunkte vor. | ||
| Lösung anzeigen |Lösung verbergen}} | | Lösung anzeigen |Lösung verbergen}} | ||
| Zeile 176: | Zeile 175: | ||
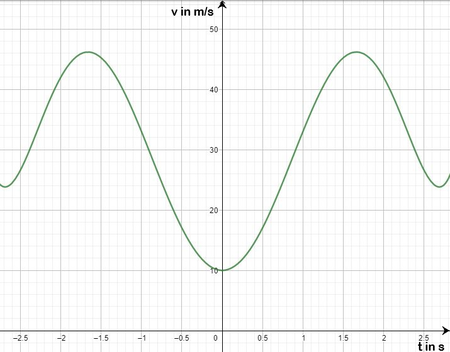
An den Stellen, wo die Achterbahn stark abbremst oder beschleunigt sind die wichtigsten Stellen der Fahrt. Zu diesen Zeitpunkten sollen deshalb besondere Sicherheitssysteme arbeiten. Berechne mit Hilfe der Funktion <math> v(t) </math> | An den Stellen, wo die Achterbahn stark abbremst oder beschleunigt, sind die wichtigsten Stellen der Fahrt. Zu diesen Zeitpunkten sollen deshalb besondere Sicherheitssysteme arbeiten. Berechne mit Hilfe der Funktion <math> v(t) </math>, zu welchen Zeitpunkten die Beschleunigung minimal bzw. maximal ist. '''Beachte:''' Es ist nur der '''Zeitpunkt''' du musst also nicht den Funktionswert bzw. die Geschwindigkeit berechnen, der letzte Schritt in unserem Beispiel bleibt also aus. | ||
{{Lösung versteckt|Die Beschleunigung <math>a(t)</math> kann man | {{Lösung versteckt|Die Beschleunigung <math>a(t)</math> kann man ermitteln, da sie der Ableitung der Geschwindigkeit entspricht also: <math>a(t)=v'(t)</math>. Die Geschwindigkeit ist angegeben. Was gilt für die Punkte, wo die Beschleunigung maximal oder minimal ist? Lösung zu der Frage findest du in Tipp 2.| Tipp 1 anzeigen |Tipp verbergen}} | ||
{{Lösung versteckt|Zu dem Zeitpunkt <math>t_{W}</math> an dem die Beschleunigung maximal bzw. minimal ist gilt: <math>a'(t_{W})=0</math>, da zu diesem Zeitpunkt die Beschleunigung eine Extremstelle und somit die Geschwindigkeit einen Wendepunkt aufweist. | {{Lösung versteckt|Zu dem Zeitpunkt <math>t_{W}</math> an dem die Beschleunigung maximal bzw. minimal ist gilt: <math>a'(t_{W})=0</math>, da zu diesem Zeitpunkt die Beschleunigung eine Extremstelle und somit die Geschwindigkeit einen Wendepunkt aufweist. | ||
Hier muss also nur wieder der Wendepunkt berechnet werden. Falls du noch mehr Hilfe brauchst, schau dir die Tipps von Aufgabe 2 und das Beispiel nochmal an!| Tipp 2 anzeigen |Tipp verbergen}} | Hier muss also nur wieder der Wendepunkt berechnet werden. Falls du noch mehr Hilfe brauchst, schau dir die Tipps von Aufgabe 2 und das Beispiel nochmal an!| Tipp 2 anzeigen |Tipp verbergen}} | ||