Benutzer:Lena H. WWU-5/Quadratische Funktionen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 3: | Zeile 3: | ||
{{Lösung versteckt| 1= Was bedeuten die Variable <math> x </math> und <math> f(x) </math>? Wofür sind sie Platzhalter? | 2= Tipp 1| 3= schließen}} | {{Lösung versteckt| 1= Was bedeuten die Variable <math> x </math> und <math> f(x) </math>? Wofür sind sie Platzhalter? | 2= Tipp 1| 3= schließen}} | ||
{{Lösung versteckt| 1= Wenn du die x-Koordinate | {{Lösung versteckt| 1= Wenn du die x-Koordinate eines Punktes in eine Funktion einsetzt, berechnest du so seine y-Koordinate. | 2= Tipp 2| 3=schließen}} | ||
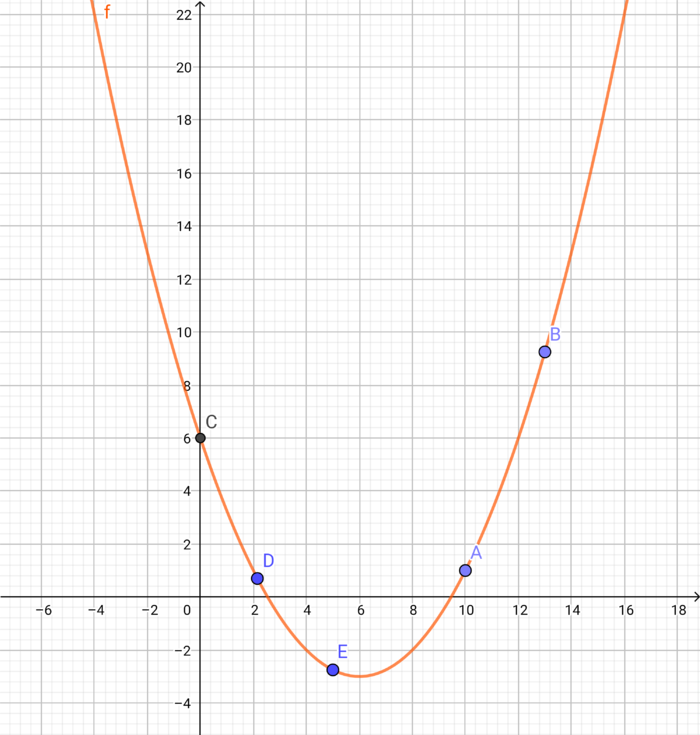
''' b) ''' Zeichne den Graphen der Funktion f mit den oben genannten Punkte nun in dein Heft. <br /><br /> | ''' b) ''' Zeichne den Graphen der Funktion f mit den oben genannten Punkte nun in dein Heft. <br /><br /> | ||
| Zeile 20: | Zeile 20: | ||
}} |Arbeitsmethode | }} |Arbeitsmethode | ||
}} | }} | ||
{{Box|Berechnung von Nullstellen| | |||
Gegeben seien folgende Funktionen: <br /> | |||
<math> g(x) = - 1 \cdot (x-8)^2+4 </math> <br /> | |||
<math> h(x) = 5x^2-6x-8</math> <br /> | |||
Berechne von beiden Funktionen jeweils die Nullstellen. | |||
{{Lösung versteckt| 1= Denke über die Bedeutung einer Nullstelle nach. Was bedeutet es, wenn eine Funktion an einem Punkt eine Nullstelle besitzt? |2= Tipp 1|3=schließen}} | |||
{{Lösung versteckt|1= Ein Punkt wird als Nullstelle einer Funktion bezeichnet, wenn seine '''y-Koordinate gleich 0''' ist. <br /> | |||
D.h. um die Nullstellen einer Funktion zu bestimmen, solltest du die Funktion gleich 0 setzen. <br /> | |||
Für die nächsten Schritte gibt es verschiedene Möglichkeiten vorzugehen: | |||
Ist deine Funktion in Scheitelpunktform, so hilft es dir den Term <math> (x-d) ^2</math> auf einer Seite zu isolieren, um dann die Wurzel ziehen zu können. <br /> | |||
Ansonsten gibt es als Hilfsmittel noch die dir bereits bekannte '''pq-Formel''' oder '''quadratische Ergänzung'''. |2=Tipp 2|3=schließen | |||
}} |Arbeitsmethode}} | |||
Version vom 28. Oktober 2019, 14:20 Uhr