Benutzer:Lena H. WWU-5/Quadratische Funktionen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
(Die Seite wurde neu angelegt: „{{Box|Berechne Die x- bzw. die y-Koordinate der Punkte, sodass diese auf der Funktion f liegen.|Gegeben sei die Funktion <math>f(x) =\frac {1} {4} \cdot (x-6)^…“) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 14: | Zeile 14: | ||
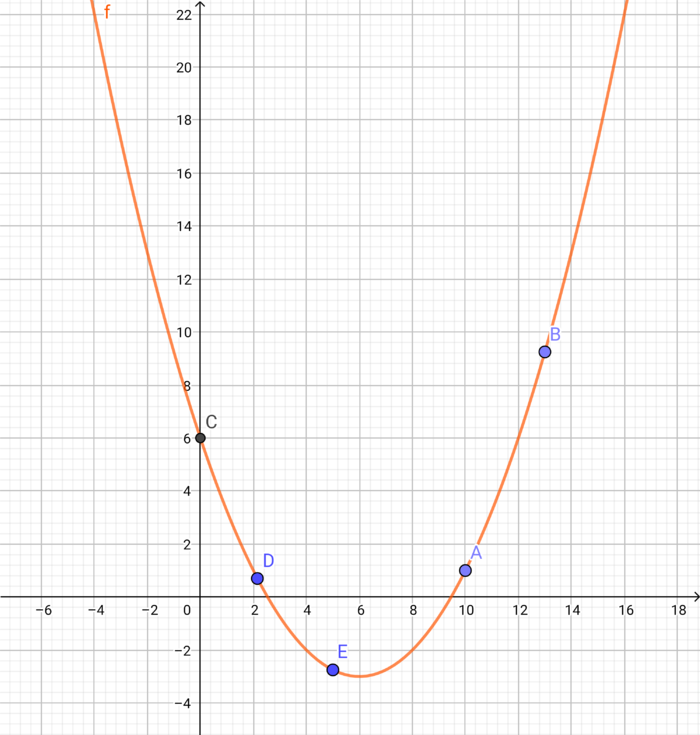
{{Lösung versteckt | 1= Die Punkte besitzen, um auf der Funktion <math> f(x) </math> zu liegen, folgende Koordinaten: <br /> | {{Lösung versteckt | 1= Die Punkte besitzen, um auf der Funktion <math> f(x) </math> zu liegen, folgende Koordinaten: <br /> | ||
<math>A=(10|1),, B=(13|\frac {29} {4}, C=(0|5), D=(\frac{43} {20}|\frac{7}{10} </math> und <math>E=(5|\frac{11} {4} </math>| 2=Lösung zu a) | 3= schließen}} | <math>A=(10|1),, B=(13|\frac {29} {4}, C=(0|5), D=(\frac{43} {20}|\frac{7}{10} </math> und <math>E=(5|-\frac{11} {4} </math>| 2=Lösung zu a) | 3= schließen}} | ||
{{Lösung versteckt |1= Wenn deine Zeichnung wie folgt aussieht, dann hast du alles richtig gemacht: |2=Lösung b) |3=schließen | {{Lösung versteckt |1= Wenn deine Zeichnung wie folgt aussieht, dann hast du alles richtig gemacht: [[Datei: Lösung Aufgabe 3.png|700px | zentriert]] |2=Lösung b) |3=schließen | ||
}} |Arbeitsmethode | }} |Arbeitsmethode | ||
}} | }} | ||