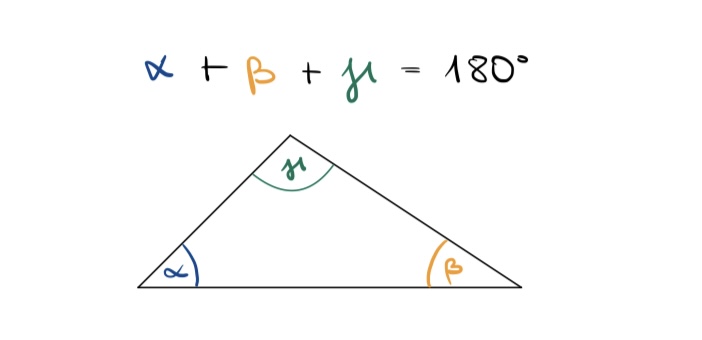|
|
| Zeile 31: |
Zeile 31: |
| |3=Definition}} | | |3=Definition}} |
| == Aufgabe 1 == | | == Aufgabe 1 == |
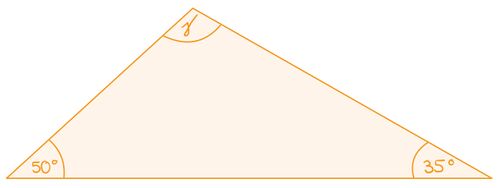
| {{Box |Level 1: Grundlagen der Innenwinkelsumme - Berechnung eines Winkels im Dreieck | Ein Dreieck hat die Winkel
| |
| 50° und 60°. Berechne den fehlenden Winkel und überprüfe, ob die Innenwinkelsumme des Dreiecks
| |
| 180° ergibt. | Arbeitsmethode | Farbe={{Farbe|orange}} }}
| |
| {{Lösung versteckt|1=
| |
| Die Innenwinkelsumme eines Dreiecks beträgt immer 180°.
| |
| Addiere die beiden gegebenen Winkel.
| |
| Subtrahiere die Summe von 180°, um den fehlenden Winkel zu berechnen.
| |
| 2=Tipp|3=Tipp verbergen}}
| |
| {{Lösung versteckt|1=
| |
| Gegebene Winkel: 50°, 60°.
| |
| Berechnung: 50°+60°+x=180° x=180°−50°−60°=70°
| |
| Fehlender Winkel: 70°.
| |
| |2=Lösung|3=Lösung verbergen}}
| |
|
| |
| {{Box | Level 2:=== '''Level 2: Kombination von Innenwinkelsumme und Stufenwinkel''' ===
| |
| '''Aufgabe:'''
| |
|
| |
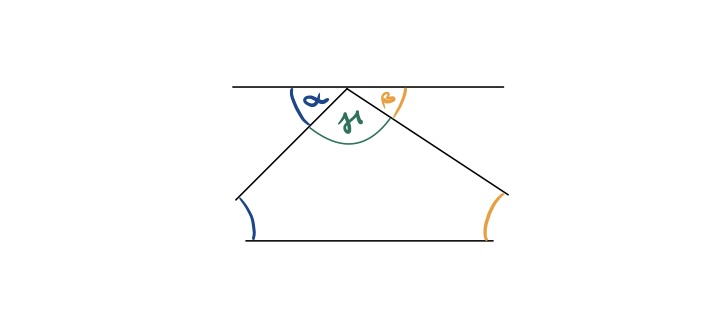
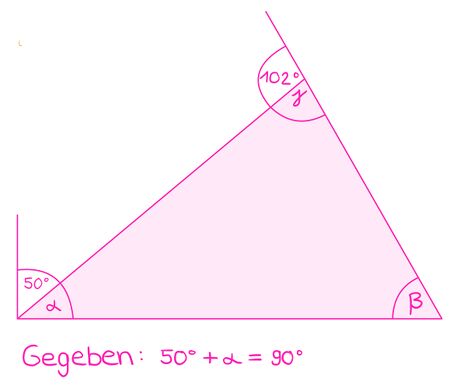
| Ein Dreieck liegt zwischen zwei parallelen Linien. Ein Außenwinkel des Dreiecks beträgt 120° und ein Innenwinkel beträgt 40°.
| |
|
| |
| # Berechne den zweiten Innenwinkel des Dreiecks mit Hilfe der Stufenwinkel-Regel.
| |
| # Berechne den dritten Innenwinkel des Dreiecks und überprüfe, ob die Innenwinkelsumme 180° ergibt.
| |
| # Zeichne das Dreieck (Maßstab nicht notwendig). | Arbeitsmethode | Farbe=#CD2990 }}
| |
| {{Lösung versteckt|1='''Tipps:'''
| |
|
| |
| * Nutze die '''Stufenwinkel-Regel''': Wenn zwei Linien parallel sind, sind die Stufenwinkel gleich.
| |
| * Berechne den zweiten Innenwinkel mithilfe der Stufenwinkel.
| |
| * Verwende die Innenwinkelsumme, um den dritten Winkel zu berechnen.
| |
| 2=Tipp|3=Tipp verbergen}}
| |
| {{Lösung versteckt|1=In einem gleichschenkligen Dreieck sind die beiden Basiswinkel gleich. Hier beträgt jeder der beiden Basiswinkel 65°. Um den Spitzenwinkel x zu berechnen, nutzen wir wieder die Innenwinkelsumme eines Dreiecks, die stets 180° beträgt.
| |
| Rechnung:
| |
|
| |
| Die Summe der beiden Basiswinkel beträgt:
| |
| 65°+65°=130°
| |
|
| |
| Der Spitzenwinkel x ergibt sich aus:
| |
| x=180°−130°=50°
| |
| Der Winkel an der Spitze ist 50°.
| |
|
| |
| Nachweis der Innenwinkelsumme:
| |
| 65°+65°+50°=180°
| |
| Damit ist die Innenwinkelsumme des Dreiecks rechnerisch bestätigt.
| |
|
| |
|
| |
| Warum ist die Summe immer 180°?
| |
| Die Innenwinkelsumme eines Dreiecks beträgt immer 180°, weil die drei Innenwinkel zusammen eine gerade Linie ergeben, wenn man die Winkel nebeneinander legt. Dies folgt aus den geometrischen Eigenschaften von Dreiecken:
| |
|
| |
|
| |
| Definition von Winkeln und Linien: Ein gerader Winkel entspricht 180°.
| |
| Geometrische Herleitung: Wenn man in einem Dreieck eine der Seiten verlängert, bildet der äußere Winkel zusammen mit dem Innenwinkel an der Basis einen geraden Winkel (180°). Alle Innenwinkel summieren sich daher ebenfalls zu 180°. Egal, wie ein Dreieck geformt ist (spitzwinklig, rechtwinklig, stumpfwinklig), bleibt diese Eigenschaft bestehen, da sie auf den geometrischen Grundlagen basiert.|2=Lösung|3=Lösung verbergen}}
| |
|
| |
| {{Box | Level 3: Das letzte Rätsel |Auf dem letzten Teil eurer Jagd entdeckt ihr eine mysteriöse geometrische Nachricht: "In jedem Dreieck steht ein gestreckter Winkel, wenn man die Innenwinkel nebeneinanderlegt." Ihr sollt dies überprüfen, in dem ihr ein eigenes Dreieck konstruiert und die drei Innenwinkel nebeneinander anordnet. Zeigt, dass diese Winkel zusammen einen gestreckten Winkel (180°) ergeben und begründet rechnerisch und logisch, warum dies immer so ist.
| |
| Zusatzfrage: Überlegt, ob diese Regel auch für Vierecke gilt und begründet eure Antwort. |Arbeitsmethode}}
| |
|
| |
| {{Lösung versteckt|1=Überlegt euch, wie ihr ein Vieleck in Dreiecke zerlegen könnt. Jedes Dreieck hat eine Innenwinkelsumme von
| |
| 180°. Die Anzahl der Dreiecke im Vieleck hilft euch dabei, die gesamte Innenwinkelsumme zu berechnen. Probiert es zuerst mit einem Viereck: Wie viele Dreiecke könnt ihr darin erkennen? Dann versucht es mit einem Fünfeck. Die Formel, die euch helfen könnte, lautet: (n−2)⋅180°, wobei n die Anzahl der Ecken des Vielecks ist.|2=Tipp 1|3=Tipp1 verbergen}}
| |
| {{Lösung versteckt|1=Hauptaufgabe: Nachweis der Innenwinkelsumme von 180° im Dreieck
| |
|
| |
| Konstruktion eines eigenen Dreiecks: Nehmen wir ein Dreieck mit den Innenwinkeln 50°, 60° und 70°.
| |
| Legt die drei Winkel nebeneinander, sodass sie eine gemeinsame Ecke haben. Wenn ihr die Winkel so arrangiert, bilden sie zusammen eine gerade Linie, also einen gestreckten Winkel von 180°.
| |
|
| |
| Rechnung:50°+60°+70°=180°
| |
|
| |
| Die Innenwinkelsumme eines Dreiecks ergibt sich aus der Geometrie von ebenen Flächen.
| |
| Ein Dreieck ist die einfachste geschlossene Form in der Ebene. Wenn man alle drei Innenwinkel nebeneinander legt, decken sie zusammen 180° ab, was der Definition eines gestreckten Winkels entspricht.
| |
|
| |
|
| |
| Zusatzfrage: Gilt diese Regel auch für Vierecke?
| |
| Nein, für Vierecke gilt diese Regel nicht direkt, da die Innenwinkelsumme eines Vierecks 360° beträgt.
| |
|
| |
| Warum 360°? Ein Viereck kann in zwei Dreiecke unterteilt werden, und die Innenwinkelsumme eines Dreiecks ist 180°. Daher ergibt sich für ein Viereck: 180°+180°=360°
| |
| Begründung: Die Anzahl der Innenwinkel in einem Polygon bestimmt die Summe der Winkel. Für ein n-Eck gilt die Formel: Innenwinkelsumme=(n−2)⋅180°
| |
| Für ein Viereck (n=4) ergibt sich: (4−2)⋅180°=360°|2=Lösung|3=Lösung verbergen}}
| |
|
| |
|
| |
|
|
| |
|