Geometrie im Dreieck/Triangle-Architects: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (28 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{Box | {{Box | ||
| 1 = Info | | 1 = Info | ||
| 2 = In diesem Lernpfadkapitel lernst du | | 2 = In diesem Lernpfadkapitel lernst du drei Kongruenzsätze kennen, wie du Konstruktionsbeschreibungen erstellst und umsetzt. | ||
Für die Bearbeitung dieses Kapitels benötigst du das [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Arbeitsblatt "Triangle Architects", einen Zirkel, ein Geodreieck und einen Bleistift. | Für die Bearbeitung dieses Kapitels benötigst du das [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Arbeitsblatt "Triangle Architects", einen Zirkel, ein Geodreieck und einen Bleistift. | ||
| Zeile 17: | Zeile 17: | ||
}} | }} | ||
==1. Achim und Alberta auf Burg Hülshoff == | |||
[[Datei:Achimalbertaa.png|thumb|Achim und Alberta sind verwirrt|284x284px]][[Datei:Schloss.png|thumb|Burg Hülshoff mit der Bühnenkonstruktion von Achim und Alberta|300px|links]] | |||
Zwischen Münster und Havixbeck steht die Burg Hülshoff. Vor etwa 200 Jahren wurde dort Annette Droste-Hülshoff geboren. Sie schrieb unter anderem das Gedicht "der Knabe im Moor". Zur Erinnerung an sie soll in den Burghof eine Bühne gebaut werden. Damit wurde das Architektenduo Achim-Alberta beauftragt. Das Duo hat bereits eine Idee und eine Skizze angefertigt (siehe Bilder). Heute wollen sie zum Schloss fahren und messen, wie groß die Bühne wird. Sie überlegen, welche Längen und Winkel sie messen müssen, um die Bühne genau zu konstruieren. [[Datei:Bühne1.png|thumb|Abbildung 3: Bühnenkonstruktion von Achim und Alberta |links]] | |||
Kannst du ihnen helfen? Welche Größen müssen Sie messen, um die Bühne zu konstruieren? Beschäftige dich dabei zunächst nur mit der dreieckigen Grundfläche (Siehe Abbildung 3). Notiere dir die Größen, die sie deiner Meinung nach messen müssen, auf einem Schmierpapier. Gibt es verschiedene Kombinationen, die eine '''Konstruktion''' möglich machen? In den folgenden Aufgaben lernst du, welche Größen ein Architekt braucht, um ein Dreieck zu konstruieren. Bei Aufgabe 4 kannst du dich selber überprüfen. | |||
{{Lösung versteckt|1=Messbare Größen sind die Länge der Hausseite a, der Hausseite b und der Hausseite c und die Größe der Winkel α, β und γ |2= Hilfe|3= Hilfe verbergen}} | |||
''' | |||
|2= | |||
==2. Ein Dreieck konstruieren mit Seite-Winkel-Seite (SWS)== | |||
==2. Ein Dreieck konstruieren mit Seite Winkel Seite (SWS)== | |||
In diesem Kapitel lernst du, wie du ein Dreieck '''konstruieren''' kannst, wenn du die Länge von zwei Seiten und den dazwischen liegenden Winkel kennst. In der Box steht eine Anleitung, die dir das Konstruieren von Dreiecken erleichtert. Nutze die Anleitung für die folgenden Aufgaben. | In diesem Kapitel lernst du, wie du ein Dreieck '''konstruieren''' kannst, wenn du die Länge von zwei Seiten und den dazwischen liegenden Winkel kennst. In der Box steht eine Anleitung, die dir das Konstruieren von Dreiecken erleichtert. Nutze die Anleitung für die folgenden Aufgaben. | ||
| Zeile 56: | Zeile 46: | ||
{{Lösung versteckt|1='''Konstruieren''' bedeutet, dass du eine geometrische Figur Schritt für Schritt erstellst. Dabei musst du sehr genau arbeiten. | {{Lösung versteckt|1='''Konstruieren''' bedeutet, dass du eine geometrische Figur Schritt für Schritt erstellst. Dabei musst du sehr genau arbeiten. | ||
'''Planfigur:''' Eine Planfigur ist eine kleine Zeichnung, in der noch nicht alle Längen, Winkel und Größen richtig eingetragen sind. Du markierst dir die gegebene Größen, Winkel, Seiten bunt und hast dadurch einen besseren Überblick. | '''Planfigur:''' Eine Planfigur ist eine kleine Zeichnung, in der noch nicht alle Längen, Winkel und Größen richtig eingetragen sind. Du markierst dir die gegebene Größen, Winkel, Seiten bunt und hast dadurch einen besseren Überblick. Ein Beispiel für eine Planfigur siehst du bei Aufgabe 2.3 | ||
'''Konstruktionsbeschreibung:''' Du schreibst in kleinen Schritten auf, wie du ein Dreieck gezeichnet hast. | '''Konstruktionsbeschreibung:''' Du schreibst in kleinen Schritten auf, wie du ein Dreieck gezeichnet hast. | ||
| Zeile 62: | Zeile 52: | ||
{{Box|Aufgabe 2.1: Konstruktionsbeschreibung anfertigen | {{Box|Aufgabe 2.1: Konstruktionsbeschreibung anfertigen| | ||
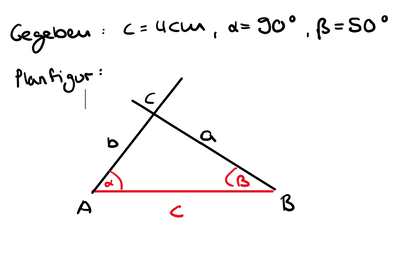
Du sollst ein Dreieck mit b <math> = </math> 2cm, α <math> = </math> 50°, c <math> = </math> 5cm konstruieren. Sortiere welche Schritte der Konstruktionsbeschreibung zu welchen Bildern gehören. | Du sollst ein Dreieck mit b <math> = </math> 2cm, α <math> = </math> 50°, c <math> = </math> 5cm konstruieren. Sortiere welche Schritte der Konstruktionsbeschreibung zu welchen Bildern gehören. Wenn du meinst, dass du die richtige Lösung gefunden hast, tippe auf den blauen Haken unten rechts. | ||
{{LearningApp|app=p6jdottyc24|width=100%|height=400px}} | {{LearningApp|app=p6jdottyc24|width=100%|height=400px}} | ||
|Arbeitsmethode | |||
| Farbe = {{Farbe|gelb}} | | Farbe = {{Farbe|gelb}} | ||
}} | }} | ||
{{Box|Aufgabe 2.2: Konstruktionsbeschreibung sortieren| | {{Box|Aufgabe 2.2: Konstruktionsbeschreibung sortieren|Du sollst wie zuvor ein Dreieck mit b <math> = </math> 2cm, α <math> = </math> 50°, c <math> = </math> 5cm konstruieren. Sortiere die Schritte in die richtige Reihenfolge. Benutze Aufgabe 2.1 als Hilfe. Wenn du meinst, dass du die richtige Lösung gefunden hast, tippe auf den blauen Haken unten rechts. | ||
Du sollst wie zuvor ein Dreieck mit b <math> = </math> 2cm, α <math> = </math> 50°, c <math> = </math> 5cm konstruieren. Sortiere die Schritte in die richtige Reihenfolge. Benutze Aufgabe 1 als Hilfe. | {{LearningApp|app=p2iyc69xk24|width=100%|height=400px}}|Arbeitsmethode | ||
{{LearningApp|app=p2iyc69xk24|width=100%|height=400px | |||
| Farbe = {{Farbe|gelb}} | | Farbe = {{Farbe|gelb}} | ||
}} | }} | ||
{{Box|Aufgabe 2.3: Fertigstellen einer Konstruktion mit SWS|{{Lösung versteckt | | {{Box|Aufgabe 2.3: Fertigstellen einer Konstruktion mit SWS|{{Lösung versteckt | | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] Konstruiere das Dreieck mit SWS. Gegeben sind b <math> = </math> 5cm, c <math> = </math> 9cm und α <math> = </math> 55°. | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Konstruiere das Dreieck mit SWS. Gegeben sind b <math> = </math> 5cm, c <math> = </math> 9cm und α <math> = </math> 55°. Achim und Alberta haben mit der Konstruktion schon begonnen. Stelle die Konstruktion auf dem '''Arbeitsblatt '''"Triangle Architects" fertig. Um deine Lösung zu überprüfen, kannst du die Länge der Seite a messen und mit der Musterlösung vergleichen. | ||
[[Datei:SWS 2 Planfigur.png|thumb|Planfigur für Aufgabe 2.3|400 px| center]] | [[Datei:SWS 2 Planfigur.png|thumb|Planfigur für Aufgabe 2.3|400 px| center]] | ||
{{Lösung versteckt|1=[[Datei:SWS 2 Lösung.png|thumb|Lösung für Aufgabe 2.3|400 px| center]] |2= Lösung|3= Lösung verbergen}} | {{Lösung versteckt|1=[[Datei:SWS 2 Lösung.png|thumb|Lösung für Aufgabe 2.3|400 px| center]] |2= Lösung|3= Lösung verbergen}} | ||
| Zeile 85: | Zeile 73: | ||
{{Box|Aufgabe 2.4: Durchführung einer Konstruktion mit SWS|{{Lösung versteckt | | {{Box|Aufgabe 2.4: Durchführung einer Konstruktion mit SWS|{{Lösung versteckt | | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] Konstruiere das Dreieck mit SWS auf dem '''Arbeitsblatt'''. Gegeben sind b <math> = </math> 8cm, c <math> = </math> 3cm und α <math> = </math> 80°. Führe dazu alle Schritte A-D durch. | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Konstruiere das Dreieck mit SWS auf dem '''Arbeitsblatt'''. Gegeben sind b <math> = </math> 8cm, c <math> = </math> 3cm und α <math> = </math> 80°. Führe dazu alle Schritte A-D durch. Um deine Lösung zu überprüfen, kannst du die Länge der Seite a messen und mit der Musterlösung vergleichen. | ||
{{Lösung versteckt|1=[[Datei:SWS 3 Lösung.png|thumb|Lösung für Aufgabe 2.4|400 px| center]] |2= Lösung|3= Lösung verbergen}} | {{Lösung versteckt|1=[[Datei:SWS 3 Lösung.png|thumb|Lösung für Aufgabe 2.4|400 px| center]] |2= Lösung|3= Lösung verbergen}} | ||
| Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode | | Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode | ||
| Zeile 98: | Zeile 86: | ||
}} | }} | ||
==3. Ein Dreieck konstruieren mit Winkel Seite Winkel (WSW)== | ==3. Ein Dreieck konstruieren mit Winkel-Seite-Winkel (WSW)== | ||
In diesem Kapitel lernst du, wie du ein Dreieck konstruieren kannst, wenn du zwei Winkel gegeben hast sowie die Seite, die zwischen diesen beiden Winkeln liegt. | In diesem Kapitel lernst du, wie du ein Dreieck konstruieren kannst, wenn du zwei Winkel gegeben hast sowie die Seite, die zwischen diesen beiden Winkeln liegt. | ||
| Zeile 115: | Zeile 103: | ||
}} | }} | ||
{{Box|Aufgabe 3.1: Konstruktionsbeschreibung anfertigen/ Bilder ordnen | {{Box|Aufgabe 3.1: Konstruktionsbeschreibung anfertigen/ Bilder ordnen| | ||
Du sollst ein Dreieck mit c <math> = </math> 5cm, α <math> = </math> 55°, β <math> = </math> 30° konstruieren. Ordne die Schritte der Konstruktionsbeschreibung den Bildern zu | Du sollst ein Dreieck mit c <math> = </math> 5cm, α <math> = </math> 55°, β <math> = </math> 30° konstruieren. Ordne die Schritte der Konstruktionsbeschreibung den Bildern zu. Wenn du meinst, dass du die richtige Lösung gefunden hast, tippe auf den blauen Haken unten rechts. | ||
{{LearningApp|app=proeom3x324|width=100%|height=400px}} | {{LearningApp|app=proeom3x324|width=100%|height=400px}} | ||
|Arbeitsmethode | |||
| Farbe = {{Farbe|gelb}} | | Farbe = {{Farbe|gelb}} | ||
}} | }} | ||
{{Box|Aufgabe 3.2: Konstruktionsbeschreibung anfertigen/ Lückentext | {{Box|Aufgabe 3.2: Konstruktionsbeschreibung anfertigen/ Lückentext| | ||
Du sollst ein Dreieck mit c <math> = </math> 4cm, α <math> = </math> 50°, β <math> = </math> 40° konstruieren. Fülle die Lücken im Text in der richtigen Reihenfolge aus. | Du sollst ein Dreieck mit c <math> = </math> 4cm, α <math> = </math> 50°, β <math> = </math> 40° konstruieren. Fülle die Lücken im Text in der richtigen Reihenfolge aus. Wenn du meinst, dass du die richtige Lösung gefunden hast, tippe auf den blauen Haken unten rechts. | ||
{{LearningApp|app=p23jg55dn24|width=100%|height=500px}} | {{LearningApp|app=p23jg55dn24|width=100%|height=500px}} | ||
{{Lösung versteckt|1=Beschränke dich bei der Auswahl der Texte für die Lücken auf folgende Optionen: | {{Lösung versteckt|1=Beschränke dich bei der Auswahl der Texte für die Lücken auf folgende Optionen: | ||
| Zeile 132: | Zeile 120: | ||
c = 4cm. | c = 4cm. | ||
|2=Hilfen|3=Hilfe verbergen}} | |2=Hilfen|3=Hilfe verbergen}} | ||
|Arbeitsmethode | |||
| Farbe = {{Farbe|gelb}} | | Farbe = {{Farbe|gelb}} | ||
}} | }} | ||
| Zeile 147: | Zeile 135: | ||
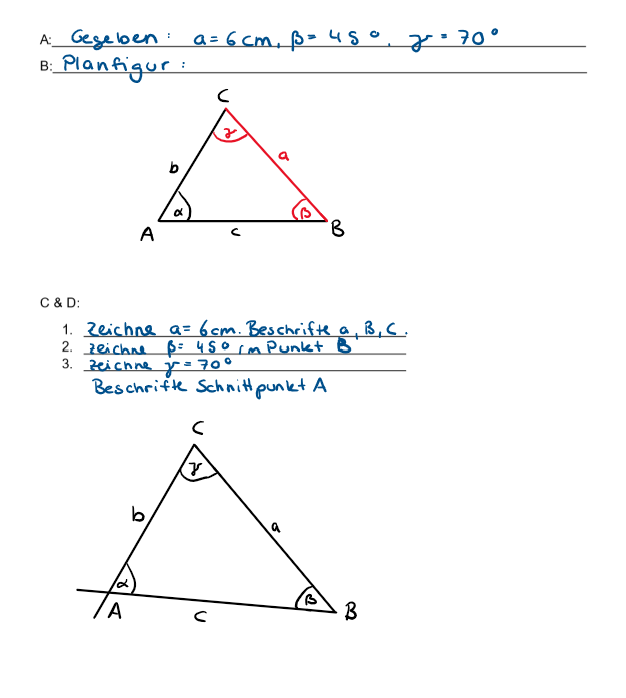
{{Box|Aufgabe 3.4: Dachkonstruktion mit WSW|{{Lösung versteckt | | {{Box|Aufgabe 3.4: Dachkonstruktion mit WSW|{{Lösung versteckt | | ||
Achim und Alberta möchten ein dreieckiges Dach bauen. Leider sind sie vergesslich und wissen nur noch die Größen von 2 Winkeln und die dazwischenliegende Seitenlänge. Konstruiere das dreieckige Dach mit SWS. Gegeben sind a <math> = </math> 6cm, 𝝱 <math> = </math> 450 und ɣ <math> = </math> 70°. Führe dazu alle Schritte A-D '''in deinem Heft''' durch. | Achim und Alberta möchten ein dreieckiges Dach bauen. Leider sind sie vergesslich und wissen nur noch die Größen von 2 Winkeln und die dazwischenliegende Seitenlänge. Konstruiere das dreieckige Dach mit SWS. Gegeben sind a <math> = </math> 6cm, 𝝱 <math> = </math> 450 und ɣ <math> = </math> 70°. Führe dazu alle Schritte A-D '''in deinem Heft''' durch. | ||
{{Lösung versteckt|1=[[Datei:WSW 3.4 Lösung.png|thumb|Lösung für Aufgabe 3.4| | {{Lösung versteckt|1=[[Datei:WSW 3.4 Lösung.png|thumb|Lösung für Aufgabe 3.4|800 px| center]] |2= Lösung|3= Lösung verbergen}} | ||
| Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode | | Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode | ||
| Farbe = #CD2990 | | Farbe = #CD2990 | ||
| Zeile 154: | Zeile 142: | ||
==4. Training macht den Meister== | ==4. Training macht den Meister== | ||
{{Box|Aufgabe 4.1: Trainiere dein Wissen!| | {{Box|Aufgabe 4.1: Trainiere dein Wissen!|Nach einer stressigen Woche haben die Architekten Achim und Alberta einige Dinge über die Konstruktion von Dreiecken vergessen. Hilf ihnen, sich wieder an dieses Wissen zu erinnern und beantworte die folgenden Fragen. Dabei wählst du aus verschiedenen Antworten die richtige aus, oder entscheidest, ob eine Behauptung richtig oder falsch ist! Klicke davor auf den Button "Alleine spielen"! | ||
Nach einer stressigen Woche haben die Architekten Achim und Alberta einige Dinge über die Konstruktion von Dreiecken vergessen. Hilf ihnen, sich wieder an dieses Wissen zu erinnern und beantworte die folgenden Fragen. Dabei wählst aus verschiedenen Antworten die richtige aus, oder entscheidest, ob eine Behauptung richtig oder falsch ist! Klicke davor auf den Button "Alleine spielen"! | |||
{{LearningApp|app=pnvmzmsb224|width=100%|height=400px | {{LearningApp|app=pnvmzmsb224|width=100%|height=400px}}|Arbeitsmethode | ||
| Farbe = {{Farbe|gelb}} | | Farbe = {{Farbe|gelb}} | ||
}} | }} | ||
{{Box|Aufgabe 4.2: Erinnere dich an den Einstieg zurück!| | {{Box|Aufgabe 4.2: Erinnere dich an den Einstieg zurück!| | ||
Achim und Alberta wollen eine dreieckige Bühne konstruieren. Welche Größen müssen sie messen, um die Bühne zu konstruieren? Fülle den Lückentext aus. | Achim und Alberta wollen eine dreieckige Bühne konstruieren. Welche Größen müssen sie messen, um die Bühne zu konstruieren? Fülle den Lückentext aus. | ||
[[Datei:Bühne1.png|thumb|Bühnenkonstruktion von Achim und Alberta |rechts]] | [[Datei:Bühne1.png|thumb|Bühnenkonstruktion von Achim und Alberta |rechts]] | ||
| Zeile 183: | Zeile 168: | ||
Hofseite c und die Winkel α und β | Hofseite c und die Winkel α und β | ||
|2=Lösung|3=Lösung verbergen}} | |2=Lösung|3=Lösung verbergen}} | ||
|Arbeitsmethode | |||
| Farbe = {{Farbe|gelb}} | | Farbe = {{Farbe|gelb}} | ||
}} | }} | ||
Super, du bist mit dem normalen Teil fertig! Wenn du möchtest kannst du das 5. Thema "Triangle-Experts" bearbeiten, ansonsten gehe zurück zur Startseite [[Geometrie im Dreieck|Geometrie im Dreieck]] und bearbeite ein weiteres Kapitel! | |||
==5. Triangle-Experts: Kann man mit drei Seiten immer ein Dreieck konstruieren?== | ==5. Triangle-Experts: Kann man mit drei Seiten immer ein Dreieck konstruieren?== | ||
Nach dem Trainingslager sind Achim und Alberta nun in der Lage, sich schwereren Aufgaben zu widmen. Die beiden haben dummerweise ihr Werkzeug zum Winkelmessen vergessen. Nun überlegen die beiden, ob es ausreicht, nur die drei Seitenlängen zu kennen, um ein Dreieck zu konstruieren. Achim sagt: "Klar, das ist doch leicht, habe ich drei Seiten gegeben, dann kann ich immer ein Dreieck konstruieren!" Alberta hingegen zögert etwas: "Ich bin mir da nicht so sicher, ich glaube, dass die Seitenlängen besondere Voraussetzungen erfüllen müssen!" Bearbeite die folgenden Aufgaben und finde heraus, wer Recht hat! | |||
{{Box|Aufgabe 5.1: Wann ist ein Dreieck konstruierbar?|{{Lösung versteckt | | {{Box|Aufgabe 5.1: Wann ist ein Dreieck konstruierbar?|{{Lösung versteckt | | ||
Unten siehst du ein Dreieck. Du kannst das Dreieck verändern, indem du die Längen der Seiten a,b und c mithilfe des jeweiligen Schiebereglers veränderst. | Unten siehst du im GeoGebra-Applet ein Dreieck. Du kannst das Dreieck verändern, indem du die Längen der Seiten a,b und c mithilfe des jeweiligen Schiebereglers veränderst. | ||
'''a)''' Überprüfe zuerst ob die folgende Dreiecke mit den gegebenen Seiten konstruierbar sind. | '''a)''' Überprüfe zuerst ob die folgende Dreiecke mit den gegebenen Seiten konstruierbar sind. | ||
| Zeile 198: | Zeile 185: | ||
# a<math> = </math>4, b<math> = </math>9, c<math> = </math>4 | # a<math> = </math>4, b<math> = </math>9, c<math> = </math>4 | ||
{{Lösung versteckt|1=[[Datei:SeiteSeiteSeite.png|thumb|Wie du hier sehen kannst, lassen sich die 3. und 4. Möglichkeit nicht konstruieren, da sich die beiden Schenkel nicht berühren|800 px| center]] | |||
|2= Lösung|3= Lösung verbergen}} | |||
'''b)''' Finde nun durch Bewegen der Schieberegler heraus, unter welchen Bedingungen ein Dreieck mit drei gegebenen Seiten a,b und c konstruierbar ist. Bei Aufgabe 5.2 kannst du deine Theorie überprüfen. | |||
{{Lösung versteckt|1= Addiere jeweils die Länge von 2 Seiten. Ist diese Summe kleiner oder größer als die dritte Seite? | {{Lösung versteckt|1= Addiere jeweils die Länge von 2 Seiten. Ist diese Summe kleiner oder größer als die dritte Seite? | ||
|2=Tipp zu Aufgabe 1b|3=Tipp verbergen}} | |2=Tipp zu Aufgabe 1b|3=Tipp verbergen}} | ||
<ggb_applet id="PdRUrDxe" width="1000" height="601" border="888888" /> | |||
| Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode | | Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode | ||
| Farbe = #5E43A5 | | Farbe = #5E43A5 | ||
| Zeile 209: | Zeile 199: | ||
{{Box|Aufgabe 5.2: Entscheide, was richtig ist|{{Lösung versteckt | | {{Box|Aufgabe 5.2: Entscheide, was richtig ist|{{Lösung versteckt | | ||
Kreuze an, welche Bedingungen in einem Dreieck vorliegen müssen, damit es konstruierbar ist. Wähle alle richtigen Antworten aus! | Kreuze an, welche Bedingungen in einem Dreieck vorliegen müssen, damit es konstruierbar ist. Wähle alle richtigen Antworten aus! Wenn du meinst, dass du die richtige Lösung gefunden hast, tippe auf den blauen Haken unten rechts. | ||
{{LearningApp|app=pkzd58un324|width=100%|height=400px}} | {{LearningApp|app=pkzd58un324|width=100%|height=400px}} | ||
| Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode | | Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode | ||
| Zeile 215: | Zeile 205: | ||
}} | }} | ||
{{Box| | {{Box|Stelle einen Merksatz auf!|{{Lösung versteckt | | ||
Fülle den Lückentext aus, indem du aus den Vorschlägen das richtige Wort in die jeweilige Lücke setzt. Schreibe dann den ausgefüllten Text | Fülle den Lückentext aus, indem du aus den Vorschlägen das richtige Wort in die jeweilige Lücke setzt. Wenn du meinst, dass du die richtige Lösung gefunden hast, tippe auf den blauen Haken unten rechts. Schreibe dann den ausgefüllten Text in dein Heft. | ||
{{LearningApp|app=ph0i4nnut24|width=100%|height=350px}} | {{LearningApp|app=ph0i4nnut24|width=100%|height=350px}} | ||
| Aufgabe anzeigen | Aufgabe verbergen}}| | | Aufgabe anzeigen | Aufgabe verbergen}}|Merksatz | ||
| Farbe = #5E43A5 | | Farbe = #5E43A5 | ||
}} | }} | ||
Super, du bist fertig! Gehe zurück zur Startseite | Super, du bist fertig! Gehe zurück zur Startseite und bearbeite ein weiteres Kapitel! | ||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Geometrie_im_Dreieck}} | |||
Aktuelle Version vom 4. Dezember 2024, 14:26 Uhr
Info
1. Achim und Alberta auf Burg Hülshoff
Zwischen Münster und Havixbeck steht die Burg Hülshoff. Vor etwa 200 Jahren wurde dort Annette Droste-Hülshoff geboren. Sie schrieb unter anderem das Gedicht "der Knabe im Moor". Zur Erinnerung an sie soll in den Burghof eine Bühne gebaut werden. Damit wurde das Architektenduo Achim-Alberta beauftragt. Das Duo hat bereits eine Idee und eine Skizze angefertigt (siehe Bilder). Heute wollen sie zum Schloss fahren und messen, wie groß die Bühne wird. Sie überlegen, welche Längen und Winkel sie messen müssen, um die Bühne genau zu konstruieren.
Kannst du ihnen helfen? Welche Größen müssen Sie messen, um die Bühne zu konstruieren? Beschäftige dich dabei zunächst nur mit der dreieckigen Grundfläche (Siehe Abbildung 3). Notiere dir die Größen, die sie deiner Meinung nach messen müssen, auf einem Schmierpapier. Gibt es verschiedene Kombinationen, die eine Konstruktion möglich machen? In den folgenden Aufgaben lernst du, welche Größen ein Architekt braucht, um ein Dreieck zu konstruieren. Bei Aufgabe 4 kannst du dich selber überprüfen.
2. Ein Dreieck konstruieren mit Seite-Winkel-Seite (SWS)
In diesem Kapitel lernst du, wie du ein Dreieck konstruieren kannst, wenn du die Länge von zwei Seiten und den dazwischen liegenden Winkel kennst. In der Box steht eine Anleitung, die dir das Konstruieren von Dreiecken erleichtert. Nutze die Anleitung für die folgenden Aufgaben.
Konstruieren bedeutet, dass du eine geometrische Figur Schritt für Schritt erstellst. Dabei musst du sehr genau arbeiten.
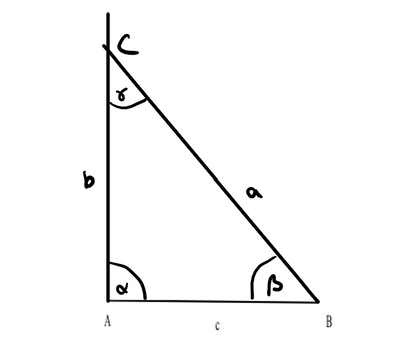
Planfigur: Eine Planfigur ist eine kleine Zeichnung, in der noch nicht alle Längen, Winkel und Größen richtig eingetragen sind. Du markierst dir die gegebene Größen, Winkel, Seiten bunt und hast dadurch einen besseren Überblick. Ein Beispiel für eine Planfigur siehst du bei Aufgabe 2.3
Konstruktionsbeschreibung: Du schreibst in kleinen Schritten auf, wie du ein Dreieck gezeichnet hast.
3. Ein Dreieck konstruieren mit Winkel-Seite-Winkel (WSW)
In diesem Kapitel lernst du, wie du ein Dreieck konstruieren kannst, wenn du zwei Winkel gegeben hast sowie die Seite, die zwischen diesen beiden Winkeln liegt.
4. Training macht den Meister
Super, du bist mit dem normalen Teil fertig! Wenn du möchtest kannst du das 5. Thema "Triangle-Experts" bearbeiten, ansonsten gehe zurück zur Startseite Geometrie im Dreieck und bearbeite ein weiteres Kapitel!
5. Triangle-Experts: Kann man mit drei Seiten immer ein Dreieck konstruieren?
Nach dem Trainingslager sind Achim und Alberta nun in der Lage, sich schwereren Aufgaben zu widmen. Die beiden haben dummerweise ihr Werkzeug zum Winkelmessen vergessen. Nun überlegen die beiden, ob es ausreicht, nur die drei Seitenlängen zu kennen, um ein Dreieck zu konstruieren. Achim sagt: "Klar, das ist doch leicht, habe ich drei Seiten gegeben, dann kann ich immer ein Dreieck konstruieren!" Alberta hingegen zögert etwas: "Ich bin mir da nicht so sicher, ich glaube, dass die Seitenlängen besondere Voraussetzungen erfüllen müssen!" Bearbeite die folgenden Aufgaben und finde heraus, wer Recht hat!
Super, du bist fertig! Gehe zurück zur Startseite und bearbeite ein weiteres Kapitel!