Benutzer:Jonte Uni MS 14/Entwurf: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(11 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 25: Zeile 25:




<div class="box experimentieren">
== Basiswissen ==
Der Kreis, der alle '''Eckpunkte''' eines Dreiecks berührt, heißt '''Umkreis'''. Der '''Umkreismittelpunkt''' ist der Schnittpunkt der drei '''Mittelsenkrechten''' des Dreiecks. Zur Konstruktion des Umkreises genügt es, zwei Mittelsenkrechten zu konstruieren.
<ggb_applet id="ek99gmjh" width="700" height="450" />


Der Kreis, der alle '''Seiten''' eines Dreiecks genau einmal berührt, heißt '''Inkreis'''. Der '''Inkreismittelpunkt''' ist der Schnittpunkt der drei '''Winkelhalbierenden''' des Dreiecks. Auch hier genügen zwei Winkelhalbierende zur Konstruktion des Kreises.
<ggb_applet id="fae77shu" width="700" height="450" />
Der '''Schwerpunkt''' eines Kreises ist der Punkt auf dem das Dreieck balanciert werden kann. Er liegt auf dem Schnittpunkt der '''Seitenhalbierenden'''. Auf einer Seitenhalbierenden liegt der Schwerpunkt immer auf 2/3 der Strecke vom Eckpunkt bis zur gegenüberliegenden Seite.
<ggb_applet id="anh5rdnm" width="700" height="450" />
</div>




== Wiederholung ==
{{Box|1=Wiederholung: Umkreis- und Inkreismittelpunkt und Schwerpunkt eines Dreiecks|2=In Kapitel 3 (Aufgabe 4) habt ihr den Standort eines Hochseilgartens ermittelt, der von den drei Städten Münster, Paderborn und Bielefeld den gleichen Abstand haben soll. Dafür habt ihr den Schnittpunkt der Mittelsenkrechten ermittelt. Der Schnittpunkt der Mittelsenkrechten, hat von allen drei Eckpunkten des Dreiecks den gleichen Abstand und wird auch als '''Umkreismittelpunkt''' bezeichnet.
<ggb_applet id="x7krntjr" width="100%" height="100%" />


Zusätzlich habt ihr in Kapitel 3 die Winkelhalbierenden wiederholt. Die Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt, der als '''Inkreismittelpunkt''' des Dreiecks bezeichnet wird. Der Inkreismittelpunkt hat von allen drei Seiten des Dreiecks den gleichen Abstand.
(Geogebra Applet)


Als weiteren wichtigen Punkt in einem Dreieck habt ihr den '''Schwerpunkt''' kennengelernt. Der Schwerpunkt ist der Schnittpunkt der Seitenhalbierenden. Auf einer Seitenhalbierenden liegt der Schwerpunkt immer auf 2/3 der Strecke vom Eckpunkt bis zur gegenüberliegenden Seite.
 
(GeoGebra Applet) }}
 
 


==Aufgabe 1==
==Aufgabe 1==
{{Box | Aufgabe 1: | In einem Naturschutzgebiet kreuzen sich die drei Wanderwege a, b und c und bilden ein Dreieck. Es soll ein neuer Brunnen gebaut werden, der für Wanderer von allen drei Wegen gleich gut erreichbar ist. An welchem Punkt im Dreieck sollte der Brunnen gebaut werden, damit der Abstand zu jedem Wanderweg gleich ist? | Arbeitsmethode | Farbe={{Farbe|orange}} }}
{{Box | Aufgabe 1:| Experimentiere mit den Besonderen Punkten des Dreiecks herum und notiere dir die besonderen Eigenschaften auf dem Arbeitsblatt.| Arbeitsmethode | Farbe={{Farbe|orange}} }}
<ggb_applet id="ek99gmjh" width="700" height="450" />
{{Lösung versteckt|
Der Umkreis berührt alle Eckpunkte eines Dreiecks. Der Umkreismittelpunkt ist der Schnittpunkt der drei Mittelsenkrechten des Dreiecks. Zur Konstruktion des Umkreises genügt es, zwei Mittelsenkrechten zu zeichnen.
|Eigenschaften anzeigen|Eigenschaften verbergen}}
<ggb_applet id="fae77shu" width="700" height="450" />
{{Lösung versteckt|
Der Inkreis berührt Seiten eines Dreiecks genau einmal. Der Inkreismittelpunkt ist der Schnittpunkt der drei Winkelhalbierenden des Dreiecks. Zur Konstruktion des Inkreises genügt es, zwei Winkelhalbierende zu zeichnen.
|Eigenschaften anzeigen|Eigenschaften verbergen}}
<ggb_applet id="anh5rdnm" width="700" height="450" />
{{Lösung versteckt|
Der Schwerpunkt ist der Schnittpunkt der drei Seitenhalbierenden des Dreiecks. Diese teilt er immer im Verhältnis 2:1. Zur Konstruktion des Schwerpunkts genügt es, zwei Seitenhalbierende zu zeichnen.
|Eigenschaften anzeigen|Eigenschaften verbergen}}
</div>
 
 


==Aufgabe 2==
==Aufgabe 2==
Zeile 80: Zeile 82:
{{Box|1=Eigenschaften des Umkreismittelpunkt|2=Der Umkreismittelpunkt kann als einziger Punkt auch außerhalb des Dreiecks liegen. Nämlich genau dann, wenn das Dreieck einen stumpfen Winkel hat. Bei einem rechtwinkligen Dreieck liegt der Umkreismittelpunkt auf der gegebüberliegenden Seite (Hypotenuse). Im Kasten kannst du die Eckpunkte des Dreiecks verschieben und den Umkreismittelpunkt beobachten.
{{Box|1=Eigenschaften des Umkreismittelpunkt|2=Der Umkreismittelpunkt kann als einziger Punkt auch außerhalb des Dreiecks liegen. Nämlich genau dann, wenn das Dreieck einen stumpfen Winkel hat. Bei einem rechtwinkligen Dreieck liegt der Umkreismittelpunkt auf der gegebüberliegenden Seite (Hypotenuse). Im Kasten kannst du die Eckpunkte des Dreiecks verschieben und den Umkreismittelpunkt beobachten.
Wenn du nicht mehr weißt was ein stumpfer Winkel ist schaue [https://projekte.zum.de/wiki/Digitale_Werkzeuge_in_der_Schule/Rund_ums_Dreieck hier].  
Wenn du nicht mehr weißt was ein stumpfer Winkel ist schaue [https://projekte.zum.de/wiki/Digitale_Werkzeuge_in_der_Schule/Rund_ums_Dreieck hier].  
<ggb_applet id="krn9wqhf" width="400" height="450" /> }}
<ggb_applet id="krn9wqhf" width="400" height="450" />  
 
}}
 
==Aufgabe 2==
{{Box | Aufgabe 2:| Notiere zu jedem besonderen Punkt des Dreiecks die Kerneigenschaften.| Arbeitsmethode | Farbe={{Farbe|orange}} }}
{{Lösung versteckt|
 
Der Inkreismittelpunkt hat zu allen Seiten den gleichen Abstand.
 
Der Umkreismittelpunkt hat zu allen Eckpunkten den gleichen Abstand.
 
Der Schwerpunkt liegt immer auf 2/3 der Strecke vom Eckpunkt bis zur gegenüberliegenden Seite.
|Tipp anzeigen|Tipp verbergen}}


==Aufgabe 3==
==Aufgabe 3==
{{Box | Aufgabe 3:  | Benenne die Punkte M<sub>1</sub> M<sub>2</sub> und M<sub>3</sub> der dynamischen Grafik. Du kannst die Eckpunkte des Dreiecks bewegen. | Arbeitsmethode}}
{{Box | Aufgabe 3:  | Benenne die Punkte M<sub>1</sub> M<sub>2</sub> und M<sub>3</sub> der dynamischen Grafik. Du kannst die Eckpunkte des Dreiecks bewegen. | Arbeitsmethode }}
<ggb_applet id="srjcpuge" width="400" height="450" />
<ggb_applet id="srjcpuge" width="400" height="450" />
<div class="lueckentext-quiz">
<div class="lueckentext-quiz">
Zeile 103: Zeile 94:
</div>
</div>


{{Lösung versteckt|Du kannst den Umkreismittelpunkt herausfinden in dem du einen stumpfen Winkel im Dreieck erzeugst. Dann liegt der Umkreismittelpunkt außerhalb des Dreiecks. Wenn du nicht mehr weißt was ein stumpfer Winkel ist schaue [https://projekte.zum.de/wiki/Digitale_Werkzeuge_in_der_Schule/Rund_ums_Dreieck hier] .|Tipp anzeigen|Tipp verbergen}}
{{Lösung versteckt|Du kannst den Umkreismittelpunkt herausfinden in dem du einen stumpfen Winkel im Dreieck erzeugst. Dann liegt der Umkreismittelpunkt außerhalb des Dreiecks. Wenn du nicht mehr weißt was ein stumpfer Winkel ist schaue [https://projekte.zum.de/wiki/Digitale_Werkzeuge_in_der_Schule/Rund_ums_Dreieck hier] .|Tipp 1 anzeigen|Tipp 1 verbergen}}
{{Lösung versteckt|Überlege dir, wo beispielsweise eine Winkelhalbierende entlangläuft und verschieben dann einen Eckpunkt. Der Inkreismittelpunkt ist der Schnittpunkt der Winkelhalbierenden.|Tipp 2 anzeigen|Tipp 2 verbergen}}
 
 
==Schnappe die Diebe==
{{Box|Aufgabe 4: Entfernungsproblem |Finde den Ort an dem Kommissar Biehl warten soll, damit er gleich schnell bei jedem möglichen Einbruchsort ist. Du kannst im Fenster mit Geogebra Konstruktionen durchführen.
<ggb_applet id="rpsnggh3" width="720" height="520" />
 
{{Lösung versteckt|Kommissar Biehl sollte von jedem Einbruchsort gleichweit entfernt sein.|2=Tipp 1|3=Hilfe verbergen}}
 
 
{{Lösung versteckt|Der Umkreismittelpunkt ist von jedem Eckpunkt eines Dreiecks gleich weit entfernt.|2=Tipp 2|3=Hilfe verbergen}}|Arbeitsmethode| Farbe = {{Farbe|orange}}
}}
 
Zur Übersicht: [[Geometrie im Dreieck]]

Aktuelle Version vom 12. November 2024, 12:15 Uhr

Kapitel-Informationskästchen

Info

In diesem Lernpfadkapitel werden besondere Punkte eines Dreiecks behandelt.

Bei diesen Punkten handelt es sich um den Umkreismittelpunkt, den Inkreismittelpunkt und den Schwerpunkt. Um dieses Kapitel bearbeiten zu können, müssen die Winkelhalbierende, die Seitenhalbierende und die Mittelsenkrechte eines Dreiecks konstruiert werden können. Wenn du das noch nicht beherrschst, schaue dir dieses Kapitel an (Link).

Bei den Aufgaben unterscheiden wir folgende Typen:

  • In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
  • Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
  • Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
Viel Erfolg!

Einstieg

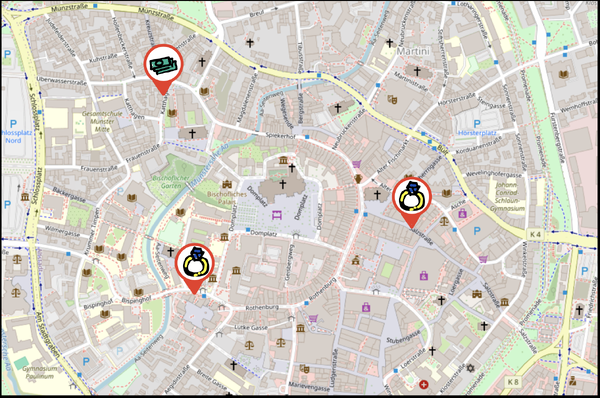
Karte mit den möglichen Einbrüchen.

Ganz Münster ist in Angst versetzt. Einbrecher sind in der Stadt unterwegs. Doch Kommissar Biehl hat eine heiße Spur: er weiß wo der nächste Einbruch stattfinden wird. Leider kommen dafür zwei Juweliere und eine Bank infrage.

Wo soll sich Kommissar Biehl auf die Lauer legen?

Kommissar Biehl muss natürlich schnellstmöglich vor Ort sein, um die Einbrecher auf frischer Tat zu ertappen. Wo soll er sich heute Nacht in der Stadt aufhalten, damit er schnell an jedem möglichen Einbruchsort sein kann?







Aufgabe 1

Aufgabe 1:
Experimentiere mit den Besonderen Punkten des Dreiecks herum und notiere dir die besonderen Eigenschaften auf dem Arbeitsblatt.
GeoGebra

Der Umkreis berührt alle Eckpunkte eines Dreiecks. Der Umkreismittelpunkt ist der Schnittpunkt der drei Mittelsenkrechten des Dreiecks. Zur Konstruktion des Umkreises genügt es, zwei Mittelsenkrechten zu zeichnen.

GeoGebra

Der Inkreis berührt Seiten eines Dreiecks genau einmal. Der Inkreismittelpunkt ist der Schnittpunkt der drei Winkelhalbierenden des Dreiecks. Zur Konstruktion des Inkreises genügt es, zwei Winkelhalbierende zu zeichnen.

GeoGebra

Der Schwerpunkt ist der Schnittpunkt der drei Seitenhalbierenden des Dreiecks. Diese teilt er immer im Verhältnis 2:1. Zur Konstruktion des Schwerpunkts genügt es, zwei Seitenhalbierende zu zeichnen.


Aufgabe 2

Aufgabe 1:

a) Ordne die Punkte den Geraden zu, deren Schnittpunkt sie bilden.

Mittelsenkrechte - Umkreismittelpunkt

Winkelhalbierende - Inkreismittelpunkt

Seitenhalbierende - Schwerpunkt

b) Wie kannst du dir gut merken, welcher Punkt zu welchen Geraden gehört? Notiere hierzu eine Eselsbrücke oder eine andere Merktechnik zu den drei Punkten.

Eine einfache Eselsbrücke könnte so lauten:

Schwerpunkt und Seitenhalbierende: Beides beginnt mit "S".

Inkreis und Winkelhalbierende: In beidem kommt "ink" vor.

Umkreis und Mittelsenkrechte: In beidem kommt "m" vor.



Wiederholung

Eigenschaften des Umkreismittelpunkt

Der Umkreismittelpunkt kann als einziger Punkt auch außerhalb des Dreiecks liegen. Nämlich genau dann, wenn das Dreieck einen stumpfen Winkel hat. Bei einem rechtwinkligen Dreieck liegt der Umkreismittelpunkt auf der gegebüberliegenden Seite (Hypotenuse). Im Kasten kannst du die Eckpunkte des Dreiecks verschieben und den Umkreismittelpunkt beobachten. Wenn du nicht mehr weißt was ein stumpfer Winkel ist schaue hier.

GeoGebra

Aufgabe 3

Aufgabe 3:
Benenne die Punkte M1 M2 und M3 der dynamischen Grafik. Du kannst die Eckpunkte des Dreiecks bewegen.
GeoGebra

Deine Lösung:

M1 - Umkreismittelpunkt, M2 - Schwerpunkt, M3 - Inkreismittelpunkt

Du kannst den Umkreismittelpunkt herausfinden in dem du einen stumpfen Winkel im Dreieck erzeugst. Dann liegt der Umkreismittelpunkt außerhalb des Dreiecks. Wenn du nicht mehr weißt was ein stumpfer Winkel ist schaue hier .
Überlege dir, wo beispielsweise eine Winkelhalbierende entlangläuft und verschieben dann einen Eckpunkt. Der Inkreismittelpunkt ist der Schnittpunkt der Winkelhalbierenden.


Schnappe die Diebe

Aufgabe 4: Entfernungsproblem

Finde den Ort an dem Kommissar Biehl warten soll, damit er gleich schnell bei jedem möglichen Einbruchsort ist. Du kannst im Fenster mit Geogebra Konstruktionen durchführen.

GeoGebra
Kommissar Biehl sollte von jedem Einbruchsort gleichweit entfernt sein.


Der Umkreismittelpunkt ist von jedem Eckpunkt eines Dreiecks gleich weit entfernt.

Zur Übersicht: Geometrie im Dreieck

Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Jonte_Uni_MS_14/Entwurf&oldid=99515“