Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Geometrische Figuren und Winkel/Koordinatensysteme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6 | Geometrische Figuren und Winkel
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 1: Einführung in das Koordinatensystem | | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 1: Einführung in das Koordinatensystem | | ||
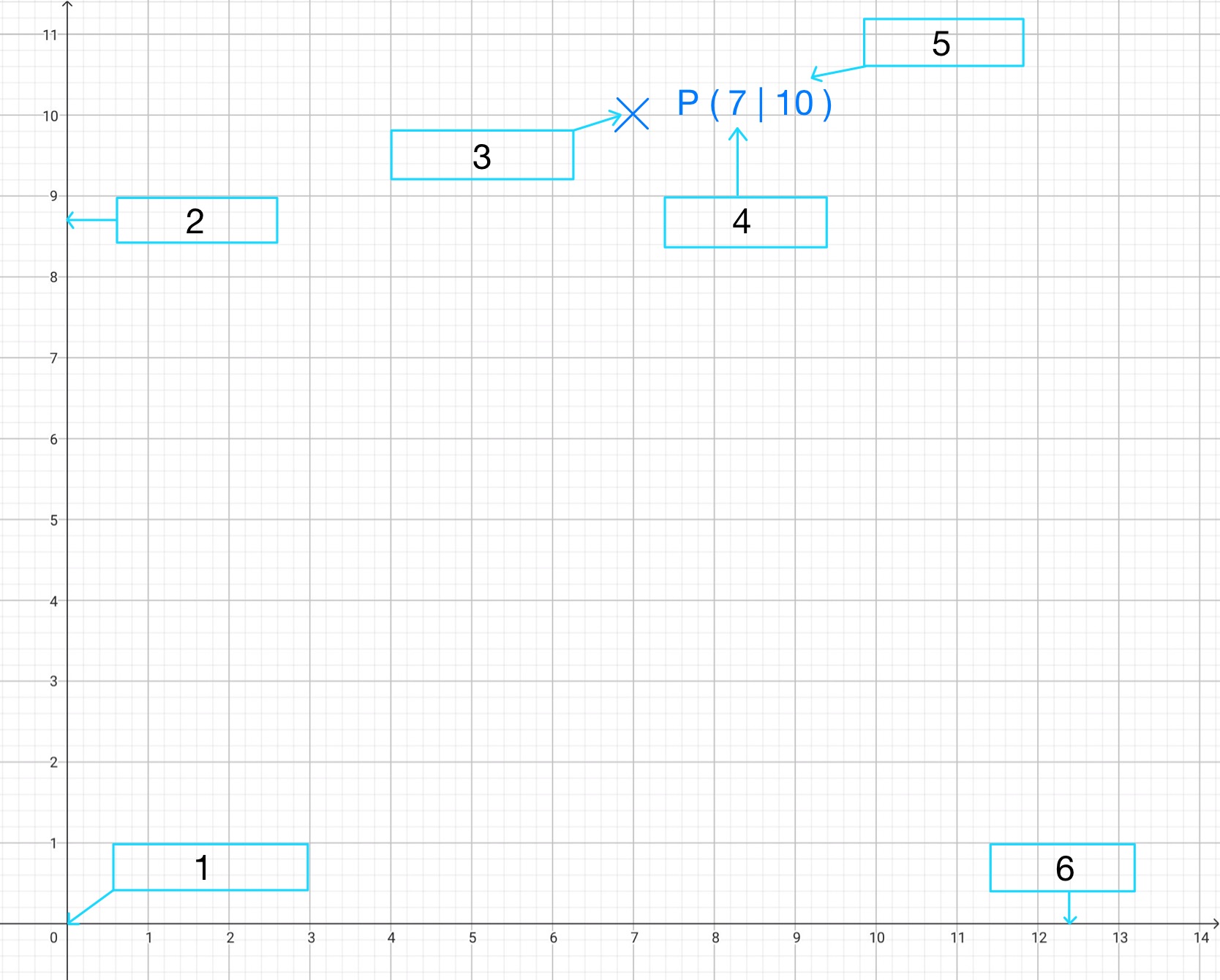
Beschrifte das Koordinatensystem mit den richtigen Begriffen! | Beschrifte das Koordinatensystem mit den richtigen Begriffen! | ||
[[Datei:Koordinatensystem beschriften.jpg| | [[Datei:Koordinatensystem beschriften.jpg|right]] | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{Kästchen 1 zeigt} | {'''Kästchen 1 zeigt'''} | ||
- die X-Achse | - die X-Achse | ||
- die Y-Achse | - die Y-Achse | ||
| Zeile 13: | Zeile 14: | ||
- einen Punkt | - einen Punkt | ||
{Kästchen 2 zeigt} | {'''Kästchen 2 zeigt'''} | ||
- die X-Achse | - die X-Achse | ||
+ die Y-Achse | + die Y-Achse | ||
| Zeile 21: | Zeile 22: | ||
- einen Punkt | - einen Punkt | ||
{Kästchen 3 zeigt} | {'''Kästchen 3 zeigt'''} | ||
- die X-Achse | - die X-Achse | ||
- die Y-Achse | - die Y-Achse | ||
| Zeile 29: | Zeile 30: | ||
+ einen Punkt | + einen Punkt | ||
{Kästchen 4 zeigt} | {'''Kästchen 4 zeigt'''} | ||
- die X-Achse | - die X-Achse | ||
- die Y-Achse | - die Y-Achse | ||
| Zeile 38: | Zeile 39: | ||
{Kästchen 5 zeigt} | {'''Kästchen 5 zeigt'''} | ||
- die X-Achse | - die X-Achse | ||
- die Y-Achse | - die Y-Achse | ||
| Zeile 46: | Zeile 47: | ||
- einen Punkt | - einen Punkt | ||
{Kästchen 6 zeigt} | {'''Kästchen 6 zeigt'''} | ||
+ die X-Achse | + die X-Achse | ||
- die Y-Achse | - die Y-Achse | ||
| Zeile 58: | Zeile 59: | ||
}} | }} | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: Beschriftung von Koordinatensystemen|In einem Koordinatensystem lässt sich die Lage eines Punktes genau angeben. Bei jedem Punkt '''P (x/y)''' wird zuerst die '''x-Koordinate''' und dann die '''y-Koordinate''' angegeben. | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: Beschriftung von Koordinatensystemen|In einem Koordinatensystem lässt sich die Lage eines Punktes genau angeben. Bei jedem Punkt '''P (x<math>\mid</math>y)''' wird zuerst die '''x-Koordinate''' und dann die '''y-Koordinate''' angegeben. | ||
Wichtig ist dabei der "Null-Punkt" (der '''Ursprung''') des Koordinatensystems. Damit ist derjenige Punkt gemeint, an dem sich die beiden Achsen schneiden, also der Punkt (0/0). | Wichtig ist dabei der "Null-Punkt" (der '''Ursprung''') des Koordinatensystems. Damit ist derjenige Punkt gemeint, an dem sich die beiden Achsen schneiden, also der Punkt (0<math>\mid</math>0). | ||
Die vier Bereiche in einem Koordinatensystem werden '''Quadranten''' genannt. Der erste Quadrant ist der Bereich oben rechts des Koordinatensystems und die anderen Bereiche werden gegen den Uhrzeigersinn durchnummeriert. Häufig wird nur der erste Quadrant gezeichnet.|Merksatz| Farbe = {{Farbe|grün}} | Die vier Bereiche in einem Koordinatensystem werden '''Quadranten''' genannt. Der erste Quadrant ist der Bereich oben rechts des Koordinatensystems und die anderen Bereiche werden gegen den Uhrzeigersinn durchnummeriert. Häufig wird nur der erste Quadrant gezeichnet.|Merksatz| Farbe = {{Farbe|grün}} | ||
}} | }} | ||
| Zeile 65: | Zeile 66: | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 2: Punkte im Koordinatensystem | | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 2: Punkte im Koordinatensystem | | ||
Bewege die Punkte an die angegebenen Koordinaten! | Bewege die Punkte an die angegebenen Koordinaten! | ||
<ggb_applet id="evvvrpxr" width="1000" height="685"/>|Aufgabe| Farbe = {{Farbe|orange}} | <ggb_applet id="evvvrpxr" width="1000" height="685"/> | ||
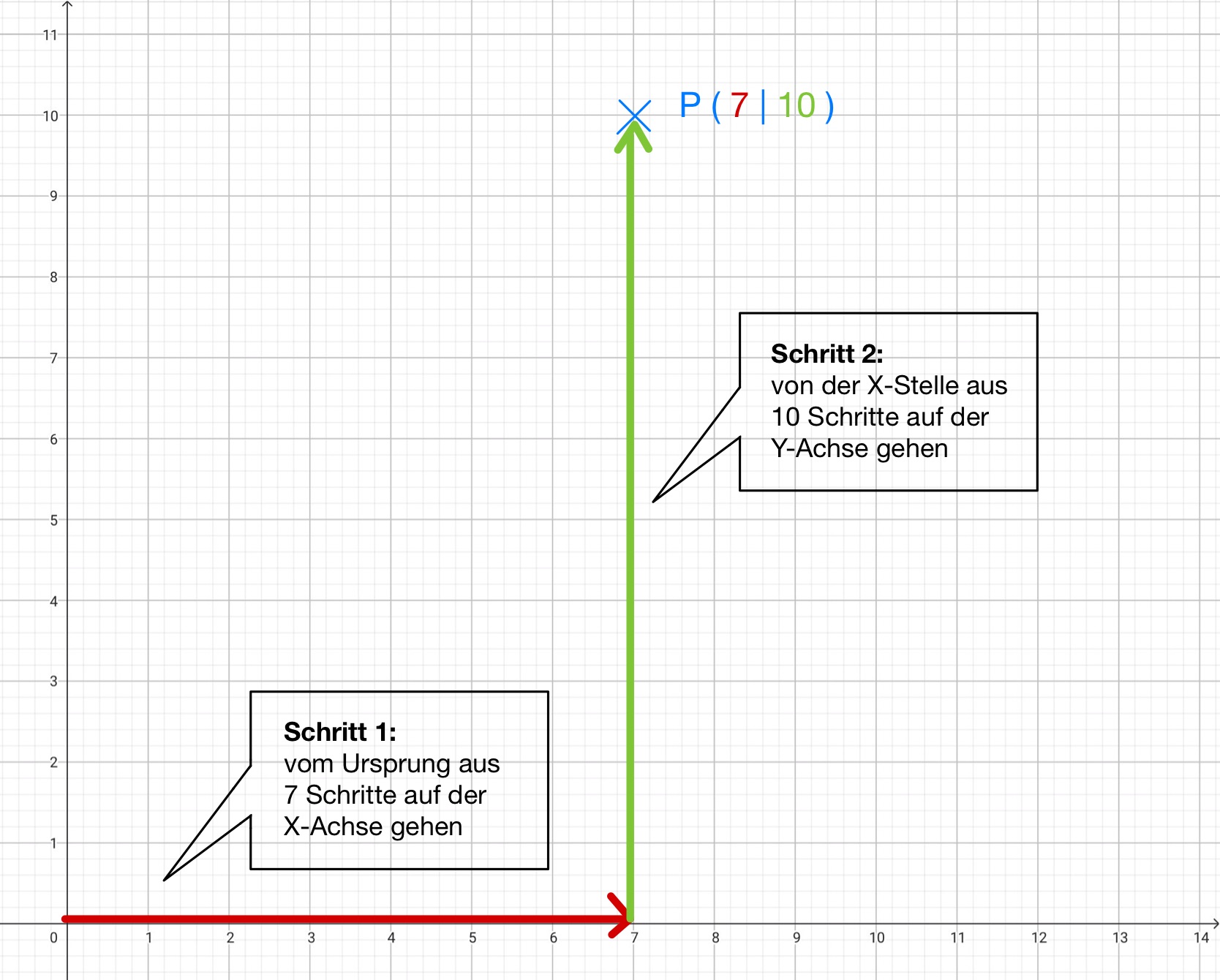
{{Lösung versteckt|1='''So trägst du Punkte in ein Koordinatensystem ein''':[[Datei:Punkte im Koordinatensystem eintragen-2.jpg|zentriert]] |2=Tipp |3=Tipp verbergen}} | |||
|Aufgabe| Farbe = {{Farbe|orange}} | |||
}} | }} | ||
| Zeile 73: | Zeile 76: | ||
}} | }} | ||
[[Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Geometrische Figuren und Winkel/Geraden, Strecken, Parallelen und Senkrechten|Nächstes Kapitel]] | |||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Kleine_Lernstandserhebung_zur_Doppeljahrgangsstufe_5/6}} | |||