Abitur Physik am Gymnasium Trittau/Atommodelle: Unterschied zwischen den Versionen
GT067 (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
GT067 (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 37: | Zeile 37: | ||
=== Orbital-Modell === | === Orbital-Modell === | ||
Das Orbital-Modell unterscheidet sich zu den bisherigen Modellen. Es beschreibt im dreidimensionalen Raum eine Aufenthaltswahrscheinlichkeit | [[Datei:Https---www.researchgate.net-figure-Atomic-s-orbital-and-three-orthogonal-p-orbitals fig1 236217213.png|mini]] | ||
Das Orbital-Modell unterscheidet sich zu den bisherigen Modellen es ist bis heute das genauste Modell. Es beschreibt im dreidimensionalen Raum eine Aufenthaltswahrscheinlichkeit eines Elektron. Diese Wahrscheinlichkeiten wurden erstmals von Erwin Schrödinger berechnet, mit Hilfe der Schrödinger Gleichung. Die Gleichung kann man nicht mit Schulmathematik lösen, weswegen häufig das Potenzialtopf-Modell zur Hilfe gezogen wird. Die Schrödinger-Gleichung berücksichtigt damit nicht nur die Dreidimensionalität, sondern auch den Welle-Teilchen Dualismus und die damit einhergehende "Unschärferelation" von Werner Heisenberg. Die Orbitale kann man sich wie Wolken vorstellen, die nach außen dünner werden. Die Wahrscheinlichkeit nimmt dort ab. | |||
Als Ergebnis der Schrödinger Gleichung erhält man bestimmte Funktionen der Energieniveaus. Um die Schrödinger-Gleichung von einem Wasserstoff Atom zu lösen benutzen wir den unendlich hohen Potenzial Topf. Die Funktionen in dem Topf sind stehende Wellen, das bedeutet es kann nur bestimme Energieniveaus als Lösung geben. Quadriert man die Funktion erhält man die Aufenthaltswahrscheinlichkeit. Die Energieniveaus sind abhängig von der Hauptquantenzahl. Damit ist sozusagen die Schale auf dem das Elektron sich befindet gemeint. Mit der Formel | |||
<math>E_n=(-R_H\times h \times c \times) \div n^2</math> können die verschiedenen Orbitale berechnet werden. | |||
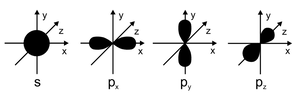
In der Abbildung sieht man die Anschauliche Darstellung. In einem Orbital können sich höchstens zwei Elektronen befinden. Das niedrigste Energieniveau besitzt das 1S Orbital. Je nach Anzahl der Elektronen werden die Orbitale Kombiniert. | |||
<references /> | |||
Aktuelle Version vom 22. Mai 2024, 20:15 Uhr
Atommodelle
Die wohl bekanntesten und wichtigsten Atommodelle, zu unserer Zeit sind wohl, die von Rutherford und Nils Bohr. Damit diese beiden Modelle entwickelt werden konnten machten sich bereits andere Physiker und Philosophen, in der Antike, Gedanken über die Zusammensetzung von Materie. Ganz geklärt wie Atome aufgebaut sind, ist bis heute nicht klar jedes Modell hat seine Schwächen.
Das Demokrit Modell
Die zwei griechischen Philosophen Leukipp und Demokrit erschlossen sich, durch reines nachdenken, dass Materie nicht unendlich teilbar sei. Sie stellten also die Theorie auf, dass Materie aus unteilbaren Atomen bestehe. Dadurch sind Atome auch benannt. Atomos kommt aus dem griechischen und bedeutet "unteilbar". Das Atom sei also das kleinste Teilchen, also der Grundbaustein von Materie. Nach dem Heutigen Kenntnisstand sind das Quarks und Leptonen.
Modell nach Dalton
1803 ergänzte John Dalton, die Vorstellung von Demokrit auf der Grundlage, des Gesetzes der konstanten Mengen Verhältnisse. Elemente bestanden aus unteilbaren Atomen die sich in Masse und Größe unterscheiden. Durch dieses erste konkrete Atommodell konnte L. Boltzmann Diffusion, Brown'sche Bewegung und Aggregatzustände erklären.
Das Rosinenkuchen Modell
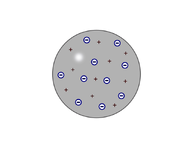
Der Physiker J.J. Thomson führte Experimente bei Gasentladung durch. Diese kann man mit dem heutigen bekannten Versuch, des Massensprektrometers, vergleichen. Ionen werden durch ein Elektrisches Feld beschleunigt und durch ein Magnetfeld geschossen. Durch die unterschiedliche Ablenkung kann man die Massen der Ionen bestimmen. Als Thomson herausfand, dass es Teilchen gab die noch eine kleinere Masse haben müssen als Atome und es positive und negative Ladung geben müsse stellte er das Thomson'sche Atommodell auf. Atome bestanden, nach ihm, aus negativ geladenen Elektronen, sowie positiv geladenen Teilchen, die gleichmäßig im Atom verteilt sind. Die Atome sind im gesamten neutral, können aber Ladung abgeben wodurch geladene Ionen entstehen. Es wird aufgrund der Ähnlichkeit auch Rosinenkuchen Modell genannt. Die genaue Vorstellung des inneren vom Atom kam von P. Lenard. Er schoss die Elektronen auf eine Aluminium Folie und nur wenige, die langsam waren kam nicht hindurch. Deshalb kam er zu dem Schluss das das innere zwar leer aber mit elektrischen Felder gefüllt sein müsse.
Rutherford'sche Atommodell
Rutherford führte ähnliche Experimente, wie Thomson durch. Er ersetzte die Ionen bzw. Elektronen durch Alphateilchen, diese wurden ebenfalls auf eine Metallfolie geschossen. Obwohl die Alphateilchen eine größere Masse als Elektronen haben wurden auch bei diesem Versuch nur wenige abgelenkt und falls sie abgelenkt wurden war der entsprechende Winkel nur zwischen 0° und 180°. Daraus ließ sich schließen, dass nicht die Elektronen Impulse auf einander ausübten, sondern eine größere Masse innerhalb des Atoms. Zusätzlich muss diese Masse kleiner sein als die Masse innerhalb der Atome aus der Metallfolie. Denn nach dem Impulserhaltungssatz, würden die Teilchen bei gleicher Masse stehen bleiben und bei Größerer die Atome aus der Folie schießen. Ernest Rutherford entwickelte also 1911 das sogenannte Planetenmodell. Seiner Vorstellung nach befindet sich die gesamte Masse des Atoms im positiven Kern. Seine Messungen ergaben für den Kern einen Durchmesser von 10^-14 m. Die gesamte negative Ladung, die Elektronen, kreisten in Ellipsen um den Kern.
Zwar konnten nun die Streuversuche erklärt werden, allerdings nicht die Stabilität von Atomen. Nach der klassischen Physik würden die Elektronen allerdings mit der Zeit Energie verlieren, denn sie senden elektromagnetische Wellen bei der Bewegung aus, und die Anziehungskraft des Kerns wäre stärker als sie Zentripetalkraft, die sie auf der Kreisbewegung halten würde. Als Folge würden die Atome zusammenfallen.
Das Bohr'sche Atommodell
Nils Bohr ergänzte 1913 das Atommodell von Rutherford um den Wiederspruch, des Zusammenfalls aufzulösen. Auch bei ihm kreisten, die Elektronen um den Kern. Damit die Zentripetalkraft aber nicht weniger wurde, stellte er Bedingungen mit Hilfe des planckschen Wirkungsquantum auf. Die sog. Bohr'schen Postulate. Zum einen befinden die Elektronen sich auf stabilen Bahnen ohne Photonen bzw. Energie abzugeben. Damit dies Möglich war mussten die Bahnen genau festgeschrieben sein. Sie werden mit n gekennzeichnet und Hauptquantenzahl genannt. Außerdem stellte Bohr eine Formel für den Bahndrehimpuls auf.
n=1,2,3,4,...
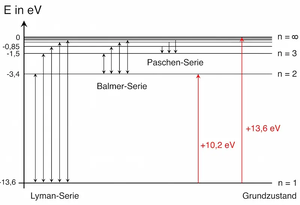
Außerdem legt er fest, inwiefern, beim Ionisieren, Energie abgegeben werden kann. Die Schalen besitzen unterschiedliche Energieniveau, sodass wenn ein Elektron eine Schale niedriger springt, Energie in Form von Photonen abgegeben wird. Die Energie des Photons ist gleich der Energiedifferenz der Schalen.
Bei der Aufstellung der Postulate ging Bohr vom Wasserstoffatom aus, von dem nun auch die Bahnradien und Geschwindigkeiten berechnet werden können. Man kann die Coulomb Kraft gleich der Zentripetalkraft setzten, denn die Coulomb Kraft ist die Kraft, welche die Elektronen zum Kern zieht sie muss also gleichgroß wie die entgegenwirkende Zentripetalkraft , die dafür sorgt, dass die Elektronen auf der Kreisbahn bleiben, sein. Durch umstellen der Gleichung erhält man den Radius, auch Bohr'schen Radius genannt, und die Bahngeschwindigkeit.
Nun kann auch die Energie der Bahnen berechnet werden, die mit beim Wasserstoff mit den Spektrallinien übereinstimmen. In einem Energieniveauschema kann man die jeweilige Energiedifferenz, die beim Sprung von Photonen absorbiert oder emittiert wird, ablesen. Obwohl mit dem Bohr'schen Atommodell weiterhin der Widerspruch der Elektronenbahnen bestand und die Annahmen von Bohr nur auf das Wasserstoff vollständig zu treffen, konnten nun die Spektrallinien erklärt werden, man konnte den Atom Radius abschätzen und Erkenntnisse über Absorption und Emission gewinnen.
Orbital-Modell
Das Orbital-Modell unterscheidet sich zu den bisherigen Modellen es ist bis heute das genauste Modell. Es beschreibt im dreidimensionalen Raum eine Aufenthaltswahrscheinlichkeit eines Elektron. Diese Wahrscheinlichkeiten wurden erstmals von Erwin Schrödinger berechnet, mit Hilfe der Schrödinger Gleichung. Die Gleichung kann man nicht mit Schulmathematik lösen, weswegen häufig das Potenzialtopf-Modell zur Hilfe gezogen wird. Die Schrödinger-Gleichung berücksichtigt damit nicht nur die Dreidimensionalität, sondern auch den Welle-Teilchen Dualismus und die damit einhergehende "Unschärferelation" von Werner Heisenberg. Die Orbitale kann man sich wie Wolken vorstellen, die nach außen dünner werden. Die Wahrscheinlichkeit nimmt dort ab.
Als Ergebnis der Schrödinger Gleichung erhält man bestimmte Funktionen der Energieniveaus. Um die Schrödinger-Gleichung von einem Wasserstoff Atom zu lösen benutzen wir den unendlich hohen Potenzial Topf. Die Funktionen in dem Topf sind stehende Wellen, das bedeutet es kann nur bestimme Energieniveaus als Lösung geben. Quadriert man die Funktion erhält man die Aufenthaltswahrscheinlichkeit. Die Energieniveaus sind abhängig von der Hauptquantenzahl. Damit ist sozusagen die Schale auf dem das Elektron sich befindet gemeint. Mit der Formel
können die verschiedenen Orbitale berechnet werden.
In der Abbildung sieht man die Anschauliche Darstellung. In einem Orbital können sich höchstens zwei Elektronen befinden. Das niedrigste Energieniveau besitzt das 1S Orbital. Je nach Anzahl der Elektronen werden die Orbitale Kombiniert.