Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Geometrische Figuren und Winkel/Geraden, Strecken, Parallelen und Senkrechten: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6 | Geometrische Figuren und Winkel
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (49 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Geraden, Strecken, Parallelen und Senkrechten == | == Geraden, Strecken, Parallelen und Senkrechten == | ||
=== Geraden und Strecken === | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 1: Eigenschaften von Geraden und Strecken|Was macht eine Gerade aus und was macht eine Strecke aus? Ordne die Eigenschaften und Bilder zu! | |||
{{LearningApp|app=paux0magj21|width=100%|height|600px}}|Aufgabe | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: Geraden und Strecken| | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz| | |||
Eine '''Gerade''' ist eine gerade Linie, die durch mehrere Punkte gehen kann. Sie hat weder Start- noch Endpunkt, ist also unendlich, und kann deshalb nie vollständig gezeichnet werden. Sie wird mit kleinen Buchstaben, wie g oder h bezeichnet. | Eine '''Gerade''' ist eine gerade Linie, die durch mehrere Punkte gehen kann. Sie hat weder Start- noch Endpunkt, ist also unendlich, und kann deshalb nie vollständig gezeichnet werden. Sie wird mit kleinen Buchstaben, wie g oder h bezeichnet. | ||
[[Datei:Gerade.png|1000px]] | [[Datei:Gerade.png|1000px]] | ||
Eine '''Strecke''' ist eine gerade Linie, die zwischen zwei Punkten verläuft. Sie hat also einen Startpunkt und einen Endpunkt und kann also vollständig gezeichnet werden. Sie wird mit <math>\overline{AB}</math> oder <math>\overline{CD}</math> usw. bezeichnet. | Eine '''Strecke''' ist eine gerade Linie, die zwischen zwei Punkten verläuft. Sie hat also einen Startpunkt und einen Endpunkt und kann also vollständig gezeichnet werden. Sie wird mit <math>\overline{AB}</math> oder <math>\overline{CD}</math> usw. bezeichnet. | ||
[[Datei:Strecke.png|1000px]] | [[Datei:Strecke.png|1000px]] | ||
|Merksatz | |Merksatz|Farbe = {{Farbe|grün}}}} | ||
{{ | |||
=== Senkrechten und Parallelen === | |||
'''Zur Erinnerung:''' | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: senkrecht und parallel| | |||
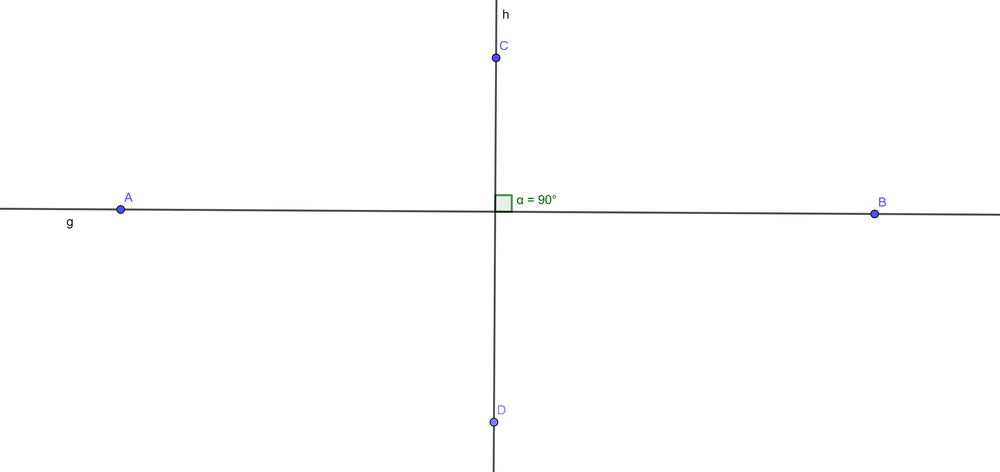
Zwei Geraden g und h heißen zueinander '''senkrecht''' ("orthogonal"), wenn sie einen rechten Winkel bilden (90°). | |||
Wir schreiben g <math>\bot</math> h | |||
[[Datei:Senkrechte.png|ohne|mini|1000px]] | |||
Zwei Geraden g und h heißen zueinander '''parallel''', wenn alle Punkte auf g denselben Abstand von h haben und umgekehrt. | |||
Wir schreiben: g <math>\mid</math><math>\mid</math> h | |||
[[Datei:Parallele.png|ohne|mini|1000px]] | |||
|Merksatz|Farbe = {{Farbe|grün}}}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 2: Senkrecht oder parallel?|Entscheide, welche Geraden zueinander senkrecht und welche zueinander parallel sind! | |||
{{LearningApp|app=prqofp7nc21 |width=100%|heigth=900px}} | |||
| Farbe=#CD2990 | |||
}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (***) Aufgabe 3 : Geraden, Strecken, Senkrechten und Parallelen zeichnen | |||
| 2 = [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Nutze für diese Aufgabe das Koordinatensystem auf dem Arbeitsblatt unter Aufgabe 3 und antworte dann hier im Lernpfad! | |||
a) Zeichne folgende Punkte im Koordinatensystem auf dem Arbeitsblatt ein: | |||
A (8<math>\mid</math>7) B (14<math>\mid</math>7) | |||
b) Verbinde die beiden Punkte nun mit der Strecke <math>\overline{AB}</math>. | |||
c) Zeichne nun eine parallele Gerade zu <math>\overline{AB}</math> im Abstand von fünf Längeneinheiten (Kästchen) und nenne sie g. | |||
d) Zeichne die kürzeste Verbindung vom Punkt A zur Gerade g ein. Beschrifte den Schnittpunkt auf der Gerade g mit D. | |||
e) Zeichne die kürzeste Verbindung vom Punkt B zur Gerade g ein. Beschrifte den Schnittpunkt auf der Gerade g mit C. | |||
f) Zeichne die Diagonalen ein. | |||
g) Zeichne eine zur Diagonale <math>\overline{AC}</math> senkrechte Strecke ein, welche im Punkt A startet und drei Längeneinheiten (Kästchen) lang ist. | |||
h) Zeichne eine zur Diagonale <math>\overline{BD}</math> senkrechte Strecke ein, welche im Punkt B startet und drei Längeneinheiten (Kästchen) lang ist. | |||
< | |||
i) Nenne den Punkt, in dem sich die beiden neuen Strecken treffen E. | |||
j) Was ist entstanden? | |||
<quiz display="simple"> | |||
{ } | |||
# | |||
- irgendeine komische Figur aus Geraden und Strecken | |||
- ein Rechteck | |||
+ das Haus vom Nikolaus | |||
- drei Quadrate | |||
</quiz> | |||
| 3 = Aufgabe | |||
|Farbe = #5E43A5 | |||
}} | |||
{{Lösung versteckt|1=Die kürzeste Verbindung zwischen einem Punkt und einer Gerade ist eine Senkrechte zur Gerade g.|2=Tipp zu d) und e)|3=Tipp 1 verbergen}} | |||
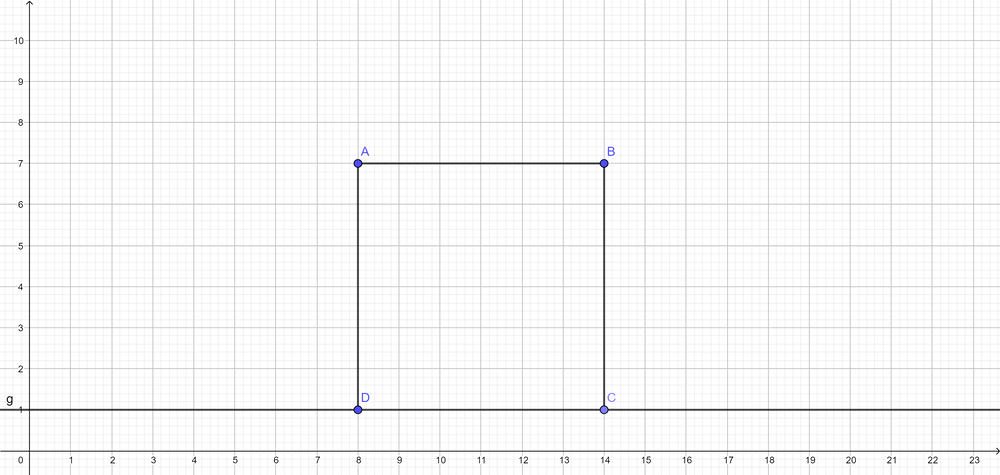
{{Lösung versteckt|1=So sollte deine Zeichnung nach e) aussehen: [[Datei:Aufgabe 3 Geraden Tipp 2.png|1000px]]|2=Lösung d) und e) |3=Lösung verbergen}} | |||
{{Lösung versteckt|1=Du solltest nun den Punkt E (11/10) gefunden haben.|2=Tipp zu f) und g)|3=Tipp 1 verbergen}} | |||
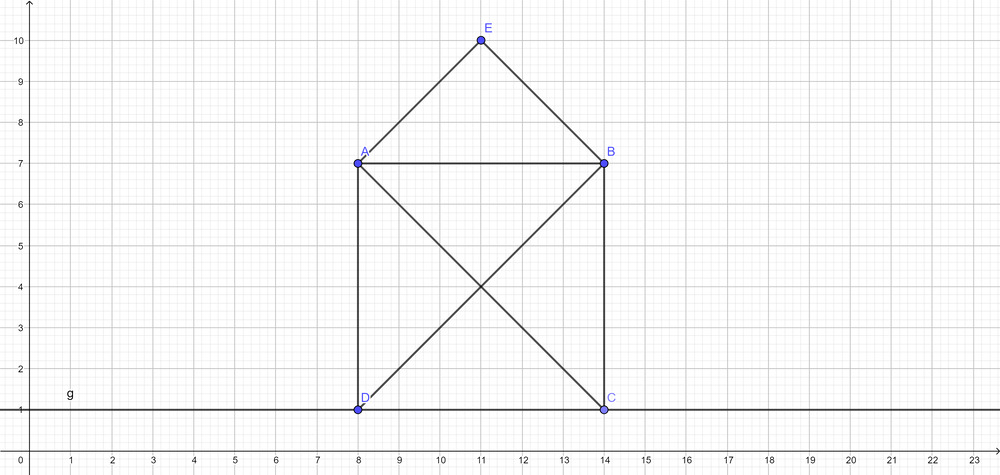
{{Lösung versteckt|1=So sollte deine Zeichnung nach i) aussehen:[[Datei:HausvomNikolaus.png|1000px]]|2=Lösung j) |3=Lösung verbergen}} | |||
| | [[Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Geometrische Figuren und Winkel/Eigenschaften von Punkt- und Spiegelsymmetrie|Nächstes Kapitel]] | ||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Kleine_Lernstandserhebung_zur_Doppeljahrgangsstufe_5/6}} | |||
Aktuelle Version vom 9. Juni 2024, 21:00 Uhr
Geraden, Strecken, Parallelen und Senkrechten
Geraden und Strecken
Senkrechten und Parallelen
Zur Erinnerung:
Die kürzeste Verbindung zwischen einem Punkt und einer Gerade ist eine Senkrechte zur Gerade g.
Du solltest nun den Punkt E (11/10) gefunden haben.