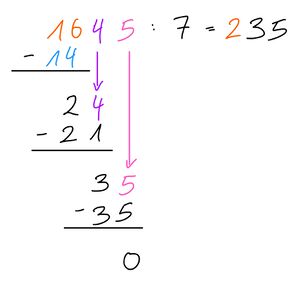Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Natürliche Zahlen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (89 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
In diesem Lernpfadkapitel widmen wir uns den natürlichen Zahlen. | In diesem Lernpfadkapitel widmen wir uns den natürlichen Zahlen. | ||
In diesem Kapitel wiederholst du | In diesem Kapitel wiederholst du ... | ||
* ... schriftliches | * ... schriftliches Addieren und Subtrahieren natürlicher Zahlen | ||
* ... Fachbegriffe und Rechengesetze für die Addition und Subtraktion | * ... Fachbegriffe und Rechengesetze für die Addition und Subtraktion | ||
* ... schriftliches | * ... schriftliches Multiplizieren und Dividieren natürlicher Zahlen | ||
* ... Fachbegriffe und Rechengesetze für die Multiplikation und Division | * ... Fachbegriffe und Rechengesetze für die Multiplikation und Division | ||
| Zeile 22: | Zeile 22: | ||
== | == Addieren und Subtrahieren von natürlichen Zahlen == | ||
===Fachbegriffe und Rechengesetze=== | ===Fachbegriffe und Rechengesetze=== | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz zu Fachbegriffen|'''Addition''' | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz zu Fachbegriffen|'''Addition''' | ||
| Zeile 53: | Zeile 45: | ||
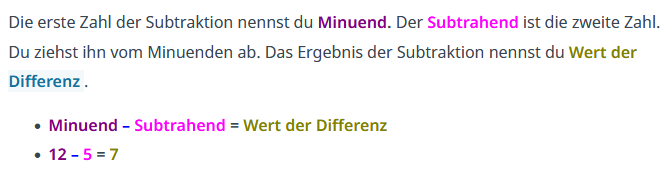
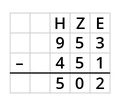
[[Datei:Subtraktio.png|links|1800px|mini]]|Merksatz | [[Datei:Subtraktio.png|links|1800px|mini]]|Merksatz | ||
| Farbe = {{Farbe|grün|dunkel}} | | Farbe = {{Farbe|grün|dunkel}} | ||
}} | }}{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 1: Fachbegriffe zur Addition und Subtraktion| | ||
'''Aufgabenstellung:''' Gib an, welches Rechengesetz dargestellt wird. Nutze dafür die Buchstaben im unteren Kasten, um die Lücken auszufüllen | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe | {{LearningApp|width=100%|height=500px|app=14302180}}|Arbeitsmethode | ||
| Farbe = #CD2990 | | Farbe = #CD2990 | ||
}} | }}{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Vertauschungsgesetz (Kommutativgesetz)|Das '''Vertauschungsgesetz (Kommutativgesetz)''' besagt: Beim Addieren kannst du die Summanden vertauschen. Das Ergebnis bleibt gleich. '''Beispiel'''<nowiki>: 83 + 92 =92 + 83</nowiki> | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Vertauschungsgesetz (Kommutativgesetz)|Das '''Vertauschungsgesetz (Kommutativgesetz)''' besagt: Beim Addieren kannst du die Summanden vertauschen. Das Ergebnis bleibt gleich. '''Beispiel'''<nowiki>: 83 + 92 =92 + 83</nowiki> | |||
| Zeile 100: | Zeile 89: | ||
Also ist (123 - 73) - 27 '''nicht '''das gleiche wie 123 - (73 - 27). | Also ist (123 - 73) - 27 '''nicht '''das gleiche wie 123 - (73 - 27). | ||
Beim '''''Subtrahieren '''''kannst du '''nicht '''beliebig Klammern setzen. Das Setzen von Klammern bei der Subtraktion führt zu unterschiedlichen | Beim '''''Subtrahieren '''''kannst du '''nicht '''beliebig Klammern setzen. Das Setzen von Klammern bei der Subtraktion führt zu unterschiedlichen Ergebnissen.|Merksatz | ||
| Farbe = {{Farbe|grün|dunkel}} | | Farbe = {{Farbe|grün|dunkel}} | ||
}}{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 2: Die Rechengesetze|<ggb_applet id="nwufy9pt" width="1000" height="600"/>|Arbeitsmethode | |||
| Farbe = #CD2990 | |||
}} | }} | ||
| Zeile 107: | Zeile 98: | ||
===Schriftliche Addition von natürlichen Zahlen=== | |||
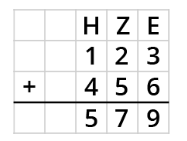
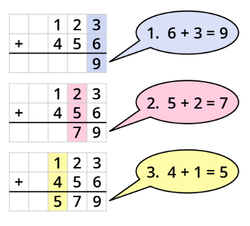
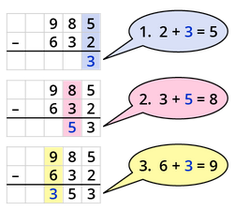
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz zur schriftlichen Addition|Die '''schriftliche Addition''' hilft dir, größere und mehrere Zahlen zu addieren. | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz zur schriftlichen Addition|Die '''schriftliche Addition''' hilft dir, größere und mehrere Zahlen zu addieren. | ||
| Zeile 162: | Zeile 145: | ||
| Farbe = {{Farbe|grün|dunkel}} | | Farbe = {{Farbe|grün|dunkel}} | ||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 3: Schriftliches Addieren mit großen Zahlen|{{LearningApp|width=100%|height=500px|app=299957}}|Arbeitsmethode | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe | | Farbe = #F19E4F | ||
| Farbe = | |||
}} | }} | ||
===Schriftliche Subtraktion von natürlichen Zahlen=== | |||
| Zeile 220: | Zeile 201: | ||
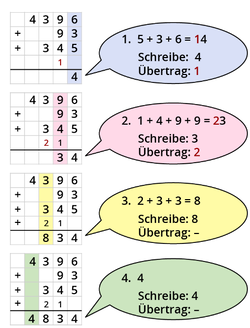
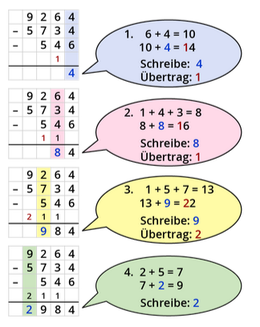
[[Datei:Subtraktion mit Übertrag.png|mini|links|328x328px]]|Merksatz | [[Datei:Subtraktion mit Übertrag.png|mini|links|328x328px]]|Merksatz | ||
| Farbe = {{Farbe|grün|dunkel}} | | Farbe = {{Farbe|grün|dunkel}} | ||
}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] [[Datei:Grundlagen-bearbeiten.png|30px|middle]] (*) Aufgabe 4: Schriftliches Subtrahieren|Schaue für eine weiterführende Aufgabenstellung dein Arbeitsblatt an. | |||
{{LearningApp|width=100%|height=650px|app=36049920}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | }} | ||
| Zeile 254: | Zeile 241: | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] [[Datei:Grundlagen-bearbeiten.png|30px|middle]] (**) Aufgabe 5: Laufen|[[Datei:Laufen.png|mini]] | |||
| | Bearbeite folgende Aufgabenstellung auf deinem Arbeitsblatt: | ||
Aysen trainiert und läuft dreimal in der Woche. Am Montag läuft sie 2 km, dazu kommen am Mittwoch 3 km, aber am Freitag kommt weniger dazu als zuvor, nur 800 m. Wie viel ist sie am Ende der Woche gelaufen? | |||
{{Lösung versteckt|1= | |||
1. Überlege zuerst: Welche Einheiten (z.B. Meter, Kilometer) kommen in der Aufgabe vor? | |||
2. Wandel die Einheiten der Strecken in eine sinnvolle und gemeinsame Einheit um. D.h. notiere die einzelnen zurückgelegten Strecken von Aysen in Metern, Kilometern... | |||
3. Jetzt kannst du alle Werte ganz einfach miteinander addieren. | |||
4. Gib das Ergebnis in Metern, also m, an. | |||
|2=Hinweis|3=Hinweis verstecken}}|Arbeitsmethode | |||
| Farbe = #CD2990 | |||
}} | |||
|2=Hinweis|3=Hinweis verstecken}} | |||
{{Lösung versteckt|1=Rechnung: | {{Lösung versteckt|1=Rechnung: | ||
2 km + 3 km + 800 m | 2 km + 3 km + 800 m | ||
= 2000 m + 3000 m + 800 m | = 2000 m + 3000 m + 800 m | ||
= 5800 m | = 5800 m | ||
Aysen ist insgesamt 5800 m gelaufen.|2=Lösung|3=Lösung verstecken | Aysen ist am Ende der Woche insgesamt 5800 m, also 5,8 km gelaufen. | ||
|2=Lösung|3=Lösung verstecken}} | |||
}} | |||
| Zeile 284: | Zeile 271: | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (***) Aufgabe | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (***) Aufgabe 6: Knobelaufgabe|{{LearningApp|width=100%|height=500px|app=3920933}}|Arbeitsmethode | ||
}} | }} | ||
== | ==Multiplizieren und Dividieren von natürlichen Zahlen== | ||
{{Box|(*) Aufgabe 1: Multiplikation Pferderennen|{{LearningApp|width=100%|height=500px|app=3232868}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||
{{Box|(*) Aufgabe 2: Division Zuordnen|{{LearningApp|width=100%|height=500px|app=18092699}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||
===Fachbegriffe und Rechengesetze=== | |||
{{Box| | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz zu den Fachbegriffen der Multiplikation und Division | ||
| Farbe = {{Farbe|grün|dunkel}}|'''Multiplizieren'''<nowiki> oder "mal rechnen" bedeutet, dass du eine Zahl mehrmals addierst. Zum Beispiel, wenn du 3•4 rechnest, bedeutet das, dass du die Zahl 3 viermal addierst. Also: 3 + 3 + 3 + 3 = 12. Das ist das Ergebnis von 3•4. Das </nowiki>'''Produkt''' ist das Ergebnis einer Multiplikation und das '''Vielfache''' ist das Ergebnis der Multiplikation einer Zahl mit einer anderen ganzen Zahl. | |||
[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] | |||
[[Datei:Screenshot 2024-05-10 105837.jpg|zentriert|mini|539x539px]] | [[Datei:Screenshot 2024-05-10 105837.jpg|zentriert|mini|539x539px]] | ||
'''Division'''<nowiki> oder "geteilt durch rechnen" bedeutet, dass du etwas in gleich große Teile aufteilst. Stell dir vor, du hast 12 Gummibärchen und möchtest sie auf 3 Freunde aufteilen. Du würdest 12 durch 3 teilen, um herauszufinden, wie viele Gummibärchen jeder Freund bekommt. In diesem Fall würden alle 3 Freunde Gummibärchen bekommen, weil 12 : 3 = 4. Das ist die Division! Es hilft uns, Dinge fair aufzuteilen. Der </nowiki>'''Divisor''' ist die Zahl, durch die du teilst und der '''Quotient''' ist das Ergebnis, wenn du Zahlen miteinander teilst. '''<u>Achtung:</u>''' Du darfst nicht durch Null teilen! | |||
[[Datei:Screenshot 2024-05-10 110117.jpg|zentriert|mini|550x550px]]|Merksatz | |||
}} | |||
{{Box|(*) Aufgabe 3: Fachbegriffe zur Multiplikation und Division|{{LearningApp|width=100%|height=500px|app=8466414}}|Arbeitsmethode | {{Box|(*) Aufgabe 3: Fachbegriffe zur Multiplikation und Division|{{LearningApp|width=100%|height=500px|app=8466414}}|Arbeitsmethode | ||
| Farbe = {{Farbe|orange}} | |||
}} | }} | ||
{{Box|(**) Aufgabe 4: | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 4: Vorteilhaftes Rechnen|Rechne vorteilhaft, indem du das Vertauschungsgesetz anwendest und notiere deine Ergebnisse im Heft: | |||
<math>4\cdot9\cdot5=</math> | |||
<math>15\cdot7\cdot2=</math> | |||
<math>2\cdot7\cdot4=</math> | |||
<math>5\cdot7\cdot5=</math> | |||
{{Lösung versteckt|1=Rechnungen: | |||
<math>4\cdot9\cdot5=4\cdot5\cdot9=20\cdot9=180</math> | |||
<math>15\cdot7\cdot2=15\cdot2\cdot7=30\cdot7=210</math> | |||
<math>2\cdot7\cdot4=2\cdot4\cdot7=8\cdot7=56</math> | |||
<math>5\cdot7\cdot5=5\cdot5\cdot7=25\cdot7=175</math>|2=Lösung|3=Lösung verstecken}}|Arbeitsmethode | |||
| Farbe = #CD2990 | |||
}} | }} | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Vertauschungsgesetz (Kommutativgesetz)|Das '''Vertauschungsgesetz (Kommutativgesetz)''' besagt: Beim Multiplizieren kannst du die Faktoren vertauschen. Das Ergebnis bleibt gleich. '''Beispiel''': <math>7\cdot8=8\cdot7</math> | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Vertauschungsgesetz (Kommutativgesetz)|Das '''Vertauschungsgesetz (Kommutativgesetz)''' besagt: Beim Multiplizieren kannst du die Faktoren vertauschen. Das Ergebnis bleibt gleich. '''Beispiel''': | |||
| Zeile 314: | Zeile 330: | ||
'''Beispiel''': | '''Beispiel''': | ||
< | <math>1\div2=0,5\neq2=2\div1</math> | ||
Also ist | Also ist <math>1\div2=0,5</math> '''nicht '''das gleiche wie <math>2\div1=2</math>. | ||
Beim ''''' | Beim '''''Dividieren '''''kannst du '''Dividend''' und '''Divisor''' '''nicht''' vertauschen. Das Vertauschen von Dividend und Divisor führt nicht zum richtigen Ergebniss.|Merksatz | ||
| Farbe = {{Farbe|grün|dunkel}} | | Farbe = {{Farbe|grün|dunkel}} | ||
}} | }} | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Verbindungsgesetz (Assoziativgesetz)|Das '''Verbindungsgesetz (Assoziativgesetz)''' besagt: Beim | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Verbindungsgesetz (Assoziativgesetz)|Das '''Verbindungsgesetz (Assoziativgesetz)''' besagt: Beim Multiplizieren kannst du beliebig Klammern setzen oder weglassen. Das Ergebnis bleibt gleich. (Hinweis: Du rechnest zuerst die Klammer wegen Klammer vor Punkt vor Strich aus). | ||
'''Beispiel''': | '''Beispiel''': | ||
< | <math>6\cdot5\cdot8=240</math> | ||
<math>(6\cdot5)\cdot8=30\cdot8=240</math> | |||
< | <math>6\cdot(5\cdot8)=6\cdot40=240</math> | ||
'''''Vorsicht bei der | '''''Vorsicht bei der Division''''' | ||
Untersuche das Setzen von Klammern bei der | Untersuche das Setzen von Klammern bei der Division. | ||
'''Beispiel''': | '''Beispiel''': | ||
< | <math>(50\div10)\div5=5\div5=1</math> | ||
< | <math>50\div(10\div5)=50\div2=25</math> | ||
Also ist ( | Also ist <math>(50\div10)\div5</math> '''nicht '''das gleiche wie <math>50\div(10\div5)</math>. | ||
Beim ''''' | Beim '''''Dividieren '''''kannst du '''nicht '''beliebig Klammern setzen. Das Setzen von Klammern bei der Division führt zu unterschiedlichen Ergebnisse.|Merksatz | ||
| Farbe = {{Farbe|grün|dunkel}} | | Farbe = {{Farbe|grün|dunkel}} | ||
}} | }} | ||
===Schriftliche Multiplikation von natürlichen Zahlen=== | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz schriftliches Multiplizieren|Für schriftliches Multiplizieren werden wir unsere Faktoren in Einer, Zehner und Hunderter (ggf. auch Tausender und höher, falls die Aufgabe dies verlangt) zerlegen. Die schriftliche Multiplikation basiert dann darauf, die einzelnen Ziffern zu multiplizieren und die Ergebnisse schließlich zu addieren. | |||
Wichtig: | |||
1) Wir rechnen von hinten nach vorne | |||
2) Beginne mit der rechten Ziffer der hinteren Zahl (der Einerstelle) und multipliziere sie mit jeder Ziffer der vorderen Zahl | |||
[[Datei:Schriftliches Multiplizieren.jpg|mini|links]]|Arbeitsmethode | |||
| Farbe = {{Farbe|grün|dunkel}} | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]](*) Aufgabe | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]](***) Aufgabe 5: Schriftliches Multiplizieren mit großen Zahlen|Multipliziere schriftlich mithilfe der App. <ggb_applet id="wes2kexr" width="1000" height="800"/>|Arbeitsmethode | ||
{{ | }} | ||
===Schriftliche Division von natürlichen Zahlen=== | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px|links]] Merksatz schriftliches Dividieren|Vorgehen: | |||
1)Du teilst die Ziffer der linken Zahl durch die rechte Zahl (Divisor ) und schreibst das Ergebnis hinter das Gleichheitszeichen. | |||
2) Du multiplizierst das Teilergebnis mit dem Divisor und schreibst es mit Minus unter linke Zahl. | |||
3) Du subtrahierst (Minus-Rechnen) | |||
4) Du holst die weiteren Ziffern "herunter" und wiederholst die Schritte | |||
[[Datei:Schriftliches Dividieren.jpg|mini|links]]|Arbeitsmethode | |||
| Farbe = {{Farbe|grün|dunkel}} | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]](**) Aufgabe | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]](**) Aufgabe 6: Schriftliches Dividieren mit großen Zahlen|Dividiere schriftlich mithilfe der App. | ||
{{LearningApp|width=100%|height=500px|app=14358230}}|Arbeitsmethode | {{LearningApp|width=100%|height=500px|app=14358230}}|Arbeitsmethode | ||
| Farbe = #CD2990 | |||
}} | |||
===Gemischte Aufgaben (Multiplikation, Division, Fachbegriffe)=== | |||
<big>''' Hinweis: Verfahren bei Textaufgaben'''</big> | |||
Suche bei Anwendungsaufgaben nach '''Signalwörtern'''. Übersetze den Text in eine Rechnung, rechne aus und schreibe einen Antwortsatz in dein Heft. | |||
{{Lösung versteckt|1= | |||
Diese Signalwörter sagen dir, dass du '''multiplizierst''': | |||
* ...mal so viel | |||
* das ...-fache | |||
* multiplizieren | |||
* verdoppeln | |||
* vervielfachen | |||
* je | |||
Diese Signalwörter sagen dir, dass du '''dividierst''': | |||
* aufteilen | |||
* halbieren | |||
* austeilen | |||
* durch | |||
* dividieren | |||
|2=Signalwörter|3=Signalwörter verstecken}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] [[Datei:Grundlagen-bearbeiten.png|30px|middle]] (**) Aufgabe 7: Erkennen von Signalwörtern der Multiplikation und Division|Schau dir dein Arbeitsblatt für die weiterführende Aufgabe an. | |||
{{LearningApp|width=100%|height=500px|app=27563340}}|Arbeitsmethode | |||
| Farbe = #CD2990 | |||
}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] [[Datei:Grundlagen-bearbeiten.png|30px|middle]] (**) Aufgabe 8: Ein Ausflug zum Möhnesee|[[Datei:Entre el mar y el cielo.JPG|mini]] | |||
Bearbeite folgende Aufgabenstellung auf deinem Arbeitsblatt: | |||
Tom, Karl, Tina, Cleo, Max, Sophia und Sarah wollen sich für einen Ausflug zum Möhnesee im Sauerland ein Schlauchboot kaufen. Für das Schlauchboot müssen sie zusammen 371€ bezahlen. Den Preis möchten die Freunde untereinander aufteilen. Wie viel muss jede bzw. jeder zahlen? | |||
{{Lösung versteckt|1= Schaue nochmal bei den Signalwörtern nach, auf welche Grundrechenart das Wort "aufteilen" hindeutet. | |||
|2=Hinweis|3=Hinweis verstecken}} | |||
{{Lösung versteckt|1=Rechnung: <math>371\div7=53</math> | |||
Jede bzw. jeder muss 53€ bezahlen.|2=Lösung|3=Lösung verstecken}}|Arbeitsmethode | |||
| Farbe = #CD2990 | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (***) Aufgabe 9: Wer wird Multiplikations- und Divisionsmeister?|{{LearningApp|width=100%|height=500px|app=paht8ugcn24}}|Arbeitsmethode | |||
}} | |||
<big> | |||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Kleine_Lernstandserhebung_zur_Doppeljahrgangsstufe_5/6}} | |||
<big> | |||
Aktuelle Version vom 10. Juni 2024, 08:37 Uhr
Addieren und Subtrahieren von natürlichen Zahlen
Fachbegriffe und Rechengesetze
Schriftliche Addition von natürlichen Zahlen
Schriftliche Subtraktion von natürlichen Zahlen
Gemischte Aufgaben (Addition, Subtraktion, Fachbegriffe)
Hinweis: Verfahren bei Textaufgaben
Suche bei Anwendungsaufgaben nach Signalwörtern. Übersetze den Text in eine Rechnung, rechne aus und schreibe einen Antwortsatz in dein Heft.
Diese Signalwörter sagen dir, dass du subtrahierst:
- vermindert
- weniger
- Abnahme
- wegnehmen
- verringern
- abziehen
Diese Signalwörter sagen dir, dass du addierst:
- vermehrt
- mehr
- Zuwachs
- dazu
- hinzufügen
Rechnung: 2 km + 3 km + 800 m = 2000 m + 3000 m + 800 m = 5800 m
Aysen ist am Ende der Woche insgesamt 5800 m, also 5,8 km gelaufen.
Multiplizieren und Dividieren von natürlichen Zahlen
Fachbegriffe und Rechengesetze
Schriftliche Multiplikation von natürlichen Zahlen
Schriftliche Division von natürlichen Zahlen
Gemischte Aufgaben (Multiplikation, Division, Fachbegriffe)
Hinweis: Verfahren bei Textaufgaben
Suche bei Anwendungsaufgaben nach Signalwörtern. Übersetze den Text in eine Rechnung, rechne aus und schreibe einen Antwortsatz in dein Heft.
Diese Signalwörter sagen dir, dass du multiplizierst:
- ...mal so viel
- das ...-fache
- multiplizieren
- verdoppeln
- vervielfachen
- je
Diese Signalwörter sagen dir, dass du dividierst:
- aufteilen
- halbieren
- austeilen
- durch
- dividieren