Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Flächen und Körper/Flächeninhalt: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (25 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Flächeninhalt == | == Flächeninhalt == | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 7: Flächeninhalt grafisch herleiten und berechnen|Mit dem folgenden Applet kannst du noch einmal überlegen, wie man den Flächeninhalt einer Fläche berechnet. Wenn du die richtige Formel gefunden hast, schreibe sie bitte in das Feld auf dem Arbeitsblatt für "Flächen und Körper". Falls du nicht auf die Lösung kommen solltest, kannst du sie weiter unten nachgucken. | |||
<ggb_applet id="zrvndw67" width="800" height="680" border="88888"></ggb_applet>|Arbeitsmethode|Farbe = {{Farbe|Orange}} | |||
}} | |||
{{Box| | _________________________________________________________________________________________________________________________________________________________________________________________________________________ | ||
{{Box|[[Datei:Info black.png|links|rahmenlos|30x30px]] Info|Hier sind noch einmal die beiden Formeln für Rechtecke und Quadrate zur Berechnung des Flächeninhaltes dargestellt| Info|Farbe = {{Farbe|grau}} | |||
}} | |||
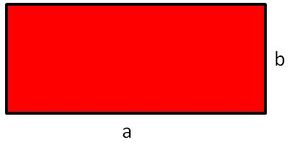
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merke dir für den Flächeninhalt des Rechtecks|2=[[Datei:Flächeninhalt Rechteck Bild.jpg|rechts|rahmenlos]]<span style ="color:red">IN</span>nen dr<span style="color:red">IN</span>!<br> | |||
'''<big><u>Rechteck</u></big>'''<br> | '''<big><u>Rechteck</u></big>'''<br> | ||
<big>A = Länge | <big><math>\begin{align} | ||
& | A &= Länge \cdot Breite\\ | ||
&= a \cdot b | |||
\end{align}</math></big>|3= Merksatz | |||
|Farbe = {{Farbe|grün}}}} | |||
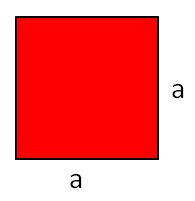
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merke dir für den Flächeninhalt des Quadrates | |||
| 2 = '''<big><u>Quadrat</u></big>'''<br> | |||
[[Datei:Flächeninhalt Quadrat.jpg|rechts|rahmenlos]] | |||
<big><math>\begin{align} | |||
A &= Länge \cdot Breite\\ | |||
&= a \cdot a\\ | |||
&= a^2 | |||
\end{align}</math></big> | |||
| 3 = Merksatz | |||
| Farbe = {{Farbe|grün}} | |||
}} | |||
====Aufgaben zum Üben==== | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 8: Flächeninhalte erkennen|In der folgenden Aufgabe sollst du entscheiden, ob ein Flächeninhalt berechnet wird oder nicht. Kreuze dazu bei 5-6 Aufgaben die richtige Antwort an. | |||
<ggb_applet id="ajdy7jqs" width="800" height="580" border="88888" />|Arbeitsmethode | |||
| Farbe = #CD2990 | |||
}} | |||
{{Box| | _________________________________________________________________________________________________________________________________________________________________________________________________________________ | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 9: Flächeninhalte berechnen|Berechne im Kopf den Flächeninhalt der Fläche und wähle die richtige Lösung! In dem Applet findest du links oben ein kleine Glühbirne. Tippst du darauf, bekommst du eine kleine Hilfe! | |||
[[Datei: | <iframe src="https://learningapps.org/watch?app=17078895" style="border:0px;width:100%;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>|Arbeitsmethode | ||
< | | Farbe = #CD2990 | ||
}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Überprüfungsaufgabe:|Benedikt möchte zwei Wände in seinem Zimmer neu streichen. Das Zimmer hat eine Deckenhöhe von 2m und die beiden Wände sind 4m und 2,5m lang. Wie viel Quadratmeter muss Benedikt insgesamt streichen?|Arbeitsmethode | |||
| Farbe = #CD2990 | |||
}} | |||
{{Lösung versteckt|Insgesamt muss Benedikt <math>2m \cdot 4m + 2m \cdot 2,5m = 8m^2 + 5m^2 = 13m^2</math> streichen|Lösung anzeigen|Lösung verbergen}} | |||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] Nachdem du diese Seite bearbeitet hast, bearbeite auf dem ausgeteilten Arbeitsblatt den obigen Kasten nun vollständig. Treffe neben den bereits getätigten Aussagen zum Umfang nun auch Aussagen zum Flächeninhalt | |||
_________________________________________________________________________________________________________________________________________________________________________________________________________________ | _________________________________________________________________________________________________________________________________________________________________________________________________________________ | ||
[[Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Flächen und Körper|Klicke hier um zur '''Ausgangsseite: Flächen und Körper''' zurückzukehren]] | [[Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Flächen und Körper|Klicke hier um zur '''Ausgangsseite: Flächen und Körper''' zurückzukehren]] | ||
Aktuelle Version vom 7. Juni 2024, 13:45 Uhr
Flächeninhalt
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Aufgaben zum Üben
_________________________________________________________________________________________________________________________________________________________________________________________________________________
![]() Nachdem du diese Seite bearbeitet hast, bearbeite auf dem ausgeteilten Arbeitsblatt den obigen Kasten nun vollständig. Treffe neben den bereits getätigten Aussagen zum Umfang nun auch Aussagen zum Flächeninhalt
Nachdem du diese Seite bearbeitet hast, bearbeite auf dem ausgeteilten Arbeitsblatt den obigen Kasten nun vollständig. Treffe neben den bereits getätigten Aussagen zum Umfang nun auch Aussagen zum Flächeninhalt
_________________________________________________________________________________________________________________________________________________________________________________________________________________ Klicke hier um zur Ausgangsseite: Flächen und Körper zurückzukehren