Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Flächen und Körper/Umfang berechnen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (65 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Umfang berechnen == | == Umfang berechnen == | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*)Aufgabe 4: Den Umfang auseinanderziehen|Wiederhole mit dem folgenden Applet noch einmal, wie man den Umfang einer Fläche berechnet. Wenn du die richtige Lösung kennst oder herausgefunden hast, trage sie bitte in das passende Feld auf dem Arbeitsblatt zum Thema "Flächen und Körper" ein. | |||
<ggb_applet id="wdgpkuca" width="800" height="580" border="888888" />|Arbeitsmethode|Farbe = {{Farbe|Orange}} | |||
}} | |||
{{Box| | _________________________________________________________________________________________________________________________________________________________________________________________________________________ | ||
{{Box|[[Datei:Info black.png|links|rahmenlos|30x30px]] Info|In den beiden folgenden Kästen sind die Formeln zur Berechnung eines Rechtecks und eines Quadrates aufgeführt. Merke dir am Besten, dass man bei jeder Fläche alle Seitenlängen der Fläche addieren muss und werfe danach einen Blick auf dein Arbeitsblatt. Die ersten Aufgaben kannst du dort jetzt schon erledigen.|Info | |||
|Farbe = {{Farbe|grau}} | |||
}} | |||
{{Box | |||
| [[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merke dir für den Umfang des Rechtecks | |||
| 2 = [[Datei:Umfang_Rechteck.jpg|rahmenlos|rechts]] Man läuft dr<span style="color:red">UM</span> her<span style="color:red">UM</span>!<br> | |||
'''<big><u>Rechteck</u></big>'''<br> | |||
<big>u = a + b + a + b<br> | |||
= 2·a + 2·b<br> | |||
= 2·(a + b)</big><br> | |||
| 3 = Merksatz | |||
|Farbe = {{Farbe|grün}} | |||
}} | |||
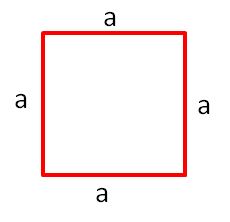
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merke dir für den Umfang des Quadrates|2=[[Datei:Umfang_Quadrat.jpg|rechts|rahmenlos]]<br> | |||
'''<big><u>Quadrat</u></big>'''<br> | |||
<big>u = a + a + a + a<br> | |||
= 4·a<br></big> | |||
<br>|3=Merksatz | |||
|Farbe = {{Farbe|grün}}}} | |||
==== Aufgaben zum Vertiefen und Rechnen ==== | |||
<ggb_applet id=" | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 5: Umfang erkennen|Kannst du schon entscheiden, ob ein Umfang berechnet wird oder nicht? Entscheide, ob ein Umfang berechnet wird oder nicht. Bearbeite dazu 4-5 Aufgaben. | ||
<ggb_applet id="nwxpd6dm" width="800" height="580" border="88888" />|Arbeitsmethode|Farbe = #CD2990 | |||
}} | |||
_________________________________________________________________________________________________________________________________________________________________________________________________________________ | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 6: Umfang berechnen|In der folgenden Aufgabe sollst du selber einmal den Umfang von verschiedenen Flächen berechnen. Falls du dabei nicht weiterkommst, gibt es unter dem Applet einen Tipp für dich. Bearbeite auch hier 4-5 Aufgaben. | |||
<ggb_applet id="ug5y6qry" width="800" height="580" border="88888" />|Arbeitsmethode|Farbe = #CD2990 | |||
}} | |||
{{Lösung versteckt|Versuche dir die Figur in dein Heft zu übertragen und dir einmal alle fehlenden Seitenlängen hinzuschreiben. Denk daran, dass die gegenüberliegenden Seiten von einem Quadrat und einem Rechteck immer gleich lang sind.|Tipp 1 anzeigen|Tipp verbergen}} | |||
{{Lösung versteckt|Der Umfang wird berechnet in dem du alle Seitenlängen addierst.|Tipp 2 anzeigen|Tipp verbergen}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Überprüfungsaufgabe: | |||
|Bauer Heinrich möchte seine rechteckige Weide einzäunen und weiß, dass zwei anei | |||
nandergrenzende Seiten 6m & 9m lang sind. Wie viel Meter Zaun sollte der Bauer kaufen, damit dieser für die ganze Weide reicht? | |||
|Arbeitsmethode|Farbe = #CD2990}} | |||
{{Lösung versteckt|Der Bauer sollte <math>6m \cdot 2 + 9m \cdot 2 = 12m + 18m = 30m</math> Zaun kaufen.|Lösung anzeigen|Lösung verbergen}} | |||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Nachdem du diese Seite bearbeitet hast, bearbeite auf dem ausgeteilten Arbeitsblatt den obigen Kasten zur Hälfte. Treffe lediglich Aussagen zum Umfang.''' | |||
_________________________________________________________________________________________________________________________________________________________________________________________________________________ | |||
[[Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Flächen und Körper/Flächeninhalt|Klicke hier um zum '''nächsten Thema: Flächeninhalte berechnen''' zu gelangen]] | |||
[[Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Flächen und Körper|Klicke hier um zur '''Ausgangsseite: Flächen und Körper''' zurückzukehren]] | |||
Aktuelle Version vom 9. Juni 2024, 21:06 Uhr
Umfang berechnen
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Aufgaben zum Vertiefen und Rechnen
_________________________________________________________________________________________________________________________________________________________________________________________________________________
![]() Nachdem du diese Seite bearbeitet hast, bearbeite auf dem ausgeteilten Arbeitsblatt den obigen Kasten zur Hälfte. Treffe lediglich Aussagen zum Umfang.
Nachdem du diese Seite bearbeitet hast, bearbeite auf dem ausgeteilten Arbeitsblatt den obigen Kasten zur Hälfte. Treffe lediglich Aussagen zum Umfang.
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Klicke hier um zum nächsten Thema: Flächeninhalte berechnen zu gelangen
Klicke hier um zur Ausgangsseite: Flächen und Körper zurückzukehren