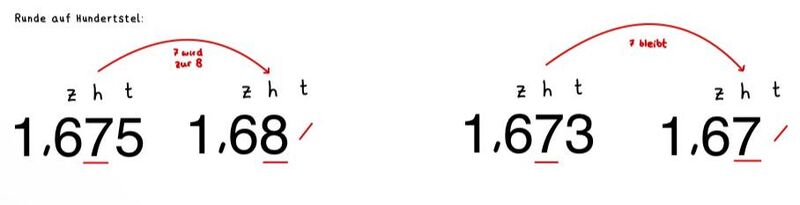Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Dezimalzahlen und Umgang mit Größen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (120 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
| 2 = In diesem Lernpfadkapitel wiederholen wir mit dir die Dezimalzahlen und den Umgang mit Größen. | | 2 = In diesem Lernpfadkapitel wiederholen wir mit dir die Dezimalzahlen und den Umgang mit Größen. | ||
In diesem Kapitel | In diesem Kapitel wecken wir zusammen deine Erinnerungen ... | ||
* | * zu den Begrifflichkeiten der Dezimalzahlen | ||
* | * zu den Darstellungsweisen einer rationalen Zahl | ||
* | * zum Runden und Rechnen mit Dezimalzahlen | ||
* | * zum Umgang mit Größen in Dezimalschreibweise | ||
Bei den Aufgaben unterscheiden wir folgende Typen: | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
| Zeile 14: | Zeile 14: | ||
* Aufgaben in '''<span style="color: #CD2990">pinker</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | * Aufgaben in '''<span style="color: #CD2990">pinker</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | ||
* Und Aufgaben mit '''<span style="color: #5E43A5">lilanem</span>''' Streifen sind '''Knobelaufgaben'''. | * Und Aufgaben mit '''<span style="color: #5E43A5">lilanem</span>''' Streifen sind '''Knobelaufgaben'''. | ||
* Bei einigen Aufgaben findest du oben links ein kleines '''Fragezeichen''' oder eine '''Glühlampe'''. Wenn du die Aufgabenstellung nochmal lesen möchtest, klicke auf das Fragezeichen. Wenn du einen Tipp brauchst, klicke auf die Glühlampe. | |||
Viel Spaß! | Viel Spaß! | ||
| 3 = Kurzinfo | | 3 = Kurzinfo | ||
| Zeile 19: | Zeile 20: | ||
==Einführung== | ==Einführung== | ||
Dezimalzahlen tauchen in unserem Alltag fast überall auf | Dezimalzahlen tauchen in unserem Alltag fast überall auf: im Supermarkt, beim Wiegen von Lebensmitteln, beim Messen deiner Körpergröße oder an der Tankstelle mit deinen Eltern. Deswegen kannst du die Dezimalzahlen und den Umgang mit Größen in diesem Lernpfad mit den wichtigsten Begriffen und Rechengesetzen wiederholen. | ||
[[Datei:Alltag_Supermarkt_2.jpg|220x220px]] [[Datei:Alltag_Wegweiser.jpg|220x220px]] [[Datei:Alltag_Tankstelle.jpg|293x293px]] [[Datei:Alltag_Wiegen.jpg|220x220px]] [[Datei:Alltag Supermarkt.jpg|220x220px]] | |||
===Erinnerst du dich noch an die Dezimalzahlen?=== | ===Erinnerst du dich noch an die Dezimalzahlen?=== | ||
| Zeile 26: | Zeile 28: | ||
'''Dezimalzahlen''' kannst du in eine erweiterte Stellenwerttafel eintragen. Dezimalzahlen sind Brüche in einer anderen Schreibweise. | '''Dezimalzahlen''' kannst du in eine erweiterte Stellenwerttafel eintragen. Dezimalzahlen sind Brüche in einer anderen Schreibweise. | ||
Dezimalzahlen kannst du als Brüche mit den Nennern 10, 100, 1000, ... schreiben und andersherum. |Merksatz | Dezimalzahlen kannst du als Brüche mit den Nennern <math>10, 100, 1000, ...</math> schreiben und andersherum. | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]]''Notiere dir den Merksatz in das zugehörige Feld auf dem Arbeitsblatt.''|Merksatz | |||
| Farbe = {{Farbe|grün}} | | Farbe = {{Farbe|grün}} | ||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 1: Vor- und Nachkommastellen einer Dezimalzahl|{{LearningApp|width=100%|height=500px|app=35466334}}|Aufgabe | ||
| Farbe = {{Farbe|orange}} | | Farbe = {{Farbe|orange}} | ||
}} | }} | ||
===Vor- und Nachkommastelle in der Stellenwerttafel=== | ===Vor- und Nachkommastelle in der Stellenwerttafel=== | ||
{{Box | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe|<ggb_applet id="kdapxmsh" width=" | | 1 = [[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 2: Dezimalzahlen in der Stellenwerttafel | ||
| 2 = Trage die Ziffern der Zahl an die richtigen Stellen der Stellenwerttafel. Übe das Verfahren mit 3 bis 5 neuen Zahlen. | |||
<ggb_applet id="kdapxmsh" width="1400" height="500" border="888888" /> | |||
| 3 = Aufgabe | |||
| Farbe = {{Farbe|orange}} | | Farbe = {{Farbe|orange}} | ||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe|<ggb_applet id="j5yeytef" width="1265" height="642" border="888888" />|Aufgabe | {{Box | ||
| 1 = [[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 3: Dezimalzahlen in der Stellenwerttafel | |||
| 2 = Schreibe die Zahl aus der Stellenwerttafel als Dezimalzahl auf. Übe das Verfahren mit 3 bis 5 neuen Zahlen. | |||
<ggb_applet id="j5yeytef" width="1265" height="642" border="888888" /> | |||
| 3 = Aufgabe | |||
| Farbe = #CD2990 | | Farbe = #CD2990 | ||
}} | }} | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: Größen|Größen sind '''Geld, Gewicht (Masse), Länge '''und '''Zeit'''. Größen bestehen aus '''Maßzahl''' und '''Einheit'''.|Merksatz | ===Umgang mit Größen=== | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: Größen|Größen sind '''Geld, Gewicht (Masse), Länge '''und '''Zeit'''. Größen bestehen aus '''Maßzahl''' und '''Einheit'''. | |||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]]''Notiere dir den Merksatz in das zugehörige Feld auf dem Arbeitsblatt.''|Merksatz | |||
| Farbe = {{Farbe|grün}} | | Farbe = {{Farbe|grün}} | ||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 4: Größen im Alltag|{{LearningApp|width=100%|height=500px|app=35467673}}|Aufgabe | |||
| Farbe = {{Farbe|orange}} | | Farbe = {{Farbe|orange}} | ||
}} | }} | ||
{{Box | |||
| 1 = [[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: Größeneinheiten | |||
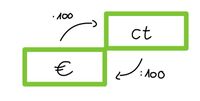
| 2 = '''Geld''': Euro (<math>€</math>), Cent (<math>ct</math>) | |||
[[Datei:Umwandeln von Geldeinheiten.jpg|links|200px|rahmenlos]] | |||
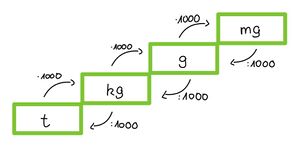
'''Gewicht''': Tonne (<math>t</math>), Kilogramm (<math>kg</math>), Gramm (<math>g</math>), Milligramm (<math>mg</math>) | |||
[[Datei:Umwandeln von Gewicht.jpg|rahmenlos]] | |||
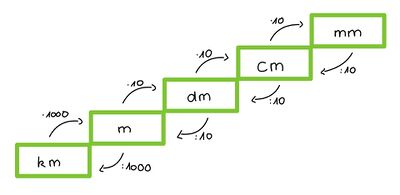
'''Länge''': Kilometer (<math>km</math>), Meter (<math>m</math>), Dezimeter (<math>dm</math>), Zentimeter (<math>cm</math>), Millimeter (<math>mm</math>) | |||
[[Datei:Umwandeln von Länge.jpg|400px|rahmenlos]] | |||
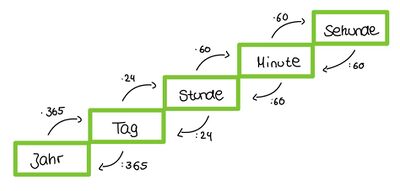
'''Zeit''': Jahre, Tage (<math>d</math>), Stunden (<math>h</math>), Minuten (<math>min</math>), Sekunden (<math>s</math>) | |||
[[Datei:Umwandeln von Zeit.jpg|400px|rahmenlos]] | |||
| 3 = Merksatz | |||
| Farbe = {{Farbe|grün}} | | Farbe = {{Farbe|grün}} | ||
}} | }} | ||
| Zeile 81: | Zeile 96: | ||
==Dezimalzahlen in der Welt der Größen== | ==Dezimalzahlen in der Welt der Größen== | ||
=== Drei Darstellungszahlen einer rationalen Zahl === | ===Drei Darstellungszahlen einer rationalen Zahl=== | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: Dezimalzahlen, Brüche, Prozentzahlen | {{Box | ||
| Eine Dezimalzahl ist eine Zahl mit einem Komma. Sie lässt sich | | 1 = [[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: Dezimalzahlen, Brüche, Prozentzahlen | ||
| 2 = Eine Dezimalzahl ist eine Zahl mit einem Komma. Sie lässt sich jedoch auch als Bruch oder Prozentzahl darstellen. | |||
Beispiel: | |||
Dezimalzahl: <math>0,5</math> | |||
und Bruch: <math>\frac{1}{2}</math> | |||
und Prozentzahl: <math>50 \%</math> | |||
<math>\Rightarrow 0,5 = \frac{1}{2} = 50\%</math> | |||
'''Wechsel vom Bruch zur Dezimalzahl:''' | '''Wechsel vom Bruch zur Dezimalzahl:''' | ||
Kürzere oder erweitere den Nenner der Zahl auf 10, 100, 1000 ... (Hinweis: bei der Dezimalzahl denkst du dir, dass sie eine 1 im Nenner hat). Wechsele dann in die Dezimalschreibweise. | |||
Beispiel: 4 | Kürzere oder erweitere den Nenner der Zahl auf <math>10, 100, 1000, ...</math> (Hinweis: bei der Dezimalzahl denkst du dir, dass sie eine 1 im Nenner hat). Wechsele dann in die Dezimalschreibweise. | ||
Beispiel: <math>\frac{4}{5} = \frac{8}{10} = 0,8</math> | |||
'''Wechsel von der Dezimalzahl zum Bruch:''' | '''Wechsel von der Dezimalzahl zum Bruch:''' | ||
Erweitere den Nenner der Dezimalzahl (du denkst dir, dass die Dezimalzahl zunächst den Nenner 1 hat) auf 10, 100, 1000 | |||
Beispiel: 2,67 (= 2,67 | Erweitere den Nenner der Dezimalzahl (du denkst dir, dass die Dezimalzahl zunächst den Nenner 1 hat) auf <math>10, 100, 1000, ...</math> je nachdem, wie viele Nachkommastellen du hast. Das heißt, wenn du drei Nachkommastellen hast, erweiterst du auf den Nenner <math>1000</math>. | ||
Wenn möglich, kannst du den Bruch dann noch kürzen. | |||
Beispiel: <math>2,67</math> <math> (= \frac{2,67}{1}) = \frac{267}{100}</math> | |||
Wenn möglich, kannst du den Bruch dann noch kürzen. | |||
'''Wechsel von Dezimalzahlen oder Brüchen zu Prozentzahlen:''' | '''Wechsel von Dezimalzahlen oder Brüchen zu Prozentzahlen:''' | ||
Das Prozent-Zeichen % steht für Hundertstel (1 von 100). | |||
Beispiele: 1 | Das Prozent-Zeichen <math>\%</math> steht für Hundertstel (1 von 100). Das heißt, du kannst einen Bruch, der als Nenner die <math>100</math> hat auch als Prozentangabe schreiben. | ||
Beispiele: | |||
<math>\frac{1}{100} = 0,01 = 1\%</math> | |||
<math>\frac{3}{10} = \frac{30}{100} = 0,3 = 30\%</math> | |||
<math>\frac{2}{5} = \frac{40}{100} = 0,4 = 40\%</math> | |||
| 3 = Merksatz | |||
| Farbe = {{Farbe|grün}} | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 5: Wechsel der Darstellungsformen|{{LearningApp|width=100%|height=500px|app=35467586}}|Aufgabe | ||
| Farbe = {{Farbe|orange}} | | Farbe = {{Farbe|orange}} | ||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**/***) Aufgabe 6: Wechsel und Ordnung der Darstellungsformen|{{LearningApp|width=100%|height=500px|app=35468079}}|Aufgabe | ||
| Farbe = #CD2990 | | Farbe = #CD2990 | ||
}} | }} | ||
{{Box|[[Datei:Icon- | ===Das Geheimnis des Rundens von Dezimalzahlen=== | ||
< | {{Box | ||
| Farbe = | | 1 = [[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]Merksatz: Runden und Überschlagen bei Dezimalzahlen | ||
| 2 = Vor dem '''Runden''' von Dezimalzahlen muss du festlegen, wie viele Stellen nach dem Komma die gerundete Zahl haben soll. | |||
Vervollständige den Merksatz. | |||
<div class="lueckentext-quiz"> | |||
Ist die erste Ziffer, die du weglässt, 0; 1; 2; 3 oder 4, so wird '''abgerundet'''. | |||
Ist die erste Ziffer, die du weglässt, 5; 6; 7; 8 oder 9, so wird '''aufgerundet'''. | |||
</div> | |||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]]''Wenn du alle Lücken richtig ausgefüllt hast, schreibe den Merksatz auf dein Arbeitsblatt.'' | |||
| 3 = Merksatz | |||
| Farbe = {{Farbe|grün|dunkel}} | |||
}} | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]Beispiel: Runden und Überschlagen bei Dezimalzahlen|Schaue dir das Beispiel an. | |||
[[Datei:Beispiel Runden und Überschlagen bei Dezimalzahlen.jpg|links|rahmenlos|800px|Beispiel Runden und Überschlagen bei Dezimalzahlen]]|Aufgabe | |||
| Farbe = {{Farbe|gelb}} | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 7: Dezimalzahlen runden|{{LearningApp|width=100%|height=500px|app=3276966}}|Aufgabe | |||
| Farbe = #CD2990 | |||
{{Box|[[Datei:Icon- | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (***) Aufgabe 8: Runden von Dezimalzahlen|[[Datei:Grundlagen-bearbeiten.png|30px|middle]]Bearbeite diese Aufgabe auf dem Arbeitsblatt. | |||
a) Gib an, auf welche Stelle gerundet wurde: <math>0,982 \approx 0,98</math> | |||
b) Runde <math>27,943</math> auf Zehntel. | |||
c) Nenne drei Dezimalzahlen, die gerundet <math>4,75</math> ergeben. | |||
d) Gib die größte Zahl mit vier Nachkommastellen an, die auf Hundertstel gerundet <math>2,67</math> ergibt. | |||
{{Lösung versteckt|1=Es wurde auf '''Hundertstel '''gerundet. | |||
|2=Lösung a)|3=Lösung verbergen}} | |||
{{Lösung versteckt|1=<math>27,943 \approx 27,9</math> | |||
|2=Lösung b)|3=Lösung verbergen}} | |||
{{Lösung versteckt|1=Folgende Zahlen ergeben <math>4,75</math> gerundet auf Hundertstel: '''<math>4,745; 4,746; 4,747; 4,748; 4,749; 4,750; 4,751; 4,752; 4,753; 4,754</math>''' | |||
|2=Lösung c)|3=Lösung verbergen}} | |||
{{Lösung versteckt|1=Die größte Zahl mit vier Nachkommastellen, die auf Hundertstel gerundet <math>2,67</math> ergibt lautet '''<math>2,6749</math>'''. | |||
|2=Lösung d)|3=Lösung verbergen}}|Aufgabe | |||
| Farbe = #5E43A5 | |||
}} | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz | ===Rechengesetze=== | ||
Tipp: Nullen ergänzen und Fehler vermeiden!|Merksatz| Farbe = {{Farbe|grün}} | ====Addition und Subtraktion von Dezimalzahlen==== | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: Addition und Subtraktion von Dezimalzahlen|Wie bei den ganzen Zahlen addiert und subtrahiert man auch Dezimalzahlen stellenweise. Dies gilt ebenso, wenn die Anzahl der Nachkommastellen unterschiedlich ist. Damit gleiche Stellen beim schriftlichen Rechnen untereinander stehen, muss Komma unter Komma stehen. | |||
Tipp: Nullen ergänzen und Fehler vermeiden!|Merksatz | |||
| Farbe = {{Farbe|grün}} | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 9: Dezimalbrüche addieren|{{LearningApp|width=100%|height=500px|app=1388189}}|Aufgabe | ||
| Farbe = {{Farbe|orange}} | | Farbe = {{Farbe|orange}} | ||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 10: Dezimalbrüche addieren und subtrahieren|{{LearningApp|width=100%|height=500px|app=1911134}}|Aufgabe | ||
| Farbe = #CD2990 | | Farbe = #CD2990 | ||
}} | }} | ||
==== Multiplikation von Dezimalzahlen ==== | ====Multiplikation von Dezimalzahlen==== | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: Multiplikation von Dezimalzahlen|# Bestimme das Vorzeichen (<math>+</math> und <math>+ \rightarrow +</math>; <math>+</math> und <math>- \rightarrow -</math>; <math>-</math> und <math>- \rightarrow +</math>). | ||
# Bestimme das Vorzeichen (+ und + | |||
# Multipliziere zuerst, ohne auf das Komma zu achten. | # Multipliziere zuerst, ohne auf das Komma zu achten. | ||
# Verschiebe beim Ergebnis das Komma um so viele Stellen nach links wie die Summe der Nachkommastellen beider Faktoren. | # Verschiebe beim Ergebnis das Komma um so viele Stellen nach links wie die Summe der Nachkommastellen beider Faktoren. | ||
Tipp: Runde zunächst die Dezimalzahlen und überschlage das Ergebnis im Kopf, so vermeidest du Fehler in der Größenordnung des Ergebnisses!|Merksatz| Farbe = {{Farbe|grün}} | Tipp: Runde zunächst die Dezimalzahlen und überschlage das Ergebnis im Kopf, so vermeidest du Fehler in der Größenordnung des Ergebnisses!|Merksatz | ||
| Farbe = {{Farbe|grün}} | |||
}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 11: Rechnen im Kopf|Rechne folgende Aufgaben im Kopf. | |||
a) <math>0,4 \cdot 0,6</math> | |||
b) <math>0,5 \cdot 0,01</math> | |||
c) <math>0,72 \div 0,08</math> | |||
{{Lösung versteckt|1= a) <math>0,24</math> | |||
b) <math>0,005</math> | |||
c) <math>9</math> | |||
|2=Lösung |3=Lösung verbergen}}|Aufgabe | |||
| Farbe = {{Farbe|orange}} | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (***) Aufgabe 12: Addition und Multiplikation von Dezimalzahlen|Max kauft <math>1,034 kg</math> Möhren und <math>0,731 kg</math> Tomaten. [[Datei:Lernpfad Mathe Didaktik.jpg|thumb|Preise für Möhren, Kartoffeln und Tomaten|400x400px]] | ||
Wie viel muss er zahlen? Runde sinnvoll. | |||
{{Lösung versteckt|1= Für die Möhren muss Max <math>1,034 kg \cdot 0,79 €/kg = 0,82 €</math> bezahlen. | |||
Für die Tomaten muss Max <math>0,731 kg \cdot 2,99 €/kg = 2,19 €</math> bezahlen. | |||
Insgesamt muss er also <math>0,82 € + 2,19 € = 3,01 €</math> bezahlen. | |||
Info: Bei Geld ist es sinnvoll, auf zwei Nachkommastellen zu runden, weil dies den Cent-Betrag beschreibt und wir bei Geld keine kleinere Einheit als Cent haben. | |||
|2=Lösung |3=Lösung verbergen}}|Aufgabe | |||
| Farbe = #5E43A5 | | Farbe = #5E43A5 | ||
}} | }} | ||
=== Verhältnisse von Größen === | ===Verhältnisse von Größen=== | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz | {{Box | ||
* Gewicht: ... mg < g < kg < t ..., wobei die Einheiten sich jeweils um den Faktor 1000 unterscheiden | | 1 = [[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz: Größen und Verhältnisse von Größen | ||
* Länge: mm < cm < dm < m < km ..., wobei sich die Einheiten von mm bis m jeweils um den Faktor 10 unterscheiden und m und km um den Faktor 1000 | | 2 = Du kennst bereits die verschiedenen Größen Gewicht, Länge, Geld und Zeit. Ein Vergleich kann immer nur innerhalb einer Größe stattfinden, d.h. du kannst nicht <math>3 kg</math> mit <math>50 m</math> vergleichen. Die Größen werden durch verschiedene Einheiten angegeben, die du beim Vergleich beachten musst. Erinnerung: | ||
* Geld: ct < €, wobei 100ct = 1€ | * Gewicht: <math>... mg < g < kg < t ...</math>, wobei die Einheiten sich jeweils um den Faktor <math>1000</math> unterscheiden | ||
* Zeit: ... s < min < h < d (Tage) < Jahre, wobei 60 s = 1 min, 60 min = 1 h, 24 h = 1 d und 365 d = 1 Jahr | * Länge: <math>mm < cm < dm < m < km ...</math>, wobei sich die Einheiten von <math>mm</math> bis <math>m</math> jeweils um den Faktor <math>10</math> unterscheiden und <math>m</math> und <math>km</math> um den Faktor <math>1000</math> | ||
Tipp: Wenn du zwei Größen vergleichen willst, z.B. 1500 g und 2 kg, so bringe alle Größen auf dieselbe Einheit und vergleiche dann: 2 kg = 2000 g | * Geld: <math>ct < €</math>, wobei <math>100ct = 1€</math> | ||
* Zeit: ... <math>s < min < h < d (Tage) < Jahre</math>, wobei <math>60 s = 1 min</math>, <math>60 min = 1 h</math>, <math>24 h = 1 d</math> und <math>365 d = 1 Jahr</math> | |||
Tipp: Wenn du zwei Größen vergleichen willst, z.B. <math>1500 g</math> und <math>2 kg</math>, so bringe alle Größen auf dieselbe Einheit und vergleiche dann: <math>2 kg = 2000 g > 1500 g < 2000 g = 2 kg</math> | |||
| 3 = Merksatz | |||
| Farbe = {{Farbe|grün}} | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 13: Objekte nach Gewicht sortieren|{{LearningApp|width=100%|height=500px|app=35498085}}|Aufgabe | ||
| Farbe = | | Farbe = {{Farbe|orange}} | ||
}} | }} | ||
{{Box|[[Datei:Icon- | |||
| Farbe = | [[Datei:Madita_Abeln.png|rechts|rahmenlos]] | ||
{{Box | |||
| 1 = [[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]Merksatz: Dezimalschreibweise von Größen | |||
| 2 = Vervollständige den Merksatz. | |||
<div class="lueckentext-quiz"> | |||
Bei der Dezimalschreibweise von Größen entspricht der Wechsel zu einer '''größeren '''Maßeinheit einer Kommaverschiebung nach links. Der Wechsel zu einer '''kleineren '''Maßeinheit entspricht einer Kommaverschiebung nach rechts. Das Komma wird um eine, um zwei, um drei Stellen verschoben, wenn die eine Maßeinheit das '''10fache''', das '''100fache''', das '''1000fache '''der anderen Maßeinheit ist. | |||
</div> | |||
| 3 = Merksatz | |||
| Farbe = {{Farbe|grün|dunkel}} | |||
}} | }} | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]Beispiel: Einheiten|Schreibe in der angegebenen Einheit. | |||
a) <math>2,68 m</math> (in <math>dm</math>) | |||
b) <math>420 g</math> (in <math>kg</math>) | |||
Erkläre deiner/m Partner/in deinen Rechenweg mithilfe des Merksatzes. Falls du dabei Probleme hast, schaue dir die Lösung an. | |||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]]''Wenn du mit der Aufgabe fertig bist, schreibe das Beispiel mit Lösung auf dein Arbeitsblatt.'' | |||
{{Lösung versteckt|1= a) <math>2,68m = 26,8dm</math>, da in eine kleinere Maßeinheit überführt werden soll, mit <math>1m = 10dm</math>, muss das Komma eine Stelle nach rechts verschoben werden. | |||
b) <math>420g = 0,42kg</math>, da in eine größere Maßeinheit überführt werden soll, mit <math>1000g = 1kg</math>, muss das Komma drei Stellen nach links verschoben werden.|2=Lösung|3=Lösung verbergen}}|Aufgabe | |||
| Farbe = {{Farbe|gelb}} | |||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (**) Aufgabe 14: Umrechnen von Größen|{{LearningApp|width=100%|height=500px|app=35502421}}|Aufgabe | ||
| Farbe = #CD2990 | | Farbe = #CD2990 | ||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (***) Aufgabe 15: Rechnen mit Größen|{{LearningApp|width=100%|height=500px|app=35497640}}|Aufgabe | ||
| Farbe = #5E43A5 | | Farbe = #5E43A5 | ||
}} | }} | ||
== | ==Teste dich!== | ||
===Teste dich zum Rechnen mit Dezimalzahlen=== | |||
'''Beachte:''' Es können auch mehrere Antwortmöglichkeiten richtig sein. | |||
<quiz display="simple"> | |||
=== | { Welche Stelle besitzt die "<math>4</math>" in <math>327,246</math>? } | ||
< | - Zehntel (z) <math>\frac{1}{10}</math> | ||
- Tausendstel (t) <math>\frac{1}{1000}</math> | |||
+ Hundertstel (h) <math>\frac{1}{100}</math> | |||
{ Wie lässt sich <math>0,75</math> noch darstellen? } | |||
+ <math>75\%</math> | |||
+ <math>\frac{75}{100}</math> | |||
- <math>\frac{75}{10}</math> | |||
{{ | |||
=== | { Wie lautet die Zahl <math>16,783</math> auf den Zehntel gerundet? } | ||
{ | + <math>16,8</math> | ||
- <math>16,78</math> | |||
- <math>16,7</math> | |||
{ Welche Aufgaben haben das gleiche Ergebnis? } | |||
+ <math>1,76 + 4,24</math> | |||
- <math>2,43 + 3,67</math> | |||
+ <math>5,32 + 0,68</math> | |||
- <math>3,12 + 3,08</math> | |||
{ Was ergibt <math>3,2 \cdot 2,3</math>? } | |||
- <math>6,6</math> | |||
}} | - <math>5,5</math> | ||
+ <math>7,36</math> | |||
- <math>11,5</math> | |||
</quiz> | |||
===Teste dich zum Umgang mit Größen=== | |||
'''Beachte:''' Es können auch mehrere Antwortmöglichkeiten richtig sein. | |||
<quiz display="simple"> | |||
{ Wandle in die nächstkleinere Einheit um: <math>3,25kg</math>} | |||
- <math>32,5mg</math>. | |||
- <math>0,00325t</math>. | |||
+ <math>3250g</math>. | |||
{ Berechne: <math>5,3m</math> <math>+ 123cm</math> } | |||
+ <math>6,53m</math> | |||
- <math>5,423m</math> | |||
- <math>176cm</math> | |||
+ <math>653cm</math> | |||
</quiz> | |||
<big> | |||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Kleine_Lernstandserhebung_zur_Doppeljahrgangsstufe_5/6}} | |||
<big> | |||
Aktuelle Version vom 7. Juni 2024, 08:00 Uhr
Einführung
Dezimalzahlen tauchen in unserem Alltag fast überall auf: im Supermarkt, beim Wiegen von Lebensmitteln, beim Messen deiner Körpergröße oder an der Tankstelle mit deinen Eltern. Deswegen kannst du die Dezimalzahlen und den Umgang mit Größen in diesem Lernpfad mit den wichtigsten Begriffen und Rechengesetzen wiederholen.
Erinnerst du dich noch an die Dezimalzahlen?
Vor- und Nachkommastelle in der Stellenwerttafel
Umgang mit Größen
Dezimalzahlen in der Welt der Größen
Drei Darstellungszahlen einer rationalen Zahl
Das Geheimnis des Rundens von Dezimalzahlen
Rechengesetze
Addition und Subtraktion von Dezimalzahlen
Multiplikation von Dezimalzahlen
Verhältnisse von Größen
Teste dich!
Teste dich zum Rechnen mit Dezimalzahlen
Beachte: Es können auch mehrere Antwortmöglichkeiten richtig sein.
Teste dich zum Umgang mit Größen
Beachte: Es können auch mehrere Antwortmöglichkeiten richtig sein.