Benutzer:Judith Uni MS-13/Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
(Erste Erstellung) Markierung: Quelltext-Bearbeitung 2017 |
(Backup) Markierung: Quelltext-Bearbeitung 2017 |
||
| (13 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Testseite== | |||
<span style="color:green">Dieser Text ist grün</span> | <span style="color:green">Dieser Text ist grün</span> und toll | ||
und so | |||
{{Box-spezial | |||
|Titel=Brüche | |||
|Inhalt= <math> \frac {1+x^{2-x}}{4+x} </math> | |||
|Farbe= #836FFF | |||
|Hintergrund= #F5F5F5 | |||
|Icon= {{Icon_pdf}} | |||
}} | |||
{{Box|Überschrift|Inhalt|Arbeitsmethode | |||
| Farbe = #CD2990 | |||
}} | |||
<div class="multiplechoice-quiz"> | |||
Wie kann man <math>\frac3 4</math> noch darstellen? (!<math>\frac 4 3</math>) (<math>\frac{9}{12}</math>) (<math>0,75</math>) (!<math>0,9</math>) | |||
</div> | |||
{{Lösung versteckt|1=ich bin versteckt|2=klick auf mich|3=Lass mich verschwinden}} | |||
{{LearningApp|width=100%|height=500px|app=2797556}} | |||
==GeoGebra== | |||
{{Box-spezial | |||
|Titel= | |||
|Inhalt=<ggb_applet id="bsZerbZE" width="700" height="400" border="888888" /> | |||
Was ist größer? <math>\frac4 7</math> oder <math>\frac 3 8</math> | |||
<div class="multiplechoice-quiz"> (!<math>\frac 3 8</math>) (<math>\frac 4 7</math>) </div> | |||
|Farbe= #836FFF | |||
|Hintergrund= #F5F5F5 | |||
}} | |||
{{Box | |||
| 1 = Info | |||
| 2 = In diesem Lernpfadkapitel <Brüche und Bruchrechnung> kannst du wiederholen, was Brüche sind und wie du mit ihnen rechnest. Du findest Inhalte dazu, was Brüche sind, wie du sie der Größe nach ordnest, wie du sie kürzen und erweitern kannst und wie man sie addiert (+) und subtrahiert (-). | |||
Für die Bearbeitung dieses Kapitels benötigst du das Arbeitsblatt zu den Brüchen und einen Stift. | |||
Bei den Aufgaben unterscheiden wir folgende Typen: | |||
* In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | |||
* Aufgaben in '''<span style="color: #CD2990">pinker</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | |||
* Und Aufgaben mit '''<span style="color: #5E43A5">lilanem</span>''' Streifen sind '''Knobelaufgaben'''. | |||
Viel Erfolg! | |||
| 3 = Kurzinfo | |||
}} | |||
[[Datei:Bildschirmfoto 2024-05-04 um 12.09.08.png|mini|200x200px]] | |||
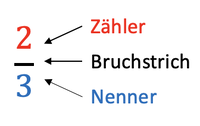
{{Box|Merksatz: Anteile von Brüchen|Brüche sind Teile eines Ganzen. Der <span style="color: blue"> Nenner </span> gibt an, in wie viele gleich große Teile das Ganze aufgeteilt wurde. Der <span style="color: red"> Zähler </span> gibt an, um wie viele Teile des Ganzen es geht. | |||
| Farbe = {{Farbe|grün|dunkel}} | |||
}}{{Box|Merksatz: <Bruchteile von Größen>|Der Bruchteil einer Größe beschreibt einen bestimmten Anteil von einer Größe wie Meter, Kilogramm oder Euro. Um einen Bruchteil einer Größe zu berechnen, musst du 1. durch den Nenner dividieren und dann 2. mit dem Zähler multiplizieren. Manchmal musst du auch zuerst in eine kleinere Einheit umrechnen, also beispielsweise Meter in Zentimeter oder Stunden in Minuten umwandeln.|Merksatz | |||
| Farbe = {{Farbe|grün|dunkel}} | |||
}} | |||
{{Box|Beispiel: <Bruchteile von Größen>|<math> \frac{3}{4} </math> von <math> 120 km </math> | |||
<math> 120 km : 4 = 30 km </math>, also sind <math> 30 km \frac {1}{4} </math> von <math> 120 km </math> | |||
<math> 30 km \cdot 3 = 90 km </math>, also sind <math> 90 km \frac {3}{4} </math> von <math> 120 km </math>|Hervorhebung1 | |||
}} | |||
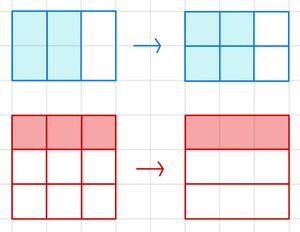
{{Box|Merksatz: <Brüche erweitern und kürzen>|So '''erweiterst''' du einen Bruch: | |||
Multipliziere Zähler und Nenner mit der gleichen Zahl. | |||
So '''kürzt''' du einen Bruch: | |||
Teile den Zähler und Nenner durch die gleichen Zahl ungleich 0. | |||
Der Wert des Bruchs bleibt dabei gleich.|Merksatz | |||
| Farbe = {{Farbe|grün|dunkel}} | |||
}} | |||
{{Box|Beispiel: <Brüche erweitern und kürzen>|<math>\frac{2}{3} = \frac{2}{3} \cdot \frac {2}{2} = \frac{4}{6}</math> | |||
<math>\frac{3}{9} = \frac{3}{9} : \frac {3}{3} = \frac{1}{3}</math> | |||
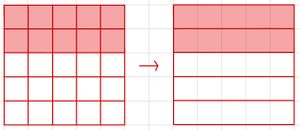
[[Datei:Darstellung_kürzen_erweitern.jpg|links|rahmenlos]]|Hervorhebung1 | |||
}} | |||
Probiere es doch gleich mal aus! | |||
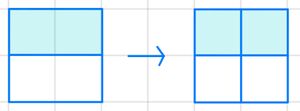
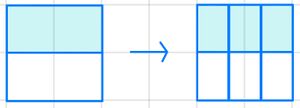
{{Box|Aufgabe <Nummer>: <Kästchen erweitern>|Notiere auf deinem Arbeitsblatt: | |||
Gib an, wie die Anteile der Kästchen als Bruch aussehen und mit welcher Zahl erweitert wurde. | |||
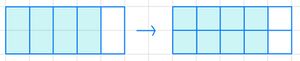
'''a)''' [[Datei:1-2 zu 2-4.jpg|zentriert|rahmenlos]] | |||
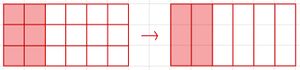
'''b)''' [[Datei:1-2zu3-6.jpg|zentriert|rahmenlos]] | |||
'''c)''' [[Datei:1-3zu4-12.jpg|zentriert|rahmenlos]] | |||
'''d)''' [[Datei:2-3zu12-18.jpg|zentriert|rahmenlos]] | |||
'''e)''' [[Datei:4-5zu8-10.jpg|zentriert|rahmenlos]] | |||
{{Lösung versteckt|1='''a)''' <math> \frac 12 = \frac 12 \cdot \frac 22 = \frac 24 </math> | |||
Es wurde mit <math>2</math> erweitert. | |||
'''b)''' <math> \frac 12 = \frac 12 \cdot \frac 33 = \frac 36 </math> | |||
Es wurde mit <math>3</math> erweitert. | |||
'''c)''' <math> \frac 13 = \frac 13 \cdot \frac 44 = \frac {4} {12} </math> | |||
Es wurde mit <math>4</math> erweitert. | |||
'''d)''' <math> \frac 23 = \frac 23 \cdot \frac 66 = \frac {12} {18} </math> | |||
Es wurde mit <math>6</math> erweitert. | |||
'''e)''' <math> \frac 45 = \frac 45 \cdot \frac 22 = \frac {8} {10} </math> | |||
Es wurde mit <math>2</math> erweitert. |2=Lösung anzeigen| | |||
3=Lösung verstecken}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||
{{Box|Aufgabe <Nummer>: <Kästchen kürzen>|Notiere auf deinem Arbeitsblatt: | |||
Gib an, wie die Anteile der Kästchen als Bruch aussehen und mit welcher Zahl gekürzt wurde. | |||
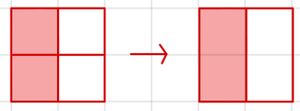
'''a)''' [[Datei:2-4 zu 1-2.jpg|zentriert|rahmenlos]] | |||
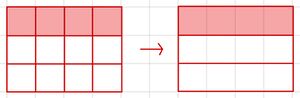
'''b)''' [[Datei:4-12zu1-3.jpg|zentriert|rahmenlos]] | |||
'''c)''' [[Datei:6-18zu2-6.jpg|zentriert|rahmenlos]] | |||
'''d)''' [[Datei:5-5zu1-1.jpg|zentriert|rahmenlos]] | |||
'''e)''' [[Datei:10-25zu2-5.jpg|zentriert|rahmenlos]] | |||
{{Lösung versteckt|1='''a)''' <math> \frac 24 = \frac 24 : \frac 22 = \frac 12 </math> | |||
Es wurde mit <math>2</math> gekürzt. | |||
'''b)''' <math> \frac {4} {12} = \frac {4}{12} : \frac 44 = \frac 13 </math> | |||
Es wurde mit <math>4</math> gekürzt. | |||
'''c)''' <math> \frac {6}{18} = \frac {6}{18} : \frac 33 = \frac {2} {6} </math> | |||
Es wurde mit <math>3</math> gekürzt. | |||
'''d)''' <math> \frac 55 = \frac 55 : \frac 55 = \frac 11 </math> | |||
Es wurde mit <math>5</math> gekürzt. | |||
'''e)''' <math> \frac {10}{25} = \frac {10}{25} : \frac 55 = \frac {2} {5} </math> | |||
Es wurde mit <math>5</math> gekürzt. |2=Lösung anzeigen| | |||
3=Lösung verstecken}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||
{{Box|Aufgabe <Nummer>: <Brüche erweitern und kürzen>|Ordne zu, womit hier gekürzt oder erweitert wurde. Wenn du fertig bist, klicke auf das Icon unten rechts, um deine Lösung zu überprüfen. | |||
{{LearningApp|width=100%|height=500px|app=7674438}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||
{{Box|Aufgabe <Nummer>: <Brüche ergänzen>|Gib auf deinem Arbeitsblatt die fehlenden Zahlen an. | |||
'''a)''' <math>\frac 16 = \frac{5}{} \hspace{1cm} </math> | |||
'''b)''' <math>\frac 25 = \frac{10}{} \hspace{1cm} </math> | |||
'''c)''' <math>\frac 37 = \frac{}{49} \hspace{1cm} </math> | |||
'''d)''' <math>\frac 79 = \frac{}{99} \hspace{1cm} </math> | |||
'''e)''' <math>\frac {6} {19} = \frac{24}{} </math> | |||
'''f)''' <math>\frac {3}{} = \frac{12}{28} \hspace{1cm} </math> | |||
'''g)''' <math>\frac {5}{} = \frac{25}{45} \hspace{1cm} </math> | |||
'''h)''' <math>\frac {}{13} = \frac{44}{52} \hspace{1cm} </math> | |||
'''i)''' <math>\frac {}{4} = \frac{75}{100} \hspace{1cm} </math> | |||
'''j)''' <math>\frac {5}{} = \frac{70}{84} </math> | |||
{{Lösung versteckt|1= Denk daran, dass beim Erweitern/Kürzen der Zähler und der Nenner immer mit der gleichen Zahl multipliziert (<math>\cdot</math>)/dividiert (:) wird.|2= Tipp anzeigen|3= Tipp verstecken}} | |||
{{Lösung versteckt|1='''a)''' 30 <math>\hspace{0.5cm}</math> '''b)''' 25<math>\hspace{0.5cm}</math> '''c)''' 21 | |||
<math>\hspace{0.5cm}</math> '''d)''' 77<math>\hspace{0.5cm}</math> '''e)''' 76 <math>\hspace{0.5cm}</math> | |||
'''f)''' 7 <math>\hspace{0.5cm}</math> '''g)''' 9 <math>\hspace{0.5cm}</math> '''h)''' 11 <math>\hspace{0.5cm}</math> '''i)''' 3 <math>\hspace{0.5cm}</math>'''j)''' 6|2=Lösung anzeigen| | |||
3=Lösung verstecken}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||