Benutzer:Stoll-Gym10Erfurt/Mathematik10/Trigonometrische Berechnungen/Allgemeine Dreiecke: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
===Sinus- und Kosinussatz=== | ===Sinus- und Kosinussatz=== | ||
{{Box-spezial | {{Box-spezial | ||
|Titel= Einführende Bemerkungen | |Titel= Einführende Bemerkungen | ||
|Inhalt= Die Berechnungen in den vorherigen Abschnitten gelten nur in rechtwinkligen Dreiecken. Nun lernen wir Möglichkeiten kennen, wie man fehlende Größen auch in allgemeinen Dreiecken berechnen kann. | |Inhalt= <big>Die Berechnungen in den vorherigen Abschnitten gelten nur in rechtwinkligen Dreiecken. Nun lernen wir Möglichkeiten kennen, wie man fehlende Größen auch in allgemeinen Dreiecken berechnen kann.</big> | ||
|Farbe= #FF0000 | |Farbe= #FF0000 | ||
|Hintergrund= #00FF00 | |Hintergrund= #00FF00 | ||
|Icon= <span class="brainy hdg-graduation-hat"></span> | |Icon= <span class="brainy hdg-graduation-hat"></span> | ||
}} | }} | ||
{{Box-spezial | {{Box-spezial | ||
|Titel= Sinus- und Kosinussatz | |Titel= Sinus- und Kosinussatz | ||
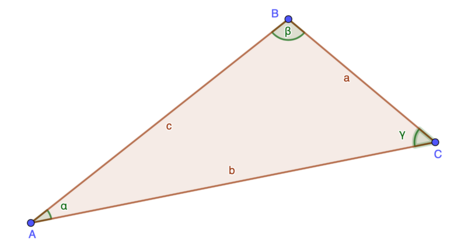
|Inhalt= Beide Sätze stellen Beziehungen zwischen Seitenlängen und Winkeln in beliebigen Dreiecken dar. Sie gelten für beliebige Dreiecke mit den Seiten a, b und c, sowie den Winkeln <math>\alpha, \beta \; und \; \gamma. </math> | |Inhalt= <big>Beide Sätze stellen Beziehungen zwischen Seitenlängen und Winkeln in beliebigen Dreiecken dar. Sie gelten für beliebige Dreiecke mit den Seiten a, b und c, sowie den Winkeln <math>\alpha, \beta \; und \; \gamma. </math> </big> | ||
|Farbe= #FF0000 | |Farbe= #FF0000 | ||
|Hintergrund= #00FF00 | |Hintergrund= #00FF00 | ||
|Icon= <span class="brainy hdg-head-exclamation"></span> | |Icon= <span class="brainy hdg-head-exclamation"></span> | ||
}} | }} | ||
[[Datei:Dreieck allgemein.png|zentriert|mini|450x450px]] | [[Datei:Dreieck allgemein.png|zentriert|mini|450x450px]] | ||
{{Box-spezial | {{Box-spezial | ||
|Titel= Sinussatz | |Titel= Sinussatz | ||
|Inhalt= <math> \frac{a}{sin(\alpha)} = \frac{b}{sin(\beta)} = \frac{c}{sin(\gamma)} . </math> | |Inhalt= <big><math> \frac{a}{sin(\alpha)} = \frac{b}{sin(\beta)} = \frac{c}{sin(\gamma)} . </math> </big> | ||
|Farbe= #FF0000 | |Farbe= #FF0000 | ||
|Hintergrund= #00FF00 | |Hintergrund= #00FF00 | ||
| Zeile 27: | Zeile 24: | ||
{{Box-spezial | {{Box-spezial | ||
|Titel= Kosinussatz | |Titel= Kosinussatz | ||
|Inhalt= <math> c^2=a^2+b^2-2ab \cdot cos(\gamma) </math> <br/> | |Inhalt= <big> <math> c^2=a^2+b^2-2ab \cdot cos(\gamma) </math> <br/> | ||
<math> b^2=a^2+c^2-2ac \cdot cos(\beta) </math> <br/> | <math> b^2=a^2+c^2-2ac \cdot cos(\beta) </math> <br/> | ||
<math> a^2=b^2+c^2-2bc \cdot cos(\alpha) </math> < | <math> a^2=b^2+c^2-2bc \cdot cos(\alpha) </math> <big> | ||
|Farbe= #FF0000 | |Farbe= #FF0000 | ||
|Hintergrund= #00FF00 | |Hintergrund= #00FF00 | ||
|Icon= <span class="brainy hdg-head-exclamation"></span> | |Icon= <span class="brainy hdg-head-exclamation"></span> | ||
}} | }} | ||
=== Lehrer Schmidt erklärt den Sinus- und Kosinussatz === | === Lehrer Schmidt erklärt den Sinus- und Kosinussatz === | ||
{{Box-spezial | {{Box-spezial | ||
| Zeile 42: | Zeile 38: | ||
|Farbe= #0077dd | |Farbe= #0077dd | ||
|Hintergrund= #A8DF4A | |Hintergrund= #A8DF4A | ||
|Icon= <span class="brainy hdg- | |Icon= <span class="brainy hdg-screen01"></span> | ||
}} | }} | ||
{{Box-spezial | {{Box-spezial | ||
|Titel= Kosinussatz | |Titel= Kosinussatz | ||
| Zeile 51: | Zeile 46: | ||
|Farbe= #0077dd | |Farbe= #0077dd | ||
|Hintergrund= #A8DF4A | |Hintergrund= #A8DF4A | ||
|Icon= <span class="brainy hdg- | |Icon= <span class="brainy hdg-screen01"></span> | ||
}} | }} | ||
=== Berechnungen in Allgemeinen Dreiecken === | === Berechnungen in Allgemeinen Dreiecken === | ||
{{Box-spezial | {{Box-spezial | ||
| Zeile 61: | Zeile 55: | ||
|Farbe= #0077dd | |Farbe= #0077dd | ||
|Hintergrund= #A8DF4A | |Hintergrund= #A8DF4A | ||
|Icon= <span class="brainy hdg- | |Icon= <span class="brainy hdg-screen01"></span> | ||
}} | }} | ||