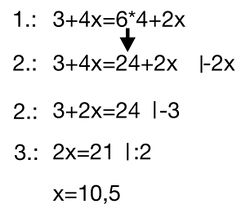|
|
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| [[Benutzer:Stoll-Gym10Erfurt|Startseite]]<br /> | | [[Benutzer:Stoll-Gym10Erfurt|1.Startseite]]<br /> |
| [[Benutzer:HAG-S17|Einleitung mit Inhaltsverzeichnis]]<br /> | | [[Benutzer:HAG-S17|2.Einleitung mit Inhaltsverzeichnis]]<br /> |
| [[Brüche|Brüche]]<br /> | | [[Benutzer:HAG-S17/2.Brüche|3.Brüche]]<br /> |
| [[schriftliches Rechnen|schriftliches Rechnen]]<br /> | | [[Benutzer:HAG-S17/schriftliches Rechnen|4.schriftliches Rechnen]]<br /> |
| <br /> | | <br /> |
|
| |
|
| Zeile 18: |
Zeile 18: |
| }} | | }} |
|
| |
|
| c
| | <br /> |
| {{Box-spezial | | {{Box-spezial |
| |Titel= Definition Gleichung | | |Titel= Definition Gleichung |
| Zeile 102: |
Zeile 102: |
| | | | | |
| |Arbeitsmethode}} | | |Arbeitsmethode}} |
| | |
| | {{Box|Übung 2: Finde die Paare |
| | Bearbeite die folgende LearningApp: Terme und Gleichungen |
| | {{LearningApp|app=pxyw985ht23 |
| | |width=100%|height=500px}} |
| | | |
| | | |
| | |Arbeitsmethode}} |
| | |
|
| |
|
|
| |
|
Aktuelle Version vom 2. Mai 2024, 08:29 Uhr
1.Startseite
2.Einleitung mit Inhaltsverzeichnis
3.Brüche
4.schriftliches Rechnen
Terme und Gleichungen
Was ist das?
Definition Term
Ein Term ist eine sinnvolle Kombination aus Zahlen, Variablen, mathematischen Verknüpfungen(+-*:) und Klammern. Relationszeichen dürfen in Termen nicht vorhanden sein. Ein Term kann nur aus einer Zahl oder Variable bestehen.
Definition Gleichung
Eine Gleichung ist ein mathematischer Ausdruck, bestehend aus zwei Termen, die durch das Gleichheitszeichen verbunden sind.
Zusammenfassen bei Zahl und Zahl
Wie der Begriff "Zusammenfassen" schon verrät, geht es darum den Term einfacher darzustellen. Wenn vor der Variablen keine Zahl steht, muss gedanklich eine 1 gesetzt werden.
- Einfach zusammenrechnen
- Punkt vor Strich beachten
- Wenn man nichts zusammenfassen kann ausmultiplizieren, ausklammern oder binomische Formeln anwenden.
Zusammenfassen bei Variable und Zahl
- Wenn eine Variable keine Zahl hat, muss gedanklich eine 1 davor geschrieben werden.
- Wenn man dann zwei Kombinationen aus Zahl und Variable hat, kann man diese Zusammenfasen
- Die zwei Zahlen kann man einfach mit dem Rechenzeichen berechnen. Diese können unterschiedlich sein.
- Bei + oder - muss die Variable dieselbe bleiben. Diese bleibt im Ergebnis erhalten. Bei * oder : können die Variablen unterschiedlich sein.
Übung 1: Ordne richtig zu!
Bearbeite die folgende LearningApp: Terme und Gleichungen
Wie löse ich jetzt Gleichungen?
Gleichung lösen
Eine Gleichung kann durch Probieren oder der Äquivalenzumformung gelöst werden. Das Ziel ist es eine Variable zu bestimmen.
Probieren
Durch systematisches Einsetzen von Zahlen für die Variable kommt man zum Ergebnis. Problem: Dauert zu lange und es können mögliche Ergebnisse verloren gehen.
Äquivalenzumformung
Auf beiden Seiten der Gleichung muss die selbe Operation durchgeführt werden. Dazu schreibt man einen sogenannten Operationsstrich hinter die Gleichung, daneben das Rechenzeichen und da neben die Zahl oder Variable oder beides. Ziel ist es auf eine Seite der Gleichung nur Zahlenterme zu haben und auf der anderen Seite nur die zu bestimmende Variable.
Tutorial
- Zuerst wird alles zusammengefasst, was geht.
- Jetzt wendet man die Äquivalenzumformung an
- Wenn dann alle Zahlen auf der einen Seite sind und alle Variablen auf der anderen, muss durch multiplizieren und dividieren die Variable bestimmt werden.(vor der Variable muss eine 1 stehen)
Übung 2: Finde die Paare
Bearbeite die folgende LearningApp: Terme und Gleichungen
Übung 2: Finde die Paare
Bearbeite die folgende LearningApp: Terme und Gleichungen
Übung 3: Fülle die Lücken
Bearbeite die folgende LearningApp: Terme und Gleichungen