Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden vermessen: Unterschied zwischen den Versionen
Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (35 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box | {{Box | ||
|1=Info | |1=Info | ||
| Zeile 17: | Zeile 13: | ||
==Wiederholung== | ==Wiederholung== | ||
{{Box|1=Info|2=Um die Oberfläche einer Pyramide zu bestimmen, ist es wichtig, dass du weißt, wie man den Flächeninhalt von Rechtecken und von Dreiecken bestimmt. Wenn du dich noch daran erinnerst, wie man diesen bestimmt, kannst du direkt zu Aufgabe 5 gehen. Wenn du dir noch etwas unsicher bist und eine kurze Wiederholung brauchst, bearbeite die folgenden Aufgaben (Aufgaben 1,2,3 und 4).|3=Kurzinfo}} | {{Box|1=Info|2=Um die Oberfläche einer Pyramide zu bestimmen, ist es wichtig, dass du weißt, wie man den Flächeninhalt von Rechtecken und von Dreiecken bestimmt. Wenn du dich noch daran erinnerst, wie man diesen bestimmt, kannst du direkt zu Aufgabe 5 gehen. Wenn du dir noch etwas unsicher bist und eine kurze Wiederholung brauchst, bearbeite die folgenden Aufgaben (Aufgaben 1, 2, 3 und 4).|3=Kurzinfo}} | ||
===Rechteckigen Flächeninhalt berechnen=== | ===Rechteckigen Flächeninhalt berechnen=== | ||
{{Box|Aufgabe 1: Flächeninhalt vom Rechteck|Berechne den Flächeninhalt des folgenden | {{Box|Aufgabe 1: Flächeninhalt vom Rechteck|Berechne den Flächeninhalt des folgenden Rechtecks (denke auch daran, die richtige Einheit anzugeben): {{LearningApp|width=100%|height=500px|app=pay5n3goj22}} | ||
{{Lösung versteckt|1=Zur Berechnung des Flächeninhaltes benötigst du nicht die Diagonale.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | {{Lösung versteckt|1=Zur Berechnung des Flächeninhaltes benötigst du nicht die Diagonale.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | ||
| Zeile 26: | Zeile 22: | ||
{{Lösung versteckt|1=Die Formel zur Berechnung eines rechteckigen Flächeninhaltes lautet: <math>A=a \cdot b</math>|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | {{Lösung versteckt|1=Die Formel zur Berechnung eines rechteckigen Flächeninhaltes lautet: <math>A=a \cdot b</math>|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1=<math>A=4 \text{ cm} \cdot 3 \text{ cm} =12 \text{ | {{Lösung versteckt|1=<math>A=4 \text{ cm} \cdot 3 \text{ cm} =12 \text{ cm}^{2}</math>|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Arbeitsmethode |Farbe={{Farbe|orange}} }} | | Arbeitsmethode |Farbe={{Farbe|orange}} }} | ||
| Zeile 36: | Zeile 32: | ||
{{Lösung versteckt|1=Die Formel zur Berechnung eines dreieckigen Flächeninhaltes lautet: <math>A=\tfrac{g \cdot h}{2}</math>|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | {{Lösung versteckt|1=Die Formel zur Berechnung eines dreieckigen Flächeninhaltes lautet: <math>A=\tfrac{g \cdot h}{2}</math>|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1=<math>A= \tfrac{4 \text{ cm} \cdot 6 \text{ cm}}{2} =12 \text{ | {{Lösung versteckt|1=<math>A= \tfrac{4 \text{ cm} \cdot 6 \text{ cm}}{2} =12 \text{ cm}^{2}</math>|2=Lösung anzeigen|3=Lösung verbergen}}| Arbeitsmethode |Farbe={{Farbe|orange}} }} | ||
{{Box|1=Info|2=In den Aufgaben 3 und 4 hast du noch einmal die Möglichkeit, das Bestimmen von recht- und dreieckigen Flächeninhalten zu üben. Solltest du dich schon sicher fühlen, kannst du auch direkt mit Aufgabe 5 weitermachen.|3=Kurzinfo}} | {{Box|1=Info|2=In den Aufgaben 3 und 4 hast du noch einmal die Möglichkeit, das Bestimmen von recht- und dreieckigen Flächeninhalten zu üben. Solltest du dich schon sicher fühlen, kannst du auch direkt mit Aufgabe 5 weitermachen.|3=Kurzinfo}} | ||
{{Box | Aufgabe 3: Rechteckige Flächeninhalte | {{Box | Aufgabe 3: Rechteckige Flächeninhalte| | ||
Berechne den Flächeninhalt folgender Rechtecke. | |||
'''a)''' <math>a=7\text{ m}, b=5\text{ m}</math> | '''a)''' <math>a=7\text{ m}, b=5\text{ m}</math> | ||
{{Lösung versteckt|1=<math>A=35\text{ m}^{2}</math>|2=Lösung a) anzeigen|3=Lösung a) verbergen}} | {{Lösung versteckt|1=<math>A=7 \text{ m} \cdot 5 \text{ m} =35 \text{ m}^{2}</math>|2=Lösung a) anzeigen|3=Lösung a) verbergen}} | ||
'''b)''' <math>a=90\text{ dm}, b=2\text{ m}</math> | '''b)''' <math>a=90\text{ dm}, b=2\text{ m}</math> | ||
{{Lösung versteckt|1=<math>A=18\text{ m}^{2} | {{Lösung versteckt|1=Berechnung in m: <math>A=9 \text{ m} \cdot 2 \text{ m} =18 \text{ m}^{2}</math> | ||
oder | |||
Berechnung in dm: <math>A=90 \text{ dm} \cdot 20 \text{ dm} =1800\text{ dm}^{2}</math>|2=Lösung b) anzeigen|3=Lösung b) verbergen}} | |||
| Arbeitsmethode|Farbe={{Farbe|orange}}}} | | Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
{{Box | Aufgabe 4: Dreieckige Flächeninhalte | {{Box | Aufgabe 4: Dreieckige Flächeninhalte| | ||
Berechne den Flächeninhalt folgender Dreiecke. | |||
'''a)''' <math>g=16\text{ m}, h=7\text{ m}</math> | |||
{{Lösung versteckt|1=<math>A= \tfrac{16 \text{ m} \cdot 7 \text{ m}}{2} =56 \text{ m}^{2}</math>|2=Lösung a) anzeigen|3=Lösung a) verbergen}} | |||
'''b)''' <math>g=4\text{ m}, h=500\text{ cm}</math> | |||
{{Lösung versteckt|1=Berechnung in m: <math>A= \tfrac{4 \text{ m} \cdot 5 \text{ m}}{2} =10 \text{ m}^{2}</math> | |||
oder | |||
Berechnung in dm: <math> A=\tfrac{40 \text{ dm} \cdot 50 \text{ dm}}{2}=1000\text{ dm}^{2}</math> | |||
oder | |||
Berechnung in cm: <math>A=\tfrac{400 \text{ cm} \cdot 500 \text{ cm}}{2}=100000\text{ cm}^{2}</math>|2=Lösung b) anzeigen|3=Lösung b) verbergen}} | |||
| Arbeitsmethode|Farbe={{Farbe|orange}}}} | | Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
{{Box|Aufgabe 5: Formeln notieren|[[Datei:Grundlagen-bearbeiten.png|30px|middle]] ''' | {{Box|Aufgabe 5: Formeln notieren|Trage die Formeln zur Berechnung rechteckiger und dreieckiger Flächeninhalte ein. | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | |||
{{Lösung versteckt| | |||
Die Formel zur Berechnung eines rechteckigen Flächeninhaltes lautet: <math>A=a \cdot b</math> | |||
Die Formel zur Berechnung eines dreieckigen Flächeninhaltes lautet: <math>A=\tfrac{g \cdot h}{2}</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| Arbeitsmethode |Farbe={{Farbe|orange}} }} | | Arbeitsmethode |Farbe={{Farbe|orange}} }} | ||
==Oberflächeninhalte berechnen== | ==Oberflächeninhalte berechnen== | ||
{{Box | 1=Aufgabe 6: Materialien berechnen | | |||
Lies dir eine der folgenden Situationsbeschreibungen durch | 2='''a)''' Lies dir eine der folgenden Situationsbeschreibungen durch. | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-3"> | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
[[File:Louvre Museum (228021559).jpeg|500px|rahmenlos|Louvre_Museum_(228021559)]] | [[File:Louvre Museum (228021559).jpeg|500px|rahmenlos|Louvre_Museum_(228021559)]] | ||
| Zeile 79: | Zeile 97: | ||
|2=Louvre|3=Einklappen}} | |2=Louvre|3=Einklappen}} | ||
</div> | </div> | ||
<div class="width-1-3"> | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
[[File:Kheops-Pyramid.jpg|500px|rahmenlos|Kheops-Pyramid|alt=Kheops-Pyramid.jpg]] | [[File:Kheops-Pyramid.jpg|500px|rahmenlos|Kheops-Pyramid|alt=Kheops-Pyramid.jpg]] | ||
Die Cheops-Pyramide ist die älteste und größte der drei Pyramiden von Gizeh und wird deshalb auch als „Große Pyramide“ bezeichnet. Diese höchste Pyramide der Welt wurde als Grabmal für den Pharao Cheops etwa 2620 v. Chr. errichtet und gilt heutzutage als eines der sieben Weltwunder der Antike. Natürlich mussten ausreichend '''Steine''' gehauen werden, um den Bau zu vollenden. Der zuständige Untertan stand vor der Aufgabe, die passende Anzahl zu berechnen. | Die Cheops-Pyramide ist die älteste und größte der drei Pyramiden von Gizeh und wird deshalb auch als „Große Pyramide“ bezeichnet. Diese höchste Pyramide der Welt wurde als Grabmal für den Pharao Cheops etwa 2620 v. Chr. errichtet und gilt heutzutage als eines der sieben Weltwunder der Antike. Natürlich mussten ausreichend '''Steine''' gehauen werden, um den Bau zu vollenden. Der zuständige Untertan stand vor der Aufgabe, die passende Anzahl zu berechnen. | ||
|2= | |2=Cheops-Pyramide|3=Einklappen}} | ||
</div> | </div> | ||
<div class="width-1-3"> | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
[[File:Münster, St.-Paulus-Dom -- 2019 -- 3536.jpg|500px|rahmenlos|Münster, St.-Paulus-Dom -- 2019 -- 3536]] | [[File:Münster, St.-Paulus-Dom -- 2019 -- 3536.jpg|500px|rahmenlos|Münster, St.-Paulus-Dom -- 2019 -- 3536]] | ||
| Zeile 91: | Zeile 109: | ||
|2=Kirchturm|3=Einklappen}} | |2=Kirchturm|3=Einklappen}} | ||
</div> | </div> | ||
</div> | </div> | ||
'''b)''' Überlege dir bei einer der Situationen, wie man das Problem mathematisch lösen könnte. Beschreibe dein Vorgehen auf einem Zettel in Stichpunkten. Hier sind keine Rechnungen erforderlich und du brauchst auch nicht zählen. | |||
Überlege dir bei einer der Situationen, wie man das Problem mathematisch lösen könnte. Beschreibe dein Vorgehen auf einem Zettel in Stichpunkten. Hier sind keine Rechnungen erforderlich und du brauchst auch nicht zählen. | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Die Gebäude sind allesamt Pyramiden haben vier '''gleichgroße, dreieckige''' Seitenflächen. Was benötigst du zum Berechnen einer solchen Seitenfläche? Muss die Grundfläche bei der Materialberechnung berücksichtigt werden? | Die Gebäude sind allesamt Pyramiden und haben vier '''gleichgroße, dreieckige''' Seitenflächen. Was benötigst du zum Berechnen einer solchen Seitenfläche? Muss die Grundfläche bei der Materialberechnung berücksichtigt werden? | ||
|2=Tipp|3=Tipp verbergen}} | |2=Tipp|3=Tipp verbergen}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| Zeile 114: | Zeile 128: | ||
<math> 4 \cdot A = 4 \cdot \frac{g \cdot h_g}{2} = 2 \cdot g \cdot h_g </math> | <math> 4 \cdot A = 4 \cdot \frac{g \cdot h_g}{2} = 2 \cdot g \cdot h_g </math> | ||
Man benötigt also nur die | Man benötigt also nur die Maße der Grundseite und der Höhe des Dreiecks, um den Flächeninhalt einer Seitenfläche zu bestimmen. Wenn man nun den Flächeninhalt kennt, den ein Materialstück benötigt, so kann man durch Teilen den Materialverbrauch für eine Seitenfläche berechnen. | ||
|2=Lösung|3=Lösung verbergen}} | |2=Lösung|3=Lösung verbergen}} | ||
| 3=Arbeitsmethode|Farbe={{Farbe|orange}}}} | |||
| Arbeitsmethode|Farbe={{Farbe|orange}}}} | |||
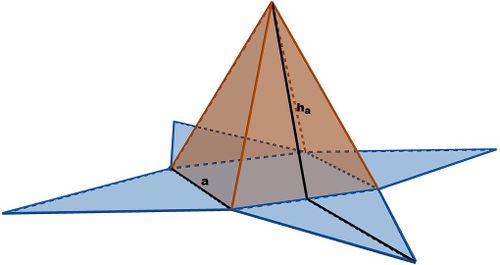
[[Datei:Pyramide Schrägbild.jpg|rahmenlos|mini|rechts|Schrägbild einer Pyramide mit angegebener Kantenlänge und Seitenhöhe]] | [[Datei:Pyramide Schrägbild.jpg|rahmenlos|mini|rechts|Schrägbild einer Pyramide mit angegebener Kantenlänge und Seitenhöhe]] | ||
| Zeile 139: | Zeile 152: | ||
Im Falle einer quadratischen Pyramide, welche ihre Spitze über der Mitte ihrer Grundfläche hat, ergibt sich für die Grundfläche die Fläche eines Quadrates und für ihre Mantelfläche die Flächeninhalte von vier gleich großen Dreiecken. | Im Falle einer quadratischen Pyramide, welche ihre Spitze über der Mitte ihrer Grundfläche hat, ergibt sich für die Grundfläche die Fläche eines Quadrates und für ihre Mantelfläche die Flächeninhalte von vier gleich großen Dreiecken. | ||
{{Box | Beispiel: Oberflächeninhalt berechnen | | {{Box | Beispiel: Quadratischen Oberflächeninhalt berechnen | | ||
Betrachte die Pyramide rechts, mit einer Kantenlänge von <math>a = 5\text{ cm}</math> und einer Seitenhöhe von <math>h_a = 6\text{ cm}</math>. | Betrachte die Pyramide rechts, mit einer Kantenlänge von <math>a = 5\text{ cm}</math> und einer Seitenhöhe von <math>h_a = 6\text{ cm}</math>. | ||
| Zeile 147: | Zeile 159: | ||
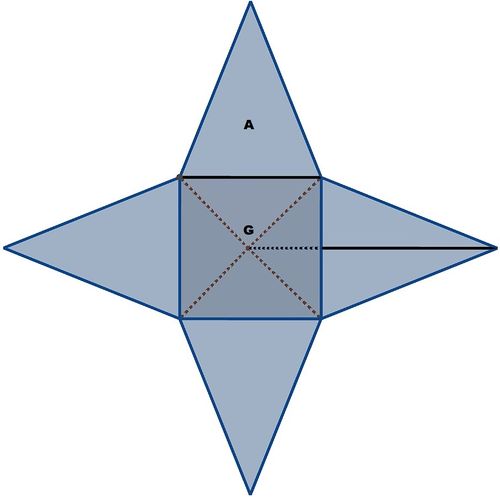
[[Datei:Pyramide Gitternetz mit Angaben.jpg|rahmenlos|500px|rechts|Gitternetz einer Pyramide mit angegebener Kantenlänge und Seitenhöhe.]] | [[Datei:Pyramide Gitternetz mit Angaben.jpg|rahmenlos|500px|rechts|Gitternetz einer Pyramide mit angegebener Kantenlänge und Seitenhöhe.]] | ||
'''Grundfläche G''': | '''Grundfläche <math>G</math>''': | ||
<math>G = a \cdot a</math> | <math>G = a \cdot a</math> | ||
| Zeile 155: | Zeile 167: | ||
<math>G = 25 \text{ cm}^2</math>. | <math>G = 25 \text{ cm}^2</math>. | ||
'''Seitenfläche A''': | '''Seitenfläche <math>A</math>''': | ||
<math>A = \frac{a\cdot h_a}{2} </math> | <math>A = \frac{a\cdot h_a}{2} </math> | ||
| Zeile 163: | Zeile 175: | ||
<math>A = 15\text{ cm}^2</math> | <math>A = 15\text{ cm}^2</math> | ||
'''Mantelfläche M''': | '''Mantelfläche <math>M</math>''': | ||
<math>M = 4 \cdot A</math> | <math>M = 4 \cdot A</math> | ||
| Zeile 171: | Zeile 183: | ||
<math>M = 60\text{ cm}^2</math>. | <math>M = 60\text{ cm}^2</math>. | ||
''' | '''Oberflächeninhalt <math>O</math>''': | ||
<math>O = G + M</math> | <math>O = G + M</math> | ||
| Zeile 186: | Zeile 198: | ||
{{Box | Aufgabe 8: Oberflächeninhalte verschiedener Pyramiden berechnen | | {{Box | Aufgabe 8: Oberflächeninhalte verschiedener Pyramiden berechnen | | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] ''' | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
{{Lösung versteckt|1= | |||
<div class="grid"> | |||
<div class="width-1-4"> | |||
'''a)''' | |||
'''Grundfläche <math>G</math>''': | |||
<math> G = a^2 </math> | |||
<math> G = 6^2 = 36 </math> | |||
'''Seitenfläche <math>A</math>''': | |||
<math> A = \frac{a \cdot h_a}{2} </math> | |||
<math> A = \frac{6 \cdot 7}{2} = 21 </math> | |||
'''Oberflächeninhalt <math>O</math>''': | |||
<math> O = G + 4 \cdot A </math> | |||
<math> O = 36 + 4 \cdot 21 = 120 </math> | |||
</div> | |||
<div class="width-1-4"> | |||
'''b)''' | |||
'''Seitenfläche <math>A_a</math>''': | |||
<math> A_a = \frac{a \cdot h_a}{2} </math> | |||
<math> A_a = \frac{8 \cdot 6,71}{2} = 26,84 </math> | |||
'''Seitenfläche <math>A_b</math>''': | |||
<math> A_b = \frac{b \cdot h_b}{2} </math> | |||
<math> A_b = \frac{6 \cdot 7,21}{2} = 21,63 </math> | |||
'''Mantelfläche <math>M</math>''': | |||
<math> M = 2 \cdot A_a + 2 \cdot A_b </math> | |||
<math> M = 2 \cdot 26,84 + 2 \cdot 21,63</math> | |||
<math> M = 96,94 </math> | |||
</div> | |||
<div class="width-1-4"> | |||
'''c)''' | |||
'''Grundfläche <math>G</math>''': | |||
<math> G = a \cdot b </math> | |||
<math> G = 6 \cdot 10 = 60 </math> | |||
'''Seitenfläche <math>A_a</math>''': | |||
<math> A_a = \frac{a \cdot h_a}{2} </math> | |||
<math> A_a = \frac{6 \cdot 8,6}{2} = 25,8 </math> | |||
'''Seitenfläche <math>A_b</math>''': | |||
<math> A_b = \frac{b \cdot h_b}{2} </math> | |||
<math> A_b = \frac{10 \cdot 7,62}{2} = 38,1 </math> | |||
'''Mantelfläche <math>M</math>''': | |||
<math> M = 2 \cdot A_a + 2 \cdot A_b </math> | |||
<math> M = 2 \cdot 25,8 + 2 \cdot 38,1 </math> | |||
<math> M = 127,8 </math> | |||
'''Oberflächeninhalt <math>O</math>''': | |||
<math> O = G + M </math> | |||
<math> O = 60 + 127,8 = 187,8 </math> | |||
</div> | |||
<div class="width-1-4"> | |||
'''d)''' | |||
'''Seitenfläche <math>A</math>''': | |||
<math> A = \frac{a \cdot h_a}{2} </math> | |||
<math> A = \frac{2 \cdot 4,72}{2} = 4,72 </math> | |||
'''Mantelfläche <math>M</math>''': | |||
<math> M = 6 \cdot A </math> | |||
<math> M = 6 \cdot 4,72 = 28,32 </math> | |||
</div> | |||
</div> | |||
|2=Lösungen|3=Lösungen verbergen}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | Aufgabe 9: Tetraeder? | | {{Box | Aufgabe 9: Tetraeder? | | ||
Azra hat zur Berechnung an einer Pyramide mit dreieckiger Grundfläche sehr viele Größen gemessen, um auf alles vorbereitet zu sein. Allerdings sollte sie nur den Oberflächeninhalt berechnen. | Azra hat zur Berechnung an einer Pyramide mit dreieckiger Grundfläche sehr viele Größen gemessen, um auf alles vorbereitet zu sein. Allerdings sollte sie nur den Oberflächeninhalt berechnen. | ||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Du kannst durch Klicken, Ziehen und Loslassen mit der Maus die Pyramide drehen. Außerdem kannst du auch die Zahlen genauso verschieben, um sie besser lesen zu können. | |||
<ggb_applet id="psnmcrma" width="1000" height="718" /> | <ggb_applet id="psnmcrma" width="1000" height="718" /> | ||
Kevin erwidert, dass dies ja viel zu viel Arbeit sei, da man doch nur eine der Seitenflächen benötigt. Schnell berechnet er: | Kevin erwidert, dass dies ja viel zu viel Arbeit sei, da man doch nur eine der Seitenflächen benötigt. Schnell berechnet er: | ||
| Zeile 237: | Zeile 349: | ||
==Pyramiden schätzen== | ==Pyramiden schätzen== | ||
Im Alltag kommt es manchmal vor, dass man nicht alle Angaben kennt, die man zur Bestimmung der Oberfläche benötigt. In diesem Abschnitt kannst du deshalb üben, einzelne Angaben oder auch den gesamten Flächeninhalt zu schätzen. Dabei kommt es nicht so sehr darauf an, dass du immer komplett richtig schätzt (das wäre ja auch so gut wie unmöglich), sondern, dass du ein Gefühl für die Größen entwickelst. | {{Box | ||
|1=Info | |||
|2=Im Alltag kommt es manchmal vor, dass man nicht alle Angaben kennt, die man zur Bestimmung der Oberfläche benötigt. In diesem Abschnitt kannst du deshalb üben, einzelne Angaben oder auch den gesamten Flächeninhalt zu schätzen. Dabei kommt es nicht so sehr darauf an, dass du immer komplett richtig schätzt (das wäre ja auch so gut wie unmöglich), sondern, dass du ein Gefühl für die Größen entwickelst. | |||
|3=Kurzinfo}} | |||
{{Box|Aufgabe 10: Oberfläche von Pyramiden schätzen|Ordne jedem Bild durch Schätzen den passenden Oberflächeninhalt zu (du musst hier nichts rechnen!) | {{Box|Aufgabe 10: Oberfläche von Pyramiden schätzen|Ordne jedem Bild durch Schätzen den passenden Oberflächeninhalt zu (du musst hier nichts rechnen!). Am Ende bleiben einige Werte übrig, da es mehr Werte als Bilder gibt. | ||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Durch Anklicken der Bilder werden diese größer. | |||
{{LearningApp|width=100%|height=500px|app=pnrcnm2fa22}} | |||
{{Lösung versteckt|Sortiere die Größen erstmal grob bevor du sie den Bildern zuordnest.|Tipp|Tipp verbergen}}| Arbeitsmethode |Farbe={{Farbe|orange}} }} | |||
{{Box|Aufgabe 11: Karlsruher Pyramide schätzen|[[Datei:Pyramide am Marktplatz, Karlsruhe.JPG|mini|Karlsruher Pyramide]] | |||
Auf dem Bild siehst du die Karlsruher Pyramide, die auf dem Marktplatz in Karlsruhe steht. Berechne den Oberflächeninhalt der Pyramide (inklusive der Grundfläche), indem du zuvor die für die Berechnung notwendigen Größen schätzt. | |||
{{Box | {{Box | ||
| Zeile 261: | Zeile 377: | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
Es gilt <math>h_a=7,45 \text{ m} </math> und <math>a=6,05 \text{ m.} </math> | Es gilt <math>h_a=7{,}45 \text{ m} </math> und <math>a=6{,}05 \text{ m.} </math> | ||
Damit gilt dann: | |||
'''Grundfläche G:''' | |||
<math>G=a^{2}=6{,}05^{2}</math> | |||
<math>G=36{,}6 \text{ m}^{2}</math> | |||
'''Seitenfläche A:''' | |||
<math>A=\frac{a\cdot h_a}{2}=\frac{6{,}05\cdot 7{,}45}{2} </math> | |||
<math>A=22{,}54 \text{ m}^{2} </math> | |||
<math> | '''Mantelfläche M:''' | ||
<math>M = 4 \cdot A = 4\cdot 22{,}54</math> | |||
<math>M = 90{,}16 \text{ m}^{2} </math> | |||
'''Oberfläche O:''' | |||
<math>O = G + M = 36{,}6 + 90{,}16 </math> | |||
<math>O = 126{,}76 \text{ m}^{2}</math> | |||
|Lösung|Lösung verbergen}} | |Lösung|Lösung verbergen}} | ||
|Arbeitsmethode |Farbe=#CD2990}} | |Arbeitsmethode |Farbe=#CD2990}} | ||
==Vertiefen und Vernetzen== | ==Vertiefen und Vernetzen== | ||
{{Box|Info|In diesem Abschnitt findest du vertiefende Aufgaben zu dem Oberflächeninhalt von Pyramiden und darüber hinausgehenden Themen. Neben Pyramiden kommen in diesem Abschnitt auch weitere Körper bzw. Flächen vor, die du zum Teil bereits aus dem Unterricht kennst. Die Aufgabe | {{Box|Info|In diesem Abschnitt findest du vertiefende Aufgaben zu dem Oberflächeninhalt von Pyramiden und darüber hinausgehenden Themen. Neben Pyramiden kommen in diesem Abschnitt auch weitere Körper bzw. Flächen vor, die du zum Teil bereits aus dem Unterricht kennst. Die Aufgabe 13 ist als Knobelaufgabe gedacht, sodass du hier testen kannst, wie fit du im Umgang mit den Oberflächeninhalten von Pyramiden und ähnlichen Körpern bist.|Kurzinfo}} | ||
{{Box| | {{Box|Aufgabe 12: Nikolaus-Häuschen| | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] ''' | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
{{Lösung versteckt|Die Dachfläche besteht aus vier Dreiecken, von denen die jeweils gegenüberliegenden gleich groß sind.|Tipp|Tipp verbergen}} | {{Lösung versteckt|Die Dachfläche besteht aus vier Dreiecken, von denen die jeweils gegenüberliegenden gleich groß sind.|Tipp|Tipp verbergen}} | ||
{{Lösung versteckt|Wir berechnen als erstes den Oberflächeninhalt des Quaders. Die Grundfläche berechnet sich aus | {{Lösung versteckt|Wir berechnen als erstes den Oberflächeninhalt des Quaders. Die Grundfläche berechnet sich aus | ||
<math>G=a \cdot b=6 \cdot 12=72 \text{ cm}^{ | <math>G=a \cdot b=6 \cdot 12=72 \text{ cm}^{2}</math>. | ||
Als nächstes wird die Mantelfläche des Quaders berechnet. | Als nächstes wird die Mantelfläche des Quaders berechnet. | ||
| Zeile 308: | Zeile 443: | ||
{{Box| | {{Box|Aufgabe 13: Tipi| | ||
[[Datei:Teepee and Clifford King (14059271679).jpg|mini|alternativtext=|Tipi]] | [[Datei:Teepee and Clifford King (14059271679).jpg|mini|alternativtext=|Tipi]] | ||
Aktuelle Version vom 1. Dezember 2022, 07:53 Uhr
Wiederholung
Rechteckigen Flächeninhalt berechnen
Dreieckigen Flächeninhalt berechnen
Oberflächeninhalte berechnen
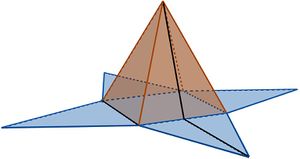
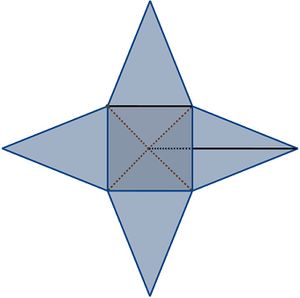
Wie du bereits im vorherigen Kapitel entdeckt hast, lässt sich die Oberfläche einer Pyramide in ein Netz überführen, indem man die Pyramide aufklappt und die Seitenflächen auf eine Ebene faltet.
Das so entstandene Netz besteht somit aus einer Grundfläche und den dreieckigen Seitenflächen, welche zusammen die sogenannte Mantelfläche bilden.
Den Flächeninhalt des gesamten Netzes nennt man den Oberflächeninhalt . Du kannst dir diese Größe als Menge an Verpackung vorstellen, die du benötigst, um das pyramidenförmige Objekt zu umschließen.
Im Falle einer quadratischen Pyramide, welche ihre Spitze über der Mitte ihrer Grundfläche hat, ergibt sich für die Grundfläche die Fläche eines Quadrates und für ihre Mantelfläche die Flächeninhalte von vier gleich großen Dreiecken.
Pyramiden schätzen
Vertiefen und Vernetzen