Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden verknüpfen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (47 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box | {{Box | ||
|1=Info | |1=Info | ||
| Zeile 17: | Zeile 15: | ||
===Checkliste - Das brauchst du=== | ===Checkliste - Das brauchst du=== | ||
{{Box|1=Checkliste|2= | {{Box|1=Checkliste|2= | ||
Für dieses Kapitel solltest du... | Für dieses Kapitel solltest du... | ||
* die Oberfläche einer Pyramide berechnen können (siehe Kapitel [[Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden vermessen]]). | * die Oberfläche einer Pyramide berechnen können (siehe Kapitel [[Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden vermessen|Pyramiden vermessen]]). | ||
* den Satz des Pythagoras anwenden können. | * den Satz des Pythagoras anwenden können. | ||
|3=Hervorhebung1}} | |3=Hervorhebung1}} | ||
{{Box | {{Box | ||
|1=Info | |1=Info | ||
|2= Falls du den Satz des Pythagoras noch einmal wiederholen möchtest, kannst du dein Wissen in Aufgabe 1 auffrischen. | |2= Falls du den Satz des Pythagoras noch einmal wiederholen möchtest, kannst du dein Wissen in Aufgabe 1 auffrischen. Wenn du dich schon sicher im Umgang mit dem Satz des Pythagoras fühlst, kannst du direkt mit Aufgabe 2 fortfahren. | ||
Wenn du dich schon sicher im Umgang mit dem Satz des Pythagoras fühlst, kannst du direkt mit Aufgabe 2 fortfahren. | |||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
===Satz des Pythagoras=== | ===Satz des Pythagoras=== | ||
{{Box|Aufgabe 1: Wiederholung des Satzes von Pythagoras| | {{Box|Aufgabe 1: Wiederholung des Satzes von Pythagoras| | ||
'''a)''' Ergänze den Lückentext mit den bereits bekannten Begriffen des Satzes von Pythagoras. | |||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Klicke zum Ausfüllen auf die Lücken und wähle aus den angegebenen Vorschlägen aus. Kontrolliere deine Lösung mit dem blauen Haken. | |||
[[Datei:About icon (The Noun Project).svg|15px|middle]] | |||
Klicke zum Ausfüllen auf die Lücken und wähle aus den angegebenen Vorschlägen aus. Kontrolliere deine Lösung mit dem blauen Haken. | |||
{{LearningApp|width=100%|height=300px|app=p5zieoapa22}} | {{LearningApp|width=100%|height=300px|app=p5zieoapa22}} | ||
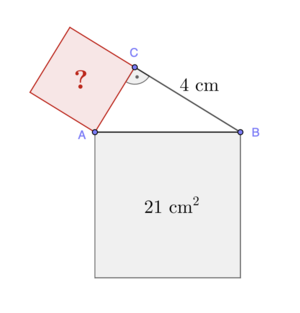
'''b)''' Berechne den Flächeninhalt des roten Quadrats. | |||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]]'''zurück zum Arbeitsblatt''' | |||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] | |||
[[Datei:Flächenberechnung im rechtwinkligen Dreieck.png|zentriert|rahmenlos]] | [[Datei:Flächenberechnung im rechtwinkligen Dreieck.png|zentriert|rahmenlos]] | ||
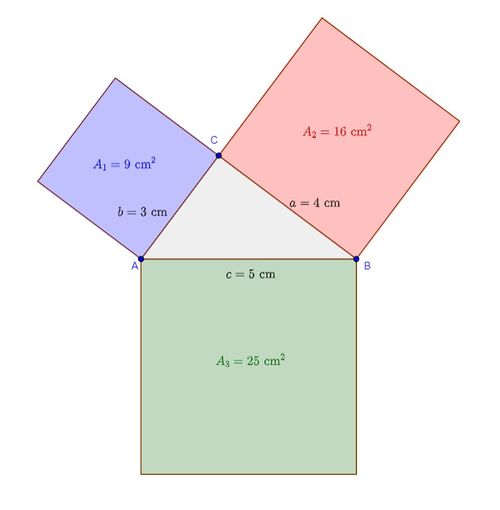
{{Lösung versteckt|1= Schau dir die Abbildung an. Kannst du die Abbildung auf die Aufgabe beziehen? | {{Lösung versteckt|1=Schau dir die Abbildung an. Kannst du die Abbildung auf die Aufgabe beziehen? | ||
[[Datei:Satz des Pythagoras.jpg|zentriert |rahmenlos |500px]] In diesem Beispiel gilt: <math>4^2 + 3^2 = 5^2</math>.|2= Tipp 1 zu b) anzeigen|3= Tipp 1 zu b) verbergen}} | [[Datei:Satz des Pythagoras.jpg|zentriert |rahmenlos |500px]] In diesem Beispiel gilt: <math>4^2 + 3^2 = 5^2</math>.|2= Tipp 1 zu b) anzeigen|3= Tipp 1 zu b) verbergen}} | ||
| Zeile 66: | Zeile 51: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math>\begin{align} | <math>\begin{align} | ||
& & (4 \text{ cm})^2 + b^2 &= 21\text{ cm}^2 | & & (4 \text{ cm})^2 + b^2 &= 21 \text{ cm}^2 & &\mid - (4 \text{ cm})^2\\ | ||
\Leftrightarrow & & | \Leftrightarrow & & b^2 &= 21 \text{ cm}^2 - (4 \text{ cm})^2 \\ | ||
\Leftrightarrow & & | \Leftrightarrow & & b^2 &= 21 \text{ cm}^2 - 16 \text{ cm}^2 \\ | ||
\Leftrightarrow & & | \Leftrightarrow & & b^2 &= 5 \text{ cm}^2 | ||
\end{align}</math> | \end{align}</math> | ||
Der Flächeninhalt des roten Quadrats beträgt <math>5 \text{ cm}^2</math>. | Der Flächeninhalt des roten Quadrats beträgt <math>5 \text{ cm}^2</math>. | ||
|2=Lösung zu b) anzeigen|3=Lösung zu b) verbergen}} | |2=Lösung zu b) anzeigen|3=Lösung zu b) verbergen}} | ||
|Arbeitsmethode | Farbe={{Farbe|orange}}}} | |Arbeitsmethode | Farbe={{Farbe|orange}}}} | ||
===Anwendungsaufgaben=== | ===Anwendungsaufgaben=== | ||
{{Box | {{Box | ||
|Aufgabe 2: Sightseeing in Paris 1 - Der Louvre | |Aufgabe 2: Sightseeing in Paris 1 - Der Louvre | ||
|[[Datei:Grundlagen-bearbeiten.png|30px|middle]] | |[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
Du machst mit deiner Familie Urlaub in Paris und besichtigst einige Sehenswürdigkeiten. Zuerst nehmt ihr an einer Führung durch das berühmte Museum ''Louvre'' teil. Das nebenstehende Bild zeigt die im Innenhof des Louvre stehende Glaspyramide mit quadratischer Grundfläche. | [[Datei:Parigi - Pyramide du Louvre - panoramio.jpg|mini|Glaspyramide im Innenhof des Louvre.]] Du machst mit deiner Familie Urlaub in Paris und besichtigst einige Sehenswürdigkeiten. Zuerst nehmt ihr an einer Führung durch das berühmte Museum ''Louvre'' teil. Das nebenstehende Bild zeigt die im Innenhof des Louvre stehende Glaspyramide mit quadratischer Grundfläche. | ||
Während eurer Führung durch das Museum stellt eine Touristin folgende Frage: | Während eurer Führung durch das Museum stellt eine Touristin folgende Frage: "Wie lang sind die Edelstahlträger an den Seitenkanten der Pyramide?" Der Touristenführer weiß nur, dass die Pyramide 21 Meter hoch ist. | ||
'''a)''' Beurteile, ob diese Angabe genügt, um die Länge eines Stahlträgers zu berechnen. Falls dem nicht so ist, gib Größen an, die zusätzlich benötigt werden. | '''a)''' Beurteile, ob diese Angabe genügt, um die Länge eines Stahlträgers zu berechnen. Falls dem nicht so ist, gib Größen an, die zusätzlich benötigt werden. | ||
| Zeile 99: | Zeile 78: | ||
{{Lösung versteckt|1=Überlege dir Hilfsdreiecke innerhalb der Pyramide, in denen du den Satz des Pythagoras anwenden kannst.|2= Tipp 3 zu b) anzeigen|3=Tipp 3 zu b) verbergen}} | {{Lösung versteckt|1=Überlege dir Hilfsdreiecke innerhalb der Pyramide, in denen du den Satz des Pythagoras anwenden kannst.|2= Tipp 3 zu b) anzeigen|3=Tipp 3 zu b) verbergen}} | ||
{{Lösung versteckt|1=Im nachstehenden GeoGebra-Applet kannst du dir durch das Anklicken der einzelnen Boxen mögliche Hilfsdreiecke anzeigen lassen. | {{Lösung versteckt|1=Im nachstehenden GeoGebra-Applet kannst du dir durch das Anklicken der einzelnen Boxen mögliche Hilfsdreiecke anzeigen lassen. | ||
<div style="width:calc(100%-1rem);height:0;padding-bottom: | <div style="width:calc(100% - 1rem); height:0; padding-bottom:51%;"><ggb_applet id="kqmcb8yu" width="2560" height="1300" sdz="false" /></div> | ||
|2=Tipp 4 zu b) anzeigen|3=Tipp 4 zu b) verbergen}} | |||
{{Lösung versteckt|1= Gegeben sind die Höhe der Pyramide mit <math>h=21~\mathrm{m}</math> und die Seitenlänge der Grundfläche mit <math>a=35~\mathrm{m}</math>. | |||
Du kannst verschiedene Kombinationen an Hilfsdreiecken nutzen, um die Länge eines Stahlträgers zu bestimmen. | |||
Im Folgenden zeigen wir eine dieser Möglichkeiten. | Im Folgenden zeigen wir eine dieser Möglichkeiten. | ||
| Zeile 109: | Zeile 91: | ||
\begin{align} | \begin{align} | ||
& & (35~\mathrm{m})^2+ (35~\mathrm{m})^2 &=d_a^2 & &\mid \text{Termumformung}\\ | & & (35~\mathrm{m})^2+ (35~\mathrm{m})^2 &=d_a^2 & &\mid \text{Termumformung}\\ | ||
\Leftrightarrow & & 2450~\mathrm{m}^2 &=d_a^2 | \Leftrightarrow & & 2450~\mathrm{m}^2 &=d_a^2 & &\mid \sqrt{} \\ | ||
\Leftrightarrow & & | \Leftrightarrow & & \sqrt{2450~\mathrm{m}^2} &=d_a & &\mid \text{Termumformung}\\ | ||
\Leftrightarrow & & | \Leftrightarrow & & 49{,}50~\mathrm{m} &\approx d_a & & | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Zeile 119: | Zeile 101: | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
& & | & & \left(\frac{d_a}{2}\right)^2+ h^2 &=s^2 & &\mid \sqrt{}\\ | ||
\Leftrightarrow & & \sqrt{\left(\frac{d_a}{2}\right)^2+ h^2} &=s | \Leftrightarrow & & \sqrt{\left(\frac{d_a}{2}\right)^2+ h^2} &=s & &\mid \text{Werte einsetzen} \\ | ||
\Leftrightarrow & & | \Leftrightarrow & & \sqrt{\left(\frac{49{,}50~\text{m}}{2}\right)^2+ (21~\text{m})^2} &=s & &\mid \text{Termumformung}\\ | ||
\Leftrightarrow & & | \Leftrightarrow & & 32{,}46~\mathrm{m} &\approx s & & | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Zeile 129: | Zeile 111: | ||
'''c)''' Ebenfalls kam die Frage auf, wie viele Quadratmeter Glasfläche die Reinigungsfirma von außen putzen muss. Beantworte die Frage durch mathematische Rechnungen. | '''c)''' Ebenfalls kam die Frage auf, wie viele Quadratmeter Glasfläche die Reinigungsfirma von außen putzen muss. Beantworte die Frage durch mathematische Rechnungen. | ||
{{Lösung versteckt|1=Die Größe der Glasfläche entspricht der Mantelfläche der Pyramide.|2=Tipp 1 zu c) anzeigen|3=Tipp 1 zu c) verbergen}} | |||
{{Lösung versteckt|1=Verwende die berechnete Länge eines Stahlträgers aus Aufgabenteil b) und bestimme damit in einem geeigneten Hilfsdreieck die Seitenhöhe der Pyramide.|2=Tipp 2 zu c) anzeigen|3=Tipp 2 zu c) verbergen}} | {{Lösung versteckt|1=Verwende die berechnete Länge eines Stahlträgers aus Aufgabenteil b) und bestimme damit in einem geeigneten Hilfsdreieck die Seitenhöhe der Pyramide.|2=Tipp 2 zu c) anzeigen|3=Tipp 2 zu c) verbergen}} | ||
{{Lösung versteckt|1=Im nachstehenden GeoGebra-Applet kannst du dir durch das Anklicken der einzelnen Boxen verschiedene Hilfsdreiecke in der Pyramide anzeigen lassen. Suche das geeignete Hilfsdreieck, um die Seitenhöhe zu berechnen. | |||
<div style="width:calc(100% - 1rem); height:0; padding-bottom:51%;"><ggb_applet id="kqmcb8yu" width="2560" height="1300" sdz="false" /></div> | |||
|2=Tipp 3 zu c) anzeigen|3=Tipp 3 zu c) verbergen}} | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Es wird der Satz des Pythagroas auf das Dreieck, welches aus einer Seitenkante <math> s \approx 32{,}46~\mathrm{m}</math> der Pyramide, der Höhe der Pyramidenseite <math> h_a </math> und der Hälfte der Seitenlänge der Grundfläche <math> \frac{a}{2} = \frac{35~\mathrm{m}}{2} </math> besteht, angewendet. | |||
Damit folgt für die Höhe der Pyramidenseite <math> h_a </math>: | Damit folgt für die Höhe der Pyramidenseite <math> h_a </math>: | ||
| Zeile 143: | Zeile 129: | ||
\begin{align} | \begin{align} | ||
& & h_a^2+ \left(\frac{35~\mathrm{m}}{2}\right)^2 &= s^2 & & \mid -\left(\frac{35~\mathrm{m}}{2}\right)^2 \\ | & & h_a^2+ \left(\frac{35~\mathrm{m}}{2}\right)^2 &= s^2 & & \mid -\left(\frac{35~\mathrm{m}}{2}\right)^2 \\ | ||
\Leftrightarrow & & h_a^2 &= s - \left(\frac{35~\mathrm{m}}{2}\right)^2 & &\mid \sqrt{} | \Leftrightarrow & & h_a^2 &= s - \left(\frac{35~\mathrm{m}}{2}\right)^2 & &\mid \sqrt{}\\ | ||
\Leftrightarrow & & h_a &= \sqrt{ s^2 - \left(\frac{35~\mathrm{m}}{2}\right)^2} & & \mid \text{Werte einsetzen} \\ | \Leftrightarrow & & h_a &= \sqrt{ s^2 - \left(\frac{35~\mathrm{m}}{2}\right)^2} & & \mid \text{Werte einsetzen} \\ | ||
\Leftrightarrow & & h_a &\approx \sqrt{ (32{,}46~\mathrm{m})^2 - (17{,}5~\mathrm{m})^2} & & \mid \text{Termumformung}\\ | \Leftrightarrow & & h_a &\approx \sqrt{ (32{,}46~\mathrm{m})^2 - (17{,}5~\mathrm{m})^2} & & \mid \text{Termumformung}\\ | ||
| Zeile 159: | Zeile 145: | ||
</math> | </math> | ||
Die gesamte Glasfläche der Pyramide <math> M </math> | Die gesamte Glasfläche der Pyramide <math> M </math> besteht aus vier identischen Glaswandflächen <math> A_\text{Seitenfläche} \approx 478{,}45~\mathrm{m}^2</math>: | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| Zeile 168: | Zeile 154: | ||
</math> | </math> | ||
Damit besitzt eine Glaswand eine Fläche von etwa | Damit besitzt eine Glaswand eine Fläche von etwa <math>478{,}45~\mathrm{m}^2 </math>. Die gesamte Glasfläche der Pyramide beträgt demnach rund <math> 1913{,}8~\mathrm{m}^2 </math>. |2=Lösung zu c) anzeigen|3=Lösung zu c) verbergen}} | ||
'''d)''' Vergleiche deine Vorgehensweise in den Aufgabenteilen b) und c) hinsichtlich gemeinsamer Teilschritte | '''d)''' Vergleiche deine Vorgehensweise in den Aufgabenteilen b) und c) hinsichtlich gemeinsamer Teilschritte. Markiere und benenne diese in deinen Aufzeichnungen. | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
{{Box|1=|Aufgabe 3: Checkliste zur Bestimmung der Mantelfläche|2= | |||
{{Box|1=Checkliste zur Bestimmung der Mantelfläche|2= | |||
In Aufgabe 2 hast du bereits eine Möglichkeit zur Bestimmung der Mantelfläche einer Pyramide erkundet und in Aufgabenteil 2d) auch schon angefangen, die dazu nötige Vorgehensweise zu beschreiben. | In Aufgabe 2 hast du bereits eine Möglichkeit zur Bestimmung der Mantelfläche einer Pyramide erkundet und in Aufgabenteil 2d) auch schon angefangen, die dazu nötige Vorgehensweise zu beschreiben. | ||
'''a)''' In dem folgenden Applet wird die allgemeine Vorgehensweise noch einmal zusammengefasst. Bringe die einzelnen Teilschritte in die richtige Reihenfolge. | '''a)''' In dem folgenden Applet wird die allgemeine Vorgehensweise noch einmal zusammengefasst. Bringe die einzelnen Teilschritte in die richtige Reihenfolge. | ||
{{LearningApp|width=100%|height=500px|app=p74tsoa4c22}} | {{LearningApp|width=100%|height=500px|app=p74tsoa4c22}} | ||
'''b)''' [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | '''b)''' [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
Übertrage die Checkliste auf das Arbeitsblatt | Übertrage die Checkliste auf das Arbeitsblatt "Pyramiden verknüpfen". | ||
|3=Arbeitsmethode}} | |||
|3= | |||
{{Box | {{Box | ||
|Aufgabe | |1=Aufgabe 4 ⭐: Sightseeing in Paris 2 - Der Eiffelturm | ||
|[[Datei:Grundlagen-bearbeiten.png|30px|middle]] | |2=[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
[[Datei:Tour Eiffel Wikimedia Commons.jpg|120px|mini|Eiffelturm]] | [[Datei:Tour Eiffel Wikimedia Commons.jpg|120px|mini|Eiffelturm]] | ||
| Zeile 198: | Zeile 179: | ||
Als nächster Stopp steht der Eiffelturm auf eurer Liste. | Als nächster Stopp steht der Eiffelturm auf eurer Liste. | ||
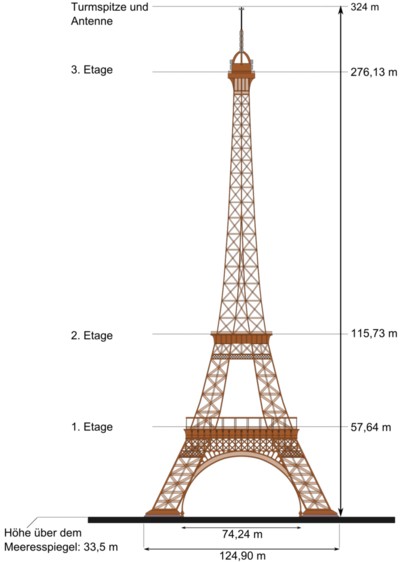
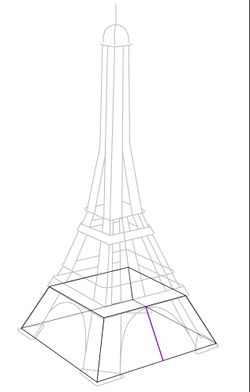
Das Gerüst des Eiffelturms wird momentan erneuert. Damit es für die Touristen trotzdem attraktiv bleibt, ist der untere Teil bis zur ersten Etage von einem Banner bedeckt, welches den renovierten Eiffelturm darstellen soll. Du möchtest gerne wissen, wie viel Stoff für das Banner benötigt wird. Dazu entnimmst du einer Informationstafel am Eiffelturm einige wichtige Maße des Bauwerks und bemerkst dabei, dass dir noch Daten zur Berechnung fehlen. Zunächst nimmst du an, dass die erste Etage um die Breite eines Fußes eingerückt ist. Berechne näherungsweise die Stoffmenge des Banners und triff gegebenenfalls weitere Annahmen. | |||
[[Datei:Eiffelturm mit technischen Daten.png|zentriert | rahmenlos | 400px | thumb]] | |||
{{Lösung versteckt|1= Schätze anhand der obigen Skizze des Eiffelturms die Breite der 1. Etage. | |||
|2=Tipp 1 anzeigen |3= Tipp 1 verbergen}} | |||
{{Lösung versteckt|1= Kannst du im Eiffelturm eine Pyramide entdecken? | |||
|2=Tipp 2 anzeigen |3= Tipp 2 verbergen}} | |||
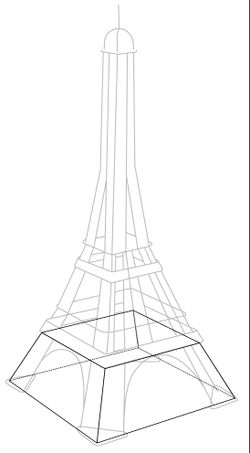
{{Lösung versteckt|1= Der Eiffelturm besitzt bis zur 1. Etage die Form eines Pyramidenstumpfes. Den Pyramidenstumpf kannst du der unten stehenden Skizze entnehmen. Überlege dir anhand der Skizze welche Größen du schon kennst und welche Größen du noch bestimmen musst. | |||
[[Datei:Eiffelturm mit Pyramidenstumpf.jpg| zentriert | rahmenlos | 250px | thumb]] | |||
|2=Tipp 3 anzeigen |3= Tipp 3 verbergen}} | |||
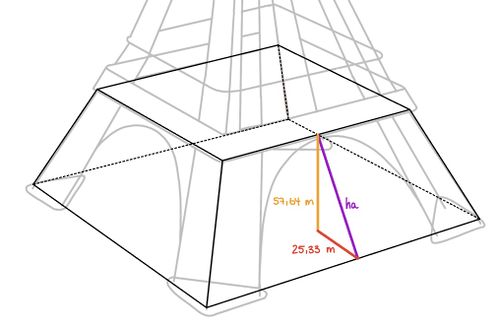
{{Lösung versteckt|1= Zur Berechnung des Flächeninhalts eines Trapezes benötigst du die Seitenhöhe des Pyramidenstumpfes. Die Seitenhöhe entspricht der lila Strecke in der unterstehenden Skizze. Konstruiere ein passendes Hilfsdreieck und wende den Satz des Pythagoras an. | |||
[[Datei:Eiffelturm mit Stütze und Pyramidenstumpf.jpg| zentriert | rahmenlos | 250px | thumb]] | |||
|2=Tipp 4 anzeigen |3= Tipp 4 verbergen}} | |||
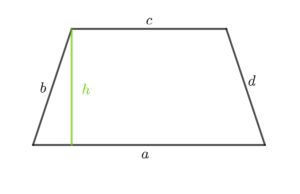
{{Lösung versteckt|1= Der Flächeninhalt <math>A_T</math> eines Trapezes wird über die folgende Formel berechnet: | |||
<math>A_T= \frac{1}{2} (a+c) \cdot h</math>. | |||
[[Datei:Trapez mit Höhe.png|zentriert | rahmenlos | 300px | thumb]] | |||
|2=Tipp 5 anzeigen |3= Tipp 5 verbergen}} | |||
{{Lösung versteckt|1= | |||
[[Datei:Eiffelturm mit Pyramidenstumpf und Hilfsdreieck.jpg|zentriert | rahmenlos | 500px | thumb]] | |||
Die Breite der ersten Etage kann anhand der Breite des Torbogens auf <math>74{,}24 ~\text{m}</math> geschätzt werden. Die <span style="color:darkred">'''Länge eines Fußes'''</span> des Eiffelturms wird über die folgende Gleichung bestimmt: | |||
<math>l_\text{Fuß} = \frac{124{,}90 ~\text{m} - 74{,}24 ~\text{m}}{2} = 25{,}33 ~\text{m}</math>. | |||
Die Seitenhöhe <math>h_a</math> des Trapezes wird über den Satz des Pythagoras bestimmt. Es gilt: | |||
<math>\begin{align} | |||
& & h_a^2&=(57{,}64 ~\text{m})^2 + (25{,}33 ~\text{m})^2 & &\mid \sqrt{} \\ | |||
\Leftrightarrow & & h_a&=\sqrt{(57{,}64 ~\text{m})^2 + (25{,}33 ~\text{m})^2} \\ | |||
\Leftrightarrow & & h_a &\approx 62{,}96 ~\text{m} \\ | |||
\end{align}</math> | |||
Nun kann der Flächeninhalt <math>A_T</math> des Trapezes berechnet werden: | |||
<math>\begin{align} | |||
A_T &= \frac{1}{2} (74{,}24 ~\text{m} + 124{,}90 ~\text{m})\cdot 62{,}96 ~\text{m} \\ | |||
&\approx 6268{,}93 ~\text{m}^2 \\ | |||
\end{align}</math> | |||
Der Flächeninhalt der vier Trapeze entspricht somit: | |||
{{ | <math>\begin{align} | ||
A_{\text{Banner}} &= 4 \cdot A_T \\ | |||
&=4 \cdot 6268{,}93 ~\text{m}^2 \\ | |||
&= 25075{,}72 ~\text{m}^2 \\ | |||
\end{align}</math> | |||
Die benötigte Fläche der vier Banner beträgt somit <math>A_{\text{Banner}} = 25075{,}72 ~\text{m}^2</math>. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| 3=Arbeitsmethode}} | | 3=Arbeitsmethode}} | ||
{{Box | {{Box | ||
|Aufgabe | |1=Aufgabe 5 ⭐: Der Würfel | ||
|[[Datei:Grundlagen-bearbeiten.png|30px|middle]] | |2=[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
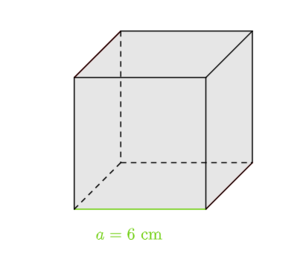
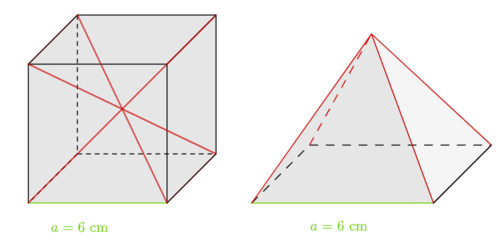
Der unten abgebildete Würfel lässt sich aus 6 regelmäßigen, gleichartigen Pyramiden zusammensetzen. | Der unten abgebildete Würfel lässt sich aus 6 regelmäßigen, gleichartigen Pyramiden zusammensetzen. | ||
| Zeile 224: | Zeile 245: | ||
[[Datei:Würfel Seitenlänge 6 cm.png|zentriert | rahmenlos| 300px | thumb]] | [[Datei:Würfel Seitenlänge 6 cm.png|zentriert | rahmenlos| 300px | thumb]] | ||
'''a)''' Beschreibe wie sich der Würfel aus den Pyramiden zusammensetzen lässt und wie diese Pyramiden aussehen. | |||
{{Lösung versteckt|1= Überlege dir eine naheliegende Form für die Grundfläche der Pyramiden. |2=Tipp 1 zu a) anzeigen|3=Tipp 1 a) verbergen}} | {{Lösung versteckt|1= Überlege dir eine naheliegende Form für die Grundfläche der Pyramiden. |2=Tipp 1 zu a) anzeigen|3=Tipp 1 a) verbergen}} | ||
| Zeile 234: | Zeile 255: | ||
Kannst du dir nun besser vorstellen, wie die gesuchte Pyramide aussieht? | Kannst du dir nun besser vorstellen, wie die gesuchte Pyramide aussieht? | ||
<div style="width:calc(100% - 1rem); height:0; padding-bottom:50%;"><ggb_applet id="utuufrpf" width=" | <div style="width:calc(100% - 1rem); height:0; padding-bottom:50%;"><ggb_applet id="utuufrpf" width="1000" height="500"/></div> | ||
|2=Tipp 3 zu a) anzeigen|3= Tipp 3 zu a) verbergen}} | |2=Tipp 3 zu a) anzeigen|3= Tipp 3 zu a) verbergen}} | ||
| Zeile 246: | Zeile 266: | ||
Die Pyramiden besitzen eine quadratische Grundfläche mit einer Seitenlänge von 6 cm und sind symmetrisch. | Die Pyramiden besitzen eine quadratische Grundfläche mit einer Seitenlänge von 6 cm und sind symmetrisch. | ||
Der Würfel lässt sich aus 6 solchen Pyramiden zusammensetzen, indem die Seitenflächen des Würfels die Grundflächen der Pyramiden darstellen. Die Spitzen der 6 Pyramiden treffen sich im Mittelpunkt des Würfels. | Der Würfel lässt sich aus 6 solchen Pyramiden zusammensetzen, indem die Seitenflächen des Würfels die Grundflächen der Pyramiden darstellen. Die Spitzen der 6 Pyramiden treffen sich im Mittelpunkt des Würfels. | ||
|2=Lösung zu a) anzeigen|3=Lösung zu a) verbergen}} | |2=Lösung zu a) anzeigen|3=Lösung zu a) verbergen}} | ||
'''b)''' Welche Höhe hat die Pyramide? | |||
{{Lösung versteckt|1= Sieh dir noch einmal den Tipp 3 in Teilaufgabe a) ganz genau an. |2=Tipp 1 zu b) anzeigen|3= Tipp 1 zu b) verbergen}} | {{Lösung versteckt|1= Sieh dir noch einmal den Tipp 3 in Teilaufgabe a) ganz genau an. |2=Tipp 1 zu b) anzeigen|3= Tipp 1 zu b) verbergen}} | ||
| Zeile 256: | Zeile 274: | ||
{{Lösung versteckt|1= Die Spitzen der Pyramiden treffen sich im Mittelpunkt des Würfels. Somit sind zwei Pyramiden, die aufeinander stehen, genauso hoch wie der Würfel (<math>6~\text{cm}</math>). Daraus ergibt sich, dass die Pyramiden eine Höhe von <math>3~\text{cm}</math> haben. |2=Lösung zu b) anzeigen|3=Lösung zu b) verbergen}} | {{Lösung versteckt|1= Die Spitzen der Pyramiden treffen sich im Mittelpunkt des Würfels. Somit sind zwei Pyramiden, die aufeinander stehen, genauso hoch wie der Würfel (<math>6~\text{cm}</math>). Daraus ergibt sich, dass die Pyramiden eine Höhe von <math>3~\text{cm}</math> haben. |2=Lösung zu b) anzeigen|3=Lösung zu b) verbergen}} | ||
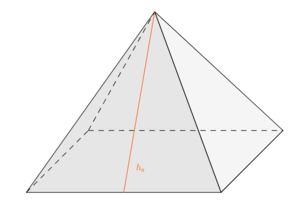
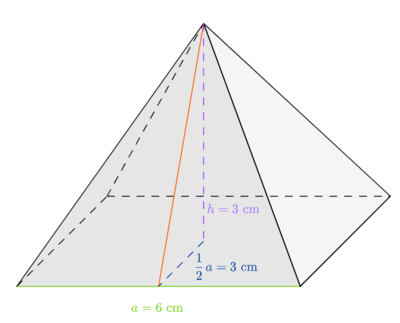
'''c)''' Berechne die Länge der orange markierten Strecke <math> h_a </math>. Runde dabei auf 2 Nachkommastellen genau. | |||
[[Datei:Pyramide mit Seitenhöhe.png|zentriert | rahmenlos | 300px | thumb]] | [[Datei:Pyramide mit Seitenhöhe.png|zentriert | rahmenlos | 300px | thumb]] | ||
| Zeile 270: | Zeile 287: | ||
Mit Hilfe des Satzes des Pythagoras ergibt sich die folgende Formel: | Mit Hilfe des Satzes des Pythagoras ergibt sich die folgende Formel: | ||
<math> (h_a)^2=h^2+\biggl(\frac{1}{2}\cdot a\biggr)^2 </math>. | <math> (h_a)^{2}=h^2+\biggl(\frac{1}{2}\cdot a\biggr)^2 </math>. | ||
Setzen wir nun, die uns bekannten Werte für <math> h </math> und <math> a </math> ein, so erhalten wir: | Setzen wir nun, die uns bekannten Werte für <math> h </math> und <math> a </math> ein, so erhalten wir: | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
& & | & & h_a^2 &= 3^2 + \left(\frac{1}{2}\cdot 6\right)^2 & & \mid \text{Termumformung}\\ | ||
\Leftrightarrow & & | \Leftrightarrow & & h_a^2 &= 3^2 + 3^2 & &\mid \text{Termumformung}\\ | ||
\Leftrightarrow & & | \Leftrightarrow & & h_a^2 &= 18 & & \mid \sqrt{}\\ | ||
\Leftrightarrow & & | \Leftrightarrow & & h_a &\approx 4{,}24 & & | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Zeile 286: | Zeile 303: | ||
| 3=Arbeitsmethode}} | | 3=Arbeitsmethode}} | ||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Pyramiden entdecken#Kapitelauswahl}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | {{SORTIERUNG:{{SUBPAGENAME}}}} | ||
[[Kategorie:Digitale Werkzeuge in der Schule]] | [[Kategorie:Digitale Werkzeuge in der Schule]] | ||