Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Punkte und Vektoren im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
(Navigation hinzugefügt) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 17: | Zeile 17: | ||
Zum Punkt <math>A(1|2|3) </math> gehört also der Ortsvektor <math>\vec {a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} </math>.|3= Merksatz}} | Zum Punkt <math>A(1|2|3) </math> gehört also der Ortsvektor <math>\vec {a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} </math>.|3= Merksatz}} | ||
==Koordinatensystem== | |||
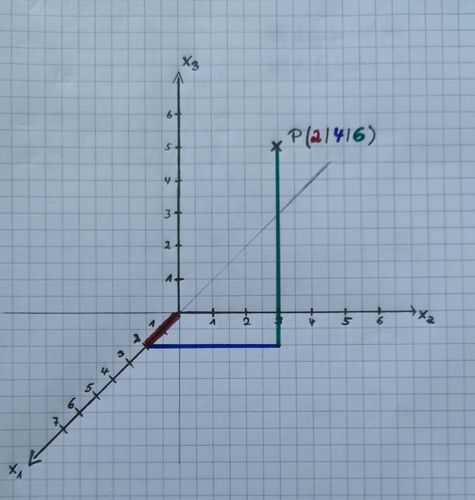
{{Box|1= Aufgabe 1: Koordinatensysteme|2= Für diese Aufgabe benötigst du einen Bleistift, ein kariertes Blatt Papier und ein Geodreieck. Bearbeite die folgenden Aufgaben. | {{Box|1= Aufgabe 1: Koordinatensysteme|2= Für diese Aufgabe benötigst du einen Bleistift, ein kariertes Blatt Papier und ein Geodreieck. Bearbeite die folgenden Aufgaben. | ||
#Zeichne ein dreidimensionales Koordinatensystem. Wähle eine passende Skalierung anhand der angegebenen Punkte im Aufgabenteil 2 und 3. | #Zeichne ein dreidimensionales Koordinatensystem. Wähle eine passende Skalierung anhand der angegebenen Punkte im Aufgabenteil 2 und 3. | ||
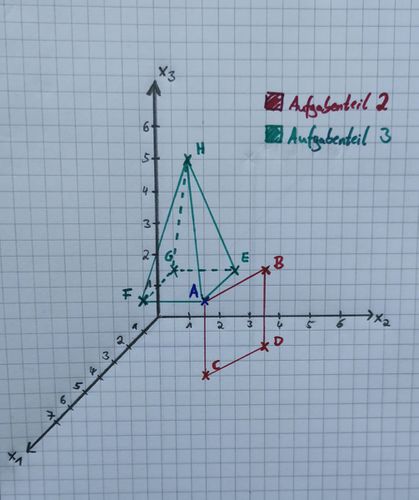
#Zeichne die Punkte <math> A (1|2|1)</math>,<math> B(1|4|2)</math>, <math> C(1|2|{-}1{,}5)</math> und <math> D(1|4|{-}0{,}5) </math> in das gezeichnete Koordinatensystem. Zeichne nun die Verbindungsvektoren <math>\vec{ AB }</math> , <math>\vec{ AC }</math>,<math>\vec{ CD }</math> und <math>\vec{ BD }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | #Zeichne die Punkte <math> A (1|2|1)</math>,<math> B(1|4|2)</math>, <math> C(1|2|{-}1{,}5)</math> und <math> D(1|4|{-}0{,}5) </math> in das gezeichnete Koordinatensystem. Zeichne nun die Verbindungsvektoren <math>\vec{ AB }</math> , <math>\vec{ AC }</math>,<math>\vec{ CD }</math> und <math>\vec{ BD }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | ||
#Nutze den Punkt <math> A (1|2|1)</math> aus Aufgabenteil 2. Füge die Punkte <math> E (-1|2|1)</math>,<math> F(1|0|1)</math>, <math> G(-1|0|1)</math> und <math> H(0|1|5) </math>. Zeichne nun die Verbindungsvektoren <math>\vec{ AE }</math>,<math>\vec{ AF }</math>, <math>\vec{ AH }</math>, <math>\vec{ EG }</math>, <math>\vec{ FG }</math>, <math>\vec{ FH }</math> und <math>\vec{ GH }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | #Nutze den Punkt <math> A (1|2|1)</math> aus Aufgabenteil 2. Füge die Punkte <math> E (-1|2|1)</math>,<math> F(1|0|1)</math>, <math> G(-1|0|1)</math> und <math> H(0|1|5) </math>. Zeichne nun die Verbindungsvektoren <math>\vec{ AE }</math>,<math>\vec{ AF }</math>, <math>\vec{ AH }</math>, <math>\vec{ EG }</math>, <math>\vec{ FG }</math>, <math>\vec{ FH }</math> , <math>\vec{ EH }</math> und <math>\vec{ GH }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | ||
| Zeile 36: | Zeile 37: | ||
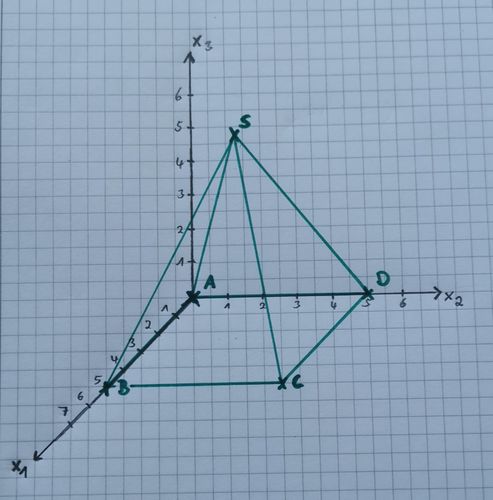
{{Box|1= Aufgabe 2: Geometrische Objekte im Koordinatensystem|2= Die abgebildete Pyramide besitzt einen Eckpunkt im Nullpunkt <math> A(0|0|0)</math>. Die quadratische Grundfläche der Pyramide liegt dabei in der <math> x_1</math>-<math> x_2</math>-Ebene und die Spitze der Pyramide liegt | {{Box|1= Aufgabe 2: Geometrische Objekte im Koordinatensystem|2= Die abgebildete Pyramide besitzt einen Eckpunkt im Nullpunkt <math> A(0|0|0)</math>. Die quadratische Grundfläche der Pyramide liegt dabei in der <math> x_1</math>-<math> x_2</math>-Ebene und die Spitze der Pyramide liegt 6 Längeneinheiten über der Grundfläche. | ||
[[Datei:Pyramide.jpg|rahmenlos|500x500px|Pyramide]] | [[Datei:Pyramide.jpg|rahmenlos|500x500px|Pyramide]] | ||
| Zeile 66: | Zeile 67: | ||
|Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | |Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | ||
==Vektoren als Verschiebungen== | |||
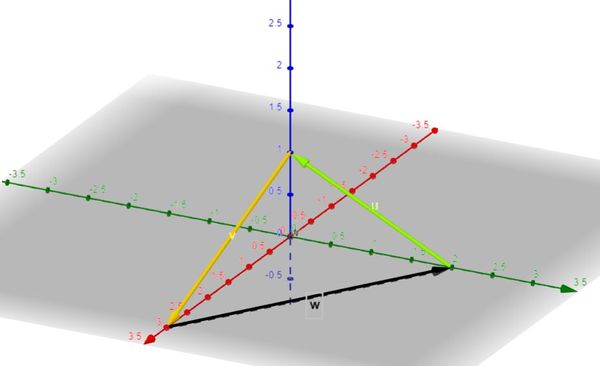
{{Box|1= Aufgabe 3: Verschiebungen durch Vektoren|2= Betrachte die dargestellten Verschiebungen <math>\vec{u} </math> (grün) , <math>\vec{v}</math> (gelb) und <math>\vec{w}</math> (schwarz). Außerdem sind die Punkte <math> A(3|0|0)</math>, <math> B(0|2|0)</math> und <math> C(0|0|1)</math> bekannt. | {{Box|1= Aufgabe 3: Verschiebungen durch Vektoren|2= Betrachte die dargestellten Verschiebungen <math>\vec{u} </math> (grün) , <math>\vec{v}</math> (gelb) und <math>\vec{w}</math> (schwarz). Außerdem sind die Punkte <math> A(3|0|0)</math>, <math> B(0|2|0)</math> und <math> C(0|0|1)</math> bekannt. | ||
[[Datei:Vektoren.jpg|rahmenlos|600x600px]] | [[Datei:Vektoren.jpg|rahmenlos|600x600px]] | ||
Welche Punkte erhältst du bei folgenden Verschiebungen durch die Vektoren? | Welche Punkte erhältst du bei folgenden Verschiebungen durch die Vektoren? | ||
| Zeile 91: | Zeile 91: | ||
|Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | |Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | ||
==Rechnen mit Vektoren== | |||
{{Box|1= Aufgabe 4: Vektoren addieren und mit einem Skalar multiplizieren|2= | {{Box|1= Aufgabe 4: Vektoren addieren und mit einem Skalar multiplizieren|2= | ||
| Zeile 111: | Zeile 111: | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
==Kollinearität von Vektoren== | |||
{{Box|1= Aufgabe 6: Kollinearität von Vektoren|2= | {{Box|1= Aufgabe 6: Kollinearität von Vektoren|2= | ||
| Zeile 117: | Zeile 118: | ||
|3=Arbeitsmethode|Farbe={{Farbe|orange}}}} | |3=Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
==Länge und Abstände von Vektoren== | |||
{{Box|1=Aufgabe 7: Länge und Abstände von Vektoren|2= | {{Box|1=Aufgabe 7: Länge und Abstände von Vektoren|2= | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 155: | Zeile 157: | ||
|3=Arbeitsmethode|Farbe={{Farbe|orange}}}} | |3=Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
==Geometrische Objekte untersuchen== | |||
{{Box|1= Aufgabe 8: Besondere Vierecke | {{Box|1= Aufgabe 8: Besondere Vierecke | ||
|2= | |2= | ||
| Zeile 169: | Zeile 172: | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{b) Wir betrachten weiterhin das Dreieck <math> ABC </math>. Ein neuer Punkt <math> Q </math> soll so gewählt werden, dass er zusammen mit dem Dreieck <math> ABC </math> ein Parallelogramm bildet, das keine Raute ist. Welche Koordinaten passen zu <math> Q </math>? Es sind zwei Antwortmöglichkeiten richtig. Finde beide!} | {b) Wir betrachten weiterhin das Dreieck <math> ABC </math>. Ein neuer Punkt <math> Q </math> soll so gewählt werden, dass er zusammen mit dem Dreieck <math> ABC </math> ein Parallelogramm bildet, das keine Raute ist. Welche Koordinaten passen zu <math> Q </math>? Es sind zwei Antwortmöglichkeiten richtig. Finde beide!} | ||
+ <math> | + <math> Q(6|2|7)</math> | ||
- <math> | - <math> Q(7|4|3)</math> | ||
+ <math> | + <math> Q(0|4|3)</math> | ||
- <math> | - <math> Q(6|3|{-}1)</math> | ||
</quiz> | </quiz> | ||
{{Lösung versteckt|1=Fertige eine Skizze des Dreiecks an und mache dir klar, welche Seite die Basis des Dreiecks ist. |2=Tipp 1|3=Tipp verbergen}} | {{Lösung versteckt|1=Fertige eine Skizze des Dreiecks an und mache dir klar, welche Seite die Basis des Dreiecks ist. |2=Tipp 1|3=Tipp verbergen}} | ||
| Zeile 192: | Zeile 195: | ||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Unterwegs_in_3-D_–_Punkte,_Vektoren,_Geraden_und_Ebenen_im_Raum#Kapitelauswahl}} | {{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Unterwegs_in_3-D_–_Punkte,_Vektoren,_Geraden_und_Ebenen_im_Raum#Kapitelauswahl}} | ||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 24. Juni 2021, 13:39 Uhr
Wiederholung von Punkten und Vektoren
Koordinatensystem
Vektoren als Verschiebungen
Rechnen mit Vektoren