Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Abstände von Objekten im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
(GeoGebra in Klapptext korrigiert) Markierung: Quelltext-Bearbeitung 2017 |
||
| (26 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box | 1=Info | 2= In diesem Lernpfadkapitel kannst du das Thema "Abstände von Objekten im Raum" wiederholen und vertiefen. | {{Box | 1=Info | 2= In diesem Lernpfadkapitel kannst du das Thema "Abstände von Objekten im Raum" wiederholen und vertiefen. | ||
Wie du im Inhaltsverzeichnis siehst, gibt es drei Abschnitte: einen zum Abstand zwischen einer Ebene und einem Punkt, einen zum Abstand zwischen einer Geraden und einem Punkt und einen dritten zum Abstand zwischen zwei windschiefen Geraden. Suche dir einfach aus, was du üben möchtest. Bei jedem Abschnitt werden erst die jeweiligen Verfahren wiederholt und anschließend gibt es ein paar Aufgaben dazu | Wie du im Inhaltsverzeichnis siehst, gibt es drei Abschnitte: einen zum Abstand zwischen einer Ebene und einem Punkt, einen zum Abstand zwischen einer Geraden und einem Punkt und einen dritten zum Abstand zwischen zwei windschiefen Geraden. Suche dir einfach aus, was du üben möchtest. Bei jedem Abschnitt werden erst die jeweiligen Verfahren wiederholt und anschließend gibt es ein paar Aufgaben dazu. Darunter sind auch Knobelaufgaben. | ||
Vorher kannst du noch die Einstiegsaufgabe machen, um deine generelle inhaltliche Vorstellung zu testen. | Vorher kannst du noch die Einstiegsaufgabe machen, um deine generelle inhaltliche Vorstellung zu testen. | ||
| Zeile 25: | Zeile 25: | ||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
Je nachdem, | Im Folgenden werden nun die Verfahren für die verschiedenen Abstandsprobleme wiederholt. | ||
Je nachdem, was du noch üben willst, kannst du dir den jeweiligen Abschnitt dieses Lernpfadkapitels anschauen. | |||
==Abstand eines Punktes von einer Ebene== | ==Abstand eines Punktes von einer Ebene== | ||
| Zeile 59: | Zeile 60: | ||
Den Lotfußpunkt <math>A</math> bestimmen: | Den Lotfußpunkt <math>A</math> bestimmen: | ||
<math> | <math>2(3+2t)+6(4+6t)-4(-2-4t)=-32 | ||
\Rightarrow t=-1,25 </math> | \Rightarrow t=-1,25 </math> | ||
<math>t</math> in <math>l</math> einsetzten: | <math>t</math> in <math>l</math> einsetzten: | ||
<math>\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}-1,25\cdot\begin{pmatrix} 2 \\ 6 \\ -4 \end{pmatrix}=\begin{pmatrix} 0,5 \\ -3,5 \\ 3 \end{pmatrix}</math> | <math>\vec{OA}=\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}-1,25\cdot\begin{pmatrix} 2 \\ 6 \\ -4 \end{pmatrix}=\begin{pmatrix} 0,5 \\ -3,5 \\ 3 \end{pmatrix}</math> | ||
Der Lotfußpunkt ist <math>A(0,5|-3,5|3)</math>. | Der Lotfußpunkt ist <math>A(0,5|-3,5|3)</math>. | ||
| Zeile 79: | Zeile 80: | ||
{{Box | Merke: Formel für den Abstand eines Punktes von einer Ebene| | {{Box | Merke: Formel für den Abstand eines Punktes von einer Ebene mit Hilfe der Hesse´schen Normaleform (HNF)| | ||
Um den Abstand zwischen einem Punkt und einer Ebene zu bestimmen, gibt es neben dem Lotfußpunktverfahren auch die Möglichkeit, diesen mit einer Formel zu berechnen. | Um den Abstand zwischen einem Punkt und einer Ebene zu bestimmen, gibt es neben dem Lotfußpunktverfahren auch die Möglichkeit, diesen mit einer Formel zu berechnen. | ||
| Zeile 107: | Zeile 108: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Abstandsberechnung | Abstandsberechnung des Abstandes eines Punktes von einer Ebene mit der Hesse´schen Normalenform: | ||
| Zeile 135: | Zeile 136: | ||
|2=Lösung mit der | |2=Lösung mit Hilfe der HNF anzeigen|3=Lösung verbergen}} | ||
| Zeile 181: | Zeile 182: | ||
|2=Lösung mit dem Lotfußpunktverfahren anzeigen|3=Lösung verbergen}} | |2=Lösung mit dem Lotfußpunktverfahren anzeigen|3=Lösung verbergen}} | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
| Farbe={{Farbe|orange}} }} | |||
| Zeile 247: | Zeile 242: | ||
Wenn du die Höhe der Pyramide kennst, weißt du, welchen Abstand die Spitze von der Grundfläche hat. Du kennst auch schon den Mittelpunkt der Pyramide und kannst entlang des Normalenvektors von <math>E</math> zur Spitze gelangen. | Wenn du die Höhe der Pyramide kennst, weißt du, welchen Abstand die Spitze von der Grundfläche hat. Du kennst auch schon den Mittelpunkt der Pyramide und kannst entlang des Normalenvektors von <math>E</math> zur Spitze gelangen. | ||
<ggb_applet id="qu6yfdp6" width= | <div style="width:calc(100% - 1rem); height:0; padding-bottom:47%;"><ggb_applet id="qu6yfdp6" width="1000" height="470"/></div>|2=Tipp 2|3=Tipp 2 verbergen}} | ||
|2=Tipp 2|3=Tipp 2 verbergen}} | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| Zeile 284: | Zeile 277: | ||
{{Box | 1=Aufgabe 7: Abstand paralleler Ebenen | 2= Gegeben ist die Ebene <math>E: 2x_1-3x_2+6x_3=13</math>. Bestimme zur Ebene <math>E</math> zwei parallele Ebenen, die von <math>E</math> den Abstand <math>5</math> haben. | {{Box | 1=Aufgabe 7: Abstand paralleler Ebenen | 2= Gegeben ist die Ebene <math>E: 2x_1-3x_2+6x_3=13</math>. Bestimme zur Ebene <math>E</math> zwei parallele Ebenen, die von <math>E</math> den Abstand <math>5 LE</math> haben. | ||
| Zeile 339: | Zeile 332: | ||
<math>G_1</math> und <math>G_2</math> haben nun beide den Abstand <math>5</math> zur Ebene <math>E</math>. | <math>G_1</math> und <math>G_2</math> haben nun beide den Abstand <math>5 LE</math> zur Ebene <math>E</math>. | ||
| Zeile 361: | Zeile 354: | ||
Versuche es zuerst ohne die Hilfslinie. Überprüfe dich dann selbst. | Versuche es zuerst ohne die Hilfslinie. Überprüfe dich dann selbst. | ||
<ggb_applet id="fpr58eab" width=" | <ggb_applet id="fpr58eab" width="1000" height="514" /> | ||
{{Lösung versteckt|1=Der Abstand <math>d(P;Q)</math> ist am kleinsten, wenn <math>\vec{PQ}</math> orthogonal zu <math>g</math> ist. Dies kannst du sehen, wenn du dir die Hilfslinie anzeigen lässt. | {{Lösung versteckt|1=Der Abstand <math>d(P;Q)</math> ist am kleinsten, wenn <math>\vec{PQ}</math> orthogonal zu <math>g</math> ist. Dies kannst du sehen, wenn du dir die Hilfslinie anzeigen lässt. | ||
| Zeile 373: | Zeile 366: | ||
2=Der Abstand eines Punktes <math>P</math> zu einer Geraden <math>g</math> ist der Abstand von <math>P</math> und <math>L</math>, wobei <math>L</math> der Lotfußpunkt von <math>P</math> auf <math>g</math> ist. | 2=Der Abstand eines Punktes <math>P</math> zu einer Geraden <math>g</math> ist der Abstand von <math>P</math> und <math>L</math>, wobei <math>L</math> der Lotfußpunkt von <math>P</math> auf <math>g</math> ist. | ||
Für die Bestimmung des Abstandes <math>d(P,g)= | Für die Bestimmung des Abstandes <math>d(P,g)=|\vec{PL}|</math> gibt es zwei verschiedene Verfahren: | ||
'''Verfahren Hilfsebene''' | '''Verfahren Hilfsebene''' | ||
# Stelle eine Hilfsebene <math>H</math> (in Koordinatenform) auf, die | # Stelle eine Hilfsebene <math>H</math> (in Koordinatenform) auf, die orthogonal zur Geraden <math>g</math> ist und den Punkt <math>P</math> enthält. Dafür kannst du als Normalenvektor den Richtungsvektor von <math>g</math> und als Stützvektor <math>\vec{p} </math> nehmen. | ||
# Bestimme den Schnittpunkt <math>L</math> von <math>g</math> und <math>H</math> durch Einsetzen. | # Bestimme den Schnittpunkt <math>L</math> von <math>g</math> und <math>H</math> durch Einsetzen. | ||
# Berechne den Abstand <math>d(P;g)=d(P; | # Berechne den Abstand <math>d(P;g)=|\vec{PL}|</math>. | ||
{{Lösung versteckt|1= | |||
Wir bestimmen den Abstand zwischen der Geraden <math> g:\vec{x}= \begin{pmatrix} 2 \\ 3 \\ 2 \end{pmatrix}+r\cdot\begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix} </math> und dem Punkt <math>P(1|2|-3) </math>. | |||
1. Hilfsebene <math>H</math> aufstellen, die orthogonal zu <math>g</math> ist und den Punkt <math>P</math> enthält: | |||
Ansatz für die Hilfsebene mit dem Richtungsvektor von <math>g</math> als Normalenvektor: <math>H: 2\cdot x_1+x_2-x_3=b</math>. Einsetzen vom Punkt <math>P</math> liefert <math>b=2\cdot 1+2-(-3)=7</math>, also <math>H: 2\cdot x_1+x_2-x_3=7</math>. | |||
2. Schnittpunkt <math>L</math> von <math>g</math> und <math>H</math> durch Einsetzen bestimmen: | |||
<math>7=2\cdot(2+2r)+(3+r)-(2-r)=5+6t</math>, also <math>r=\frac{1}{3}</math>. | |||
Durch Einsetzen von <math>r</math> in die Geradengleichung von <math>g</math> erhält man den Schnittpunkt <math>L(\frac{8}{3}|\frac{10}{3}|\frac{5}{3})</math>. | |||
3. Abstand berechnen: | |||
<math>d(P;g)=|\vec{PL}|=\sqrt{(\frac{8}{3}-1)^2+(\frac{10}{3}-2)^2+(\frac{5}{3}-(-3))^2}=\frac{\sqrt{237}}{3}\approx 5,1316</math> | |||
|2=Beispiel Verfahren Hilfsebene|3=Beispiel verbergen}} | |||
'''Verfahren Orthogonalität''' | '''Verfahren Orthogonalität''' | ||
# Bestimme einen allgmeinen Verbindungsvektor von <math>P</math> zu einem beliebigen Geradenpunkt <math>L</math> in Abhängigkeit vom Geradenparameter <math>r</math>. | # Bestimme einen allgmeinen Verbindungsvektor von <math>P</math> zu einem beliebigen Geradenpunkt <math>L</math> in Abhängigkeit vom Geradenparameter <math>r</math>. | ||
# Wähle <math>r</math> so, dass der Verbindungsvektor orthogonal zum Richtungsvektor der Geraden <math>g</math> ist. | # Wähle <math>r</math> so, dass der Verbindungsvektor orthogonal zum Richtungsvektor der Geraden <math>g</math> ist. | ||
# Berechne nun den Abstand <math>d(P;g)= | # Berechne nun den Abstand <math>d(P;g)=|\vec{PL}|</math>. | ||
{{Lösung versteckt|1= | |||
Wir bestimmen den Abstand zwischen der Geraden <math> g:\vec{x}= \begin{pmatrix} 2 \\ 3 \\ 2 \end{pmatrix}+r\cdot\begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix} </math> und dem Punkt <math>P(1|2|-3) </math>. | |||
1. Allgemeinen Verbindungsvektor <math>\vec{PL_r}</math> bestimmen: | |||
<math>L_r=(2+2r|3+r|2-r)</math> ist ein allgemeiner Punkt auf <math>g</math>, also ist <math>\vec{PL_r}=\begin{pmatrix} (2+2r)-1 \\ (3+r)-2 \\ (2-r)-(-3) \end{pmatrix}=\begin{pmatrix} 1+2r \\ 1+r \\ 5-r \end{pmatrix}</math> ein allgemeiner Verbindungsvektor. | |||
2. Den Parameter <math>r</math> so bestimmen, dass <math>\vec{PL_r}</math> orthogonal zum Richtungsvektor von <math>g</math> ist: | |||
Dafür muss gelten: <math>\begin{pmatrix} 1+2r \\ 1+r \\ 5-r \end{pmatrix}\ast \begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix}=0 </math> bzw. <math> 0=(1+2r)\cdot 2+(1+r)\cdot 1 + (5-r) \cdot (-1)=-2+6r</math>. Es folgt <math>r=\frac{1}{3}</math>. | |||
3. Abstand berechnen: | |||
Durch Einsetzen von <math>r</math> erhält man <math>\vec{PL}=\begin{pmatrix} \frac{5}{3} \\ \frac{4}{3} \\ \frac{14}{3} \end{pmatrix}</math> als kürzesten Verbindungsvektor. | |||
Also ist <math>d(P;g)=|\vec{PL}|=\sqrt{(\frac{5}{3})^2+(\frac{4}{3})^2+(\frac{14}{3})^2}=\frac{\sqrt{237}}{3}\approx 5,1316</math>. | |||
|2=Beispiel Verfahren Orthogonalität|3=Beispiel verbergen}} | |||
| 3=Merksatz}} | | 3=Merksatz}} | ||
| Zeile 414: | Zeile 447: | ||
<math> \Rightarrow L(-3|5|5) </math> | <math> \Rightarrow L(-3|5|5) </math> | ||
4. Abstand <math> | 4. Abstand zwischen <math>P</math> und <math>L</math> bestimmen: | ||
<math> | <math>|\vec{PL}|=\sqrt{(-3-(-2))^2+(5-3)^2+(5+10)^2}=\sqrt{30}\approx 5,477</math> | ||
Die Lichterkette muss mindestens <math>5,48</math> Meter lang sein. | Die Lichterkette muss mindestens <math>5,48</math> Meter lang sein. | ||
| Zeile 438: | Zeile 471: | ||
Du kannst mit der Maus den Punkt <math>D</math> verschieben. | Du kannst mit der Maus den Punkt <math>D</math> verschieben. | ||
<ggb_applet id="mftwqmc8" width= | <ggb_applet id="mftwqmc8" width="1000" height="470" /> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| Zeile 445: | Zeile 478: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Die Behauptung stimmt nicht. Den Flächeninhalt <math>A_\ | Die Behauptung stimmt nicht. Den Flächeninhalt <math>A_{\text{DBC}}</math> eines Dreiecks kann man bekanntermaßen mit der Formel <math>A_{\text{DBC}}=\frac{1}{2}\cdot g \cdot h</math> berechnen, wobei <math>g</math> die Länge der Grundseite ist. | ||
In dieser Aufgabe bleibt der Abstand <math>d(D;i)</math> immer gleich, da sich <math>D</math> auf einer zu <math>i</math> parallelen Geraden "bewegt". Also ist die Höhe <math>h</math> all dieser Dreiecke gleich. Deshalb ändert sich auch der Flächeninhalt <math>A_\ | In dieser Aufgabe bleibt der Abstand <math>d(D;i)</math> immer gleich, da sich <math>D</math> auf einer zu <math>i</math> parallelen Geraden "bewegt". Also ist die Höhe <math>h</math> all dieser Dreiecke gleich. Deshalb ändert sich auch der Flächeninhalt <math>A_{\text{DBC}}=\frac{1}{2}\cdot g \cdot h</math> nicht. | ||
|2=Lösung zu a) anzeigen|3=Lösung zu a) verbergen}} | |2=Lösung zu a) anzeigen|3=Lösung zu a) verbergen}} | ||
| Zeile 469: | Zeile 502: | ||
<math>\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}\ast \begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix}=0 </math> bzw. <math>(t-1)\cdot 1+(-7+3t)\cdot 3 + (1-4t) \cdot (-4)=0</math>. Es folgt <math>t=1</math>, also ist der Verbindungsvektor für <math>L(2|4|-2)</math> am kürzesten. Somit ist <math>h=d(B;j)=|\vec{BL}|=\sqrt{(2-2)^2+(4-8)^2+(-2-1)^2}=\sqrt{25}=5</math>. | <math>\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}\ast \begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix}=0 </math> bzw. <math>(t-1)\cdot 1+(-7+3t)\cdot 3 + (1-4t) \cdot (-4)=0</math>. Es folgt <math>t=1</math>, also ist der Verbindungsvektor für <math>L(2|4|-2)</math> am kürzesten. Somit ist <math>h=d(B;j)=|\vec{BL}|=\sqrt{(2-2)^2+(4-8)^2+(-2-1)^2}=\sqrt{25}=5</math>. | ||
Der Flächeninhalt des Dreiecks beträgt also <math>A_\ | Der Flächeninhalt des Dreiecks beträgt also <math>A_{\text{DBC}}=\frac{1}{2}\cdot g \cdot h=\frac{1}{2}\cdot \sqrt{58,5} \cdot 5\approx 19,12</math> Flächeneinheiten. | ||
|2=Lösung anzeigen|3=Lösung verbergen}} | |2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Zeile 481: | Zeile 514: | ||
Du kannst die Grafik mit deiner Maus drehen, um die Geraden aus anderen Perspektiven zu betrachten. | Du kannst die Grafik mit deiner Maus drehen, um die Geraden aus anderen Perspektiven zu betrachten. | ||
<ggb_applet id="mhdaxa3x" width=" | <ggb_applet id="mhdaxa3x" width="1000" height="470" /> | ||
{{Lösung versteckt|1= Damit <math>\overline{GH}</math> die kürzeste Verbindungsstrecke zwischen den windschiefen Geraden <math>g</math> und <math>h</math> ist, müssen beide Winkel <math>90^{\circ}</math> groß sein. | {{Lösung versteckt|1= Damit <math>\overline{GH}</math> die kürzeste Verbindungsstrecke zwischen den windschiefen Geraden <math>g</math> und <math>h</math> ist, müssen beide Winkel <math>90^{\circ}</math> groß sein. | ||
| Zeile 499: | Zeile 532: | ||
# Stelle den Verbindungsvektor <math>\vec{G_s H_t}</math> in Abhängigkeit von den Geradenparametern auf. | # Stelle den Verbindungsvektor <math>\vec{G_s H_t}</math> in Abhängigkeit von den Geradenparametern auf. | ||
# Bestimme nun die Parameter <math>s</math> und <math>t</math> so, dass der Verbindungsvektor <math>\vec{G_s H_t}</math> orthogonal zu den Richtungsvektoren von <math>g</math> und <math>h</math> ist. Du löst also das lineare Gleichungssystem mit den beiden Gleichungen <math>\vec{G_s H_t}\ast \vec{u} =0</math> und <math>\vec{G_s H_t}\ast \vec{v} =0</math>. | # Bestimme nun die Parameter <math>s</math> und <math>t</math> so, dass der Verbindungsvektor <math>\vec{G_s H_t}</math> orthogonal zu den Richtungsvektoren von <math>g</math> und <math>h</math> ist. Du löst also das lineare Gleichungssystem mit den beiden Gleichungen <math>\vec{G_s H_t}\ast \vec{u} =0</math> und <math>\vec{G_s H_t}\ast \vec{v} =0</math>. | ||
# Mit diesen Parametern erhältst du die Lotfußpunkte <math>G</math> und <math>H</math> und kannst den Abstand <math>d(g;h)=d( | # Mit diesen Parametern erhältst du die Lotfußpunkte <math>G</math> und <math>H</math> und kannst den Abstand <math>d(g;h)=|\vec{GH}|</math> bestimmen. | ||
{{Lösung versteckt|1= | |||
Wir bestimmen den Abstand der windschiefen Geraden <math> g:\vec{x}= \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix}+s\cdot\begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} </math> und <math> h:\vec{x}= \begin{pmatrix} 7 \\ 7 \\ 0 \end{pmatrix}+t\cdot\begin{pmatrix} 4 \\ -5 \\ 2 \end{pmatrix} </math>. | |||
# Geradenpunkte <math>G</math> und <math>H</math> in Abhängigkeit von dem jeweiligen Geradenparameter<br /><math>G_s(0|1+s|2+s)</math> und <math>H_t(7+4t|7-5t|2t)</math> | |||
# Verbindungsvektor <math>\vec{G_s H_t}</math> in Abhängigkeit von den Geradenparametern <math>t</math> und <math>s</math>:<br /> <math>\vec{G_sH_t}=\begin{pmatrix} 7+4t \\ 7-5t-(1+s) \\ 2t-(2+s) \end{pmatrix}=\begin{pmatrix} 7+4t \\ 6-5t-s \\ 2t-2-s \end{pmatrix}</math> | |||
# <math>s</math> und <math>t</math> so bestimmen, dass <math>\vec{G_s H_t}</math> orthogonal zu den Richtungsvektoren von <math>g</math> und <math>h</math> ist, also das lineare Gleichungssystem <math>\vec{G_s H_t}\ast \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} =0</math> und <math>\vec{G_s H_t}\ast\begin{pmatrix} 4 \\ -5 \\ 2 \end{pmatrix} =0</math> lösen:<br /> <math>0=(6-5t-s)\cdot 1+(2t-2-s) \cdot 1=4-3t-2s</math> und <math>0=(7+4t)\cdot 4+(6-5t-s)\cdot (-5)+(2t-2-s)\cdot 2=-6+45t+3t</math> liefert <math>s=2</math> und <math>t=0</math>. | |||
# Damit erhält man die Lotfußpunkte <math>G(0|3|4)</math> und <math>H(7|7|0)</math>. | |||
Also ist <math>d(g;h)=|\vec{GH}|=\sqrt{(7-0)^2+(7-3)^2+(4-0)^2}=\sqrt{81}=9</math>. | |||
|2=Beispiel zum Verfahren Gemeinsames Lot|3=Beispiel verbergen}} | |||
'''Verfahren Hilfsebene''' | '''Verfahren Hilfsebene''' | ||
Es gibt eine Ebene <math>E</math>, sodass <math>g</math> in <math>E</math> liegt und <math>h</math> parallel zu <math>E</math> ist. Für diese Ebene <math>E</math> ist dann der Abstand zwischen den Geraden <math>d(g,h)</math> gleich dem Abstand zwischen <math>E</math> und einem beliebigen Punkt <math>H</math> auf <math>h</math>. Jeder Normalenvektor von dieser Ebene <math>E</math> ist orthogonal zu den Richtungsvektoren von <math>g</math> und <math>h</math>. | Es gibt eine Ebene <math>E</math>, sodass <math>g</math> in <math>E</math> liegt und <math>h</math> parallel zu <math>E</math> ist. Für diese Ebene <math>E</math> ist dann der Abstand zwischen den Geraden <math>d(g,h)</math> gleich dem Abstand zwischen <math>E</math> und einem beliebigen Punkt <math>H</math> auf <math>h</math>. | ||
# Stelle die Ebenengleichung in Koordinatenform der Ebene <math>E</math> auf, sodass die Gerade <math>g</math> in <math>E</math> liegt und die Gerade <math>h</math> parallel zu <math>E</math> ist: Jeder Normalenvektor von dieser Ebene <math>E</math> ist orthogonal zu den Richtungsvektoren von den Geraden <math>g</math> und <math>h</math>. Bestimme also aus den Gleichungen <math>\vec{u}\ast\vec{n}=0</math> und <math>\vec{v}\ast\vec{n}=0</math> einen Normalenvektor <math>\vec{n}=\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix}</math>.<br /> Die Ebenengleichung in Koordinatenform ist dann <math>E:n_1\cdot x_1+ n_2\cdot x_2 +n_3\cdot x_3=b </math>.<br /> Die Gerade <math>g</math> soll in <math>E</math> liegen. Bestimme also <math>b</math>, indem du einen Punkt der Geraden <math>g</math> in die Ebenengleichung einsetzt. | |||
# Wähle einen beliebigen Punkt <math>H</math> auf der Geraden <math>h</math>. (Da <math>h</math> parallel zu <math>E</math> ist, haben alle Punkte von <math>h</math> den gleichen Abstand zu <math>E</math>.) | |||
# Bestimme mit der Formel für den Abstand eines Punktes von einer Ebene oder dem Lotfußpunktverfahren (siehe Abschnitt Abstand Punkt Ebene) den Abstand <math>d(E;H)</math>. So, wie wir die Ebene <math>E</math> konstruiert haben, ist nun der Abstand zwischen den windeschiefen Geraden <math>d(g;h)=d(E;H)</math>. | |||
{{Lösung versteckt|1= | |||
Wir bestimmen den Abstand der windschiefen Geraden <math> g:\vec{x}= \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix}+s\cdot\begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} </math> und <math> h:\vec{x}= \begin{pmatrix} 7 \\ 7 \\ 0 \end{pmatrix}+t\cdot\begin{pmatrix} 4 \\ -5 \\ 2 \end{pmatrix} </math>. | |||
Mit dem Verfahren Hilfsebene: | |||
# Ebenengleichung der Ebene <math>E</math>, sodass <math>g</math> in <math>E</math> liegt und <math>h</math> parallel zu <math>E</math> ist, aufstellen:<br /> Der Normalenvektor ist orthogonal zu den Richtungsvektoren von <math>g</math> und <math>h</math>, also gilt:<br /> <math>\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix}\ast \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} =0</math> und <math>\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix}\ast \begin{pmatrix} 4 \\ -5 \\ 2 \end{pmatrix} =0</math><br /> bzw. <math>0=n_2+n_3</math> und <math>0=4n_1-5n_2+2n_3</math>.<br /> Dieses Gleichungssystem ergibt <math>\vec{n}=\begin{pmatrix} -\frac{7}{4} \\ -1 \\ 1 \end{pmatrix}</math> als möglichen Normalenvektor.<br /> Also ist <math>E:-\frac{7}{4}\cdot x_1- x_2 + x_3=b </math>.<br /> Einen Punkt der Geraden <math>g</math> einsetzen, um <math>b</math> zu erhalten (denn die Gerade <math>g</math> soll in der Ebene <math>E</math> liegen):<br /> Wir nehmen den Punkt <math>(0|1|2)</math> auf <math>g</math>. Also ist <math>b=-\frac{7}{4}\cdot 0- 1 + 2=1</math> und insgesamt <math> E: -\frac{7}{4}\cdot x_1- x_2 + x_3=1</math>. | |||
# Einen beliebigen Punkt <math>H</math> auf der Geraden <math>h</math> wählen: Wir nehmen <math>H(7|7|0)</math>. | |||
# Abstand mit der Formel zur Berechnung des Abstandes zwischen einem Punkt und einer Ebene bestimmen:<br /> <math>d(g;h)=d(E;H)=\frac {|-\frac{7}{4}\cdot 7 + (-1)\cdot 7 + 1\cdot 0-1|}{\sqrt{(-\frac{7}{4}^2+(-1)^2+1^2}}=9</math> | |||
|2=Beispiel zum Verfahren Hilfsebene|3=Beispiel verbergen}} | |||
|3=Merksatz}} | |||
| Zeile 529: | Zeile 583: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Da die Tunnel einen Radius von <math>2,5</math>cm haben und die Geraden in dem Modell in der Mitte der jeweiligen Tunnel liegen, müssen die Geraden mindestens einen Abstand von <math>2,5+15+2,5=20</math> haben, damit die Tunnel nicht einstürzen. | Da die Tunnel jeweils einen Radius von <math>2,5</math>cm haben und die Geraden in dem Modell in der Mitte der jeweiligen Tunnel liegen, müssen die Geraden mindestens einen Abstand von <math>2,5+15+2,5=20</math>cm haben, damit die Tunnel nicht einstürzen. | ||
Wir bestimmen den Abstand zwischen den Geraden mithilfe einer Hilfsebene <math>E</math>, die parallel zur Geraden <math>h</math> ist und in der die Gerade <math>g</math> liegt. | Wir bestimmen den Abstand zwischen den Geraden mithilfe einer Hilfsebene <math>E</math>, die parallel zur Geraden <math>h</math> ist und in der die Gerade <math>g</math> liegt. | ||
| Zeile 535: | Zeile 589: | ||
<math>\begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix}\ast \vec{n}=0</math> | <math>\begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix}\ast \vec{n}=0</math> | ||
und <math>\begin{pmatrix} 3 \\ -4 \\ 1 \end{pmatrix}\ast \vec{n}=0</math>. Es folgt <math>n_1=\frac{2}{3} n_3</math> und <math>n_2=\frac{3}{4} n_3</math>. Also ist <math>\vec{n}=\begin{pmatrix} \frac{2}{3} \\ \frac{3}{4} \\ 1 \end{pmatrix}</math> ein Normalenvektor von <math>E</math>. | und <math>\begin{pmatrix} 3 \\ -4 \\ 1 \end{pmatrix}\ast \vec{n}=0</math>. Es folgt <math>n_1=\frac{2}{3} n_3</math> und <math>n_2=\frac{3}{4} n_3</math>. Also ist <math>\vec{n}=\begin{pmatrix} \frac{2}{3} \\ \frac{3}{4} \\ 1 \end{pmatrix}</math> ein Normalenvektor von <math>E</math>. | ||
Somit ist <math>E:\frac{2}{3}\cdot x_1+ \frac{3}{4}\cdot x_2 + x_3=b</math>. Einsetzen vom Punkt <math>(1|1|1)</math> auf der Geraden <math>g</math> in diese Gleichung ergibt <math>b=\frac{2}{3}\cdot 1+ \frac{3}{4}\cdot 1 + 1 = \frac{29}{12}</math>. | |||
Die Koordinatenform von <math>E</math> lautet also <math>E:\frac{2}{3}\cdot x_1+ \frac{3}{4}\cdot x_2 + x_3=\frac{29}{12}</math>. | |||
Nehme den Punkt <math>H(6|6|18)</math> auf der Geraden <math>h</math>. | Nehme den Punkt <math>H(6|6|18)</math> auf der Geraden <math>h</math>. | ||
Da der Abstand zwischen den Geraden gleich dem Abstand zwischen der Ebene <math>E</math> und einem beliebigen Punkt auf der zu <math>E</math> parallelen Geraden <math>h</math> ist, erhält man nun mit der Formel für den Abstand eines Punktes von einer Ebene <math>d(g;h)=d(E;H)=\frac{|\frac{2}{3}\cdot 6+\frac{3}{4}\cdot 6+18- | Da der Abstand zwischen den Geraden gleich dem Abstand zwischen der Ebene <math>E</math> und einem beliebigen Punkt auf der zu <math>E</math> parallelen Geraden <math>h</math> ist, erhält man nun mit der Formel für den Abstand eines Punktes von einer Ebene <math>d(g;h)=d(E;H)=\frac {|\frac{2}{3}\cdot 6+ \frac{3}{4}\cdot 6 + 1\cdot 18-\frac{29}{12}|}{\sqrt{(\frac{2}{3}^2+(\frac{3}{4})^2+1^2}}=17</math>. | ||
Die Geraden haben also einen kleineren Abstand als <math>20</math> | Die Geraden haben also einen kleineren Abstand als <math>20</math>cm. Das heißt, die Tunnel sind nicht überall mindestens <math>15</math>cm voneinander entfernt (sondern an einer Stelle nur <math>17</math>cm-<math>2\cdot 2,5</math>cm<math>=12</math>cm) und sie werden einstürzen. | ||
Die einzige Lösung für die Maulwürfe ist es, an der kritischen Stelle eine gemeinsame Höhle zu bauen. :) | Die einzige Lösung für die Maulwürfe ist es, an der kritischen Stelle eine gemeinsame Höhle zu bauen. :) | ||
| Zeile 547: | Zeile 603: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Die Geraden haben einen Abstand von <math> | Die Geraden haben einen Abstand von <math>17</math>cm. Zwischen den Tunneln sind also an einer Stelle nur <math>12</math>cm Erde und sie werden einstürzen. | ||
Dann bauen die beiden Maulwürfe an der kritischen Stelle einfach eine gemeinsame Höhle. :) | Dann bauen die beiden Maulwürfe an der kritischen Stelle einfach eine gemeinsame Höhle. :) | ||
| Zeile 554: | Zeile 610: | ||
| 3=Arbeitsmethode}} | | 3=Arbeitsmethode}} | ||
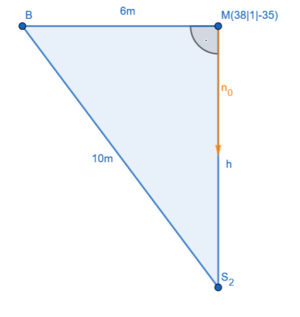
{{Box | 1=Aufgabe | {{Box | Aufgabe 14: U-Boote | | ||
Die Routen zweier U-Boote können durch die Geraden <math>g:\vec{x}=\begin{pmatrix} 140 \\ -70 \\ -1120 \end{pmatrix}+s\cdot \begin{pmatrix} 23 \\ 0 \\ 47 \end{pmatrix}</math> und <math>h:\vec{x}=\begin{pmatrix} -1130 \\ -270 \\ 450 \end{pmatrix}+t\cdot \begin{pmatrix} 17 \\ 0 \\ 37 \end{pmatrix}</math> beschrieben werden. Dabei entspricht eine Längeneinheit einem Meter. Das Radar der U-Boote hat eine Reichweite von <math>500</math> Metern. | |||
Können die U-Boote das jeweils andere U-Boot auf dem Radar erkennen? | |||
{{Lösung versteckt|1= | |||
Die Geraden haben einen Abstand von <math>200</math>LE, das heißt, die Routen der U-Boote sind einer Stelle nur <math>200</math> Meter voneinander entfernt. Es könnte also passieren, dass die U-Boote sich gegenseitig auf dem Radar erkennen können. Allerdings weiß man natürlich nicht, wann sich die U-Boote an welcher Stelle der Route befinden. Je nachdem, wann und wo sie starten und mit welcher Geschwindigkeit sie fahren, könnte es auch sein, dass sie die ganze Zeit mehr als <math>500</math> Meter voneinander entfernt sind. | |||
Der Lösungsweg zur Abstandsbestimmung der Geraden, hier mit dem Verfahren Gemeinsames Lot: | |||
Die Geradenpunkte <math>G</math> und <math>H</math> in Abhängigkeit von dem jeweiligen Geradenparameter sind | |||
<math>G_s(140+23s|-70|-1120+47s)</math> und <math>H_t(-1130+17t|-270|450+37t)</math>. | |||
Der Verbindungsvektor <math>\vec{G_s H_t}</math> in Abhängigkeit von den Geradenparametern <math>t</math> und <math>s</math> ist dann gegeben durch | |||
<math>\vec{g_sH_t}=\begin{pmatrix} -1270+17t-23s \\ -200 \\ 1570+37t-47s \end{pmatrix}</math> | |||
Wenn der Verbindungsvektor <math>\vec{G_s H_t}</math> orthogonal zu den Richtungsvektoren von <math>g</math> und <math>h</math> ist, ist er am kürzesten. Es muss also <math>\vec{G_s H_t}\ast \begin{pmatrix} 23 \\ 0 \\ 47 \end{pmatrix} =0</math> und <math>\vec{G_s H_t}\ast \begin{pmatrix} 17 \\ 0 \\ 37 \end{pmatrix} =0</math> gelten. Daraus ergibt sich das lineare Gleichungssystem <math>44580+2130t-2738s=0</math> und <math>36500+1658t-2130s</math>. | |||
Es folgt <math>t=-\frac{23950}{13}</math> und <math>s=-\frac{18420}{13}</math>. | |||
Damit erhält man die Lotfußpunkte <math>G(-\frac{421840}{13}|-70|-\frac{880300}{13})</math> und <math>H(-\frac{421840}{13}|-270|-\frac{880300}{13})</math>. | |||
Also ist <math>d(g;h)=|\vec{GH}|=\sqrt{(-\frac{421840}{13}-(-\frac{421840}{13}))^2+(-70-(-270))^2+(-\frac{880300}{13}-(-\frac{880300}{13}))^2}=\sqrt{0^2+200^2+0^2}=200</math>. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| Arbeitsmethode| Farbe={{Farbe|orange}} }} | |||
{{Box | 1=Aufgabe 15: Windschiefe Geraden, Lotfußpunkte, Abstände zuordnen | 2= | |||
Bei dieser Aufgabe gibt es drei Geradenpaare <math>g</math> und <math>h</math>, die jeweils windschief zueinander liegen. Schiebe zuerst die Geradenpaare auf das Feld mit der entsprechenden Nummer. | Bei dieser Aufgabe gibt es drei Geradenpaare <math>g</math> und <math>h</math>, die jeweils windschief zueinander liegen. Schiebe zuerst die Geradenpaare auf das Feld mit der entsprechenden Nummer. | ||
Ordne ihnen dann die jeweiligen Lotfußpunkte <math>G</math> und <math>H</math> sowie den entsprechenden Abstand zwischen den Geraden zu. | Ordne ihnen dann die jeweiligen Lotfußpunkte <math>G</math> und <math>H</math> sowie den entsprechenden Abstand zwischen den Geraden zu. | ||
| Zeile 577: | Zeile 659: | ||
Also kann man den Abstand der Geraden direkt an der <math>x_3</math>-Koordinate des Stützvektors der Geraden <math>h</math> ablesen: <math>d(g;h)=|1|=1</math>. | Also kann man den Abstand der Geraden direkt an der <math>x_3</math>-Koordinate des Stützvektors der Geraden <math>h</math> ablesen: <math>d(g;h)=|1|=1</math>. | ||
Außerdem liegt <math>G(0|0|0)</math> auf <math>g</math> und <math>H(0|0|1)</math> auf <math>h</math> und der Verbindungsvektor <math>\vec{GH}=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}</math> ist orthogonal zu den Richtungsvektoren <math>\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}</math> und <math>\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}</math> beider Geraden. Also sind diese beiden Punkte die Lotfußpunkte | Außerdem liegt <math>G(0|0|0)</math> auf <math>g</math> und <math>H(0|0|1)</math> auf <math>h</math> und der Verbindungsvektor <math>\vec{GH}=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}</math> ist orthogonal zu den Richtungsvektoren <math>\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}</math> und <math>\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}</math> beider Geraden. Also sind diese beiden Punkte die Lotfußpunkte, weshalb das gemeinsame Lot insbesondere auf der <math>x_3</math>-Achse liegt. | ||
(Letzteres kann man auch daran erkennen, dass <math>g</math> entlang der <math>x_1</math>-Achse verläuft und <math>h</math> parallel zur <math>x_2</math>-Achse und nicht in <math>x_1</math>-Richtung verschoben ist (der Stützvektor von <math>h</math> hat die <math>x_1</math>-Koordinate <math>0</math>). Beide Geraden schneiden also die <math>x_3</math>-Achse und sind parallel zur <math>x_1</math><math>x_2</math>-Ebene bzw. liegen in dieser Ebene.) | |||
| Zeile 583: | Zeile 667: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Da der Richtungsvektor von <math>h</math> im Eintrag der <math>x_2</math>-Koordinate <math>0</math> ist, ist <math>h</math> parallel zur <math>x_1</math> | Da der Richtungsvektor von <math>h</math> im Eintrag der <math>x_2</math>-Koordinate <math>0</math> ist, ist <math>h</math> parallel zur <math>x_1</math><math>x_3</math>-Ebene. <math>g</math> liegt in der <math>x_1</math><math>x_3</math>-Ebene. (Da die Richtungsvektoren von <math>g</math> und <math>h</math> keine Vielfachen voneinander sind, sind die Geraden nicht parallel zueinander, was aber ja auch schon in der Aufgabenstellung gesagt wurde.) Also kann man den Abstand der Geraden direkt am Unterschied der <math>x_2</math>-Koordinaten der Stützvektoren der beiden Geraden ablesen: <math>d(g;h)=|2-0|=2</math>. Da man aber nicht genau weiß, wo <math>g</math> liegt (man kennt nur den Richtungsvektor), kann man auch nicht sagen, wo genau die Lotfußpunkte liegen. | ||
|2=Möglichen Lösungsweg für 3. anzeigen|3=Lösungsweg verbergen}} | |2=Möglichen Lösungsweg für 3. anzeigen|3=Lösungsweg verbergen}} | ||
| | | Farbe={{Farbe|grün|dunkel}} }} | ||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Unterwegs_in_3-D_–_Punkte,_Vektoren,_Geraden_und_Ebenen_im_Raum#Kapitelauswahl}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 23. Juni 2021, 18:11 Uhr
Einstieg
Im Folgenden werden nun die Verfahren für die verschiedenen Abstandsprobleme wiederholt. Je nachdem, was du noch üben willst, kannst du dir den jeweiligen Abschnitt dieses Lernpfadkapitels anschauen.
Abstand eines Punktes von einer Ebene
Die folgenden Aufgaben kannst du entweder mit dem Lotfußpunktverfahren oder der Formel für den Abstand eines Punktes von einer Ebene lösen.
Abstand eines Punktes von einer Geraden
Abstand zweier windschiefer Geraden