Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
(GeoGebra-Größe angepasst) Markierung: Quelltext-Bearbeitung 2017 |
||
| (38 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 25: | Zeile 25: | ||
}} | }} | ||
Wie du nun eine Parametergleichung durch zwei gegebene Punkte aufstellst, wird im folgenden Video erklärt: | Wie du nun eine Parametergleichung durch zwei gegebene Punkte aufstellst, wird im folgenden Video erklärt: | ||
{{#ev:youtube|cCetvDxbTQk}} | |||
{{ | {{Box | ||
|Aufgabe 1: Parameter einer Geradengleichung | |||
|Im Folgenden kannst du sehen, wie die Gerade vom Stützpunkt <math>A</math>, Richtungsvektor <math>\vec{v}</math> und Parameter <math>t</math> abhängt. Wähle verschiedene Stützpunkte und Richtungsvektoren und verändere den Parameter. Wo liegt der Punkt <math>P</math>, wenn du <math>t < 0</math>, <math>t = 0</math> und <math>t > 0</math> wählst? Was bedeutet dies anschaulich? Dazu kannst du dir auch die Gerade <math>g</math> anzeigen lassen. | |||
<ggb_applet id="avyg7hmy" width="1000" height="509" /> | |||
< | {{Lösung versteckt | ||
|* Für <math>t < 0</math> liegt der Punkt <math>P</math> hinter dem Punkt <math>A</math>, d.h. man geht auf der Gerade vom Stützpunkt aus gesehen rückwärts. | |||
* Für <math>t = 0</math> liegt der Punkt <math>P</math> genau auf dem Punkt <math>A</math>, d.h. sie sind identisch, man befindet sich also genau auf dem Stützpunkt. | |||
< | * Für <math>t > 0</math> liegt der Punkt <math>P</math> vor dem Punkt <math>A</math>, d.h. man geht auf der Gerade vom Stützpunkt aus gesehen vorwärts. | ||
|Lösung anzeigen | |||
|Lösung verbergen | |||
}} | |||
|Arbeitsmethode | |||
|Farbe={{Farbe|orange}} | |||
}} | |||
{{Box | {{Box | ||
|Aufgabe | |Aufgabe 2: Geradengleichung aufstellen (zwei gegebene Punkte) | ||
|Bearbeite entweder die analoge Aufgabe (I) oder die digitale Aufgabe (II): | |Bearbeite nun entweder die analoge Aufgabe (I) oder die digitale Aufgabe (II): | ||
(I) Die Gerade <math>g</math> geht durch die Punkte <math>A</math> und <math>B</math>. Gib zwei Gleichungen für <math>g</math> an. | (I) Die Gerade <math>g</math> geht durch die Punkte <math>A</math> und <math>B</math>. Gib zwei Gleichungen für <math>g</math> an. | ||
| Zeile 49: | Zeile 58: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Zwei mögliche Geraden sind <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ | |Wie du im obigen Video gesehen hast, gibt es unendlich viele Lösungen, denn es sind immer Vielfache des Richtungsvektors möglich. Daher ist es möglich, dass deine Lösung hier zwar nicht aufgefürt, aber dennoch korrekt ist. Dazu überprüfe, ob dein Richtungsvektor ein Vielfaches einer der angegeben Richtungsvektoren ist. Beachte das auch bei allen folgenden Aufgaben! | ||
Zwei mögliche Geraden sind <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} + s \cdot \begin{pmatrix} 4 \\ -6 \\ 5 \end{pmatrix}, s \in \mathbb{R} </math> und <math>g \colon \vec{x} = \begin{pmatrix} 5 \\ -4 \\ 7 \end{pmatrix} + t \cdot \begin{pmatrix} -4 \\ 6 \\ -5 \end{pmatrix}, t \in \mathbb{R} </math>. | |||
|Lösung Aufgabe a) anzeigen | |Lösung Aufgabe a) anzeigen | ||
|Lösung Aufgabe a) verbergen | |Lösung Aufgabe a) verbergen | ||
| Zeile 55: | Zeile 66: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Zwei mögliche Geraden sind <math>g \colon \vec{x} = \begin{pmatrix} -3 \\ - | |Zwei mögliche Geraden sind <math>g \colon \vec{x} = \begin{pmatrix} -3 \\ -2 \\ 9 \end{pmatrix} + s \cdot \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix}, s \in \mathbb{R} </math> und <math>g \colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} -3 \\ -2 \\ 6 \end{pmatrix}, t \in \mathbb{R} </math>. | ||
|Lösung Aufgabe b) anzeigen | |Lösung Aufgabe b) anzeigen | ||
|Lösung Aufgabe b) verbergen | |Lösung Aufgabe b) verbergen | ||
| Zeile 61: | Zeile 72: | ||
(II) Ordne jeweils die zwei Punkte A und B der Parametergleichung der Geraden durch A und B zu. | (II) Ordne jeweils die zwei Punkte A und B der Parametergleichung der Geraden durch A und B zu. | ||
{{LearningApp|width=100%|height=500px|app= | {{LearningApp|width=100%|height=500px|app=20364580}} | ||
|Arbeitsmethode | |Arbeitsmethode | ||
|Farbe={{Farbe|orange}} | |Farbe={{Farbe|orange}} | ||
| Zeile 69: | Zeile 80: | ||
{{Box | {{Box | ||
|Aufgabe | |Aufgabe 3: Geradengleichung aufstellen aus Punkt und Richtungsvektor | ||
|Stelle jeweils eine Geradengleichung auf. | |Stelle jeweils eine Geradengleichung auf. | ||
'''a)''' Die Gerade <math>g</math> geht durch den Punkt <math>P( | '''a)''' Die Gerade <math>g</math> geht durch den Punkt <math>P(1|{-}1|2)</math> und hat den Richtungsvektor <math>\vec{v} = \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix}</math>. | ||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |Überlege dir wie der Stützvektor der Geraden lauten muss und stelle dann die passende Geradengleichung mit dem Richtungsvektor auf. | ||
|Tipp Aufgabe a) anzeigen | |Tipp Aufgabe a) anzeigen | ||
|Tipp Aufgabe a) verbergen | |Tipp Aufgabe a) verbergen | ||
}} | }} | ||
'''b)''' | '''b)''' Stelle eine Geradengleichung für die <math>x_1</math>-Achse auf. | ||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |Überlege dir einen geschickten Aufpunkt; wie muss dann der Richtungsvektor aussehen? | ||
|Tipp Aufgabe b) anzeigen | |Tipp Aufgabe b) anzeigen | ||
|Tipp Aufgabe b) verbergen | |Tipp Aufgabe b) verbergen | ||
}} | }} | ||
'''c)''' Die Gerade <math>g</math> geht durch den | '''c)''' Die Gerade <math>g</math> geht durch den Punkt <math>P(2|{-}2|4)</math> und verläuft parallel zur Geraden <math>h: \vec{x} = \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}, r \in \mathbb{R} </math>. | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Diese Aufgabe funktioniert ähnlich zu | |Wann verlaufen zwei Vektoren parallel zueinander? Übertrage diese Kenntniss auf Geraden. | ||
|Tipp Aufgabe | |Tipp Aufgabe c) anzeigen | ||
|Tipp Aufgabe | |Tipp Aufgabe c) verbergen | ||
}} | |||
'''d)''' Die Gerade <math>g</math> geht durch den Punkt <math>P(1|{-}1|{-}2)</math> und verläuft parallel zur <math>x_1</math>-Achse. | |||
'''e)''' Die Gerade <math>g</math> geht durch den einen beliebigen Punkt <math>P(p_1|p_2|p_3)</math> und verläuft parallel zur <math>x_3</math>-Achse. | |||
{{Lösung versteckt | |||
|Diese Aufgabe funktioniert ähnlich zu d). | |||
|Tipp Aufgabe e) anzeigen | |||
|Tipp Aufgabe e) verbergen | |||
}} | }} | ||
| Zeile 99: | Zeile 120: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} | |Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix} + s \cdot \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix}, s \in \mathbb{R} </math>. | ||
|Lösung Aufgabe a) anzeigen | |Lösung Aufgabe a) anzeigen | ||
|Lösung Aufgabe a) verbergen | |Lösung Aufgabe a) verbergen | ||
| Zeile 105: | Zeile 126: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Eine mögliche Gerade ist <math> | |Eine mögliche Gerade ist <math>x_1 \colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, s \in \mathbb{R} </math> oder noch einfacher <math>x_1 \colon \vec{x} = s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, s \in \mathbb{R} </math> | ||
|Lösung Aufgabe b) anzeigen | |Lösung Aufgabe b) anzeigen | ||
|Lösung Aufgabe b) verbergen | |Lösung Aufgabe b) verbergen | ||
| Zeile 111: | Zeile 132: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} | |Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix} + s \cdot \begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}, s \in \mathbb{R} </math>. | ||
|Lösung Aufgabe c) anzeigen | |Lösung Aufgabe c) anzeigen | ||
|Lösung Aufgabe c) verbergen | |Lösung Aufgabe c) verbergen | ||
}} | |||
{{Lösung versteckt | |||
|Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ -1 \\ -2 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, s \in \mathbb{R} </math>. | |||
|Lösung Aufgabe d) anzeigen | |||
|Lösung Aufgabe d) verbergen | |||
}} | |||
{{Lösung versteckt | |||
|Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}, s \in \mathbb{R} </math>. | |||
|Lösung Aufgabe e) anzeigen | |||
|Lösung Aufgabe e) verbergen | |||
}} | }} | ||
| Zeile 121: | Zeile 154: | ||
===Punktprobe=== | ===Punktprobe=== | ||
Wie du überprüfst, ob ein gegebener Punkt auf einer gegebenen Gerade | Wie du überprüfst, ob ein gegebener Punkt auf einer gegebenen Gerade oder daneben liegt, kannst du [https://www.youtube.com/watch?v=1kJ9Nq8zXlI hier] noch einmal nachschauen. | ||
{{Box | {{Box | ||
| Zeile 132: | Zeile 163: | ||
{{Box | {{Box | ||
|Aufgabe | |Aufgabe 4: Punktprobe mit einer Geraden I | ||
|Überprüfe, ob der Punkt <math>P</math> auf der Geraden <math>g</math> liegt. | |Überprüfe, ob der Punkt <math>P</math> auf der Geraden <math>g</math> liegt. | ||
| Zeile 140: | Zeile 171: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Die Punktprobe ist erfüllt | |Die Punktprobe ist erfüllt, denn: | ||
<math>\begin{pmatrix} 2 \\ 3 \\ -1 \end{pmatrix} = \begin{pmatrix} 7 \\ 0 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 5 \\ -3 \\ 5 \end{pmatrix} | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
2 &&\; = \;&& 7 &&\; + \;&& 5r \\ | |||
3 &&\; = \;&& 0 &&\; - \;&& 3r \\ | |||
-1 &&\; = \;&& 4 &&\; + \;&& 5r | |||
\end{alignat}\right\vert | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
r &&\; = \;&& -1 \\ | |||
r &&\; = \;&& -1 \\ | |||
r &&\; = \;&& -1 | |||
\end{alignat}\right\vert</math> | |||
Somit liegt der Punkt <math>P</math> auf der Geraden <math>g</math>. | |||
|Lösung Aufgabe a) anzeigen | |Lösung Aufgabe a) anzeigen | ||
|Lösung Aufgabe a) verbergen | |Lösung Aufgabe a) verbergen | ||
| Zeile 146: | Zeile 193: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Die Punktprobe ist nicht erfüllt, | |Die Punktprobe ist nicht erfüllt, denn: | ||
<math>\begin{pmatrix} 2 \\ -1 \\ -1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 3 \\ 3 \end{pmatrix} | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
2 &&\; = \;&& 1 &&\; + \;&& r \\ | |||
-1 &&\; = \;&& 0 &&\; + \;&& 3r \\ | |||
-1 &&\; = \;&& 1 &&\; + \;&& 3r | |||
\end{alignat}\right\vert | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
r &&\; = \;&& 1 \\ | |||
r &&\; = \;&& -\frac{1}{3} \\ | |||
r &&\; = \;&& -\frac{2}{3} | |||
\end{alignat}\right\vert</math> | |||
Es ergibt sich ein Widerspruch. Somit liegt der Punkt <math>P</math> nicht auf der Geraden <math>g</math>. | |||
|Lösung Aufgabe b) anzeigen | |Lösung Aufgabe b) anzeigen | ||
|Lösung Aufgabe b) verbergen | |Lösung Aufgabe b) verbergen | ||
| Zeile 156: | Zeile 219: | ||
{{Box | {{Box | ||
|Aufgabe | |Aufgabe 5: Punktprobe mit einer Geraden II | ||
|Für | |Für welche Werte <math> s, r \in \mathbb{R} </math> liegt der Punkt <math>P</math> auf der Geraden <math>g: \vec{x} = \begin{pmatrix} 9 \\ -s \\ 2s \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} </math>? | ||
'''a)''' <math>P(13|3|0)</math> | '''a)''' <math>P(13|3|0)</math> | ||
'''b)''' <math>P( | '''b)''' <math>P(5|{-}2|0)</math> | ||
{{Lösung versteckt | |||
|Berechne zunächst mithilfe der ersten Gleichung einen Wert für <math>r</math>. Was könnte man nun machen? | |||
|Tipp 1 Aufgabe a) und b) anzeigen | |||
|Tipp 1 Aufgabe a) und b) verbergen | |||
}} | |||
{{Lösung versteckt | |||
|Setze nun den ausgerechneten Wert für <math>r</math> in die beiden anderen Gleichungen ein und berechne <math>s</math>. | |||
|Tipp 2 Aufgabe a) und b) anzeigen | |||
|Tipp 2 Aufgabe a) und b) verbergen | |||
}} | |||
{{Lösung versteckt | {{Lösung versteckt | ||
|Die Punktprobe ist | |Die Punktprobe ist erfüllt, denn: | ||
<math>\begin{pmatrix} 13 \\ 3 \\ 0 \end{pmatrix} = \begin{pmatrix} 9 \\ -s \\ 2s \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
13 &&\; = \;&& 9 &&\; + \;&& 2r \\ | |||
3 &&\; = \;&& -s &&\; + \;&& r \\ | |||
0 &&\; = \;&& 2s &&\; + \;&& r | |||
\end{alignat}\right\vert | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
r &&\; = \;&& 2 \\ | |||
3 &&\; = \;&& -s &&\; + \;&& 2 \\ | |||
0 &&\; = \;&& 2s &&\; + \;&& 2 | |||
\end{alignat}\right\vert | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
r &&\; = \;&& 2 \\ | |||
s &&\; = \;&& -1 \\ | |||
s &&\; = \;&& -1 | |||
\end{alignat}\right\vert</math> | |||
Somit liegt der Punkt <math>P</math> für <math>r = 2</math> und <math>s = -1</math> auf der Geraden <math>g</math>. | |||
|Lösung Aufgabe a) anzeigen | |Lösung Aufgabe a) anzeigen | ||
|Lösung Aufgabe a) verbergen | |Lösung Aufgabe a) verbergen | ||
| Zeile 170: | Zeile 267: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |Es gibt keine Lösung, denn: | ||
<math>\begin{pmatrix} 5 \\ -2 \\ 0 \end{pmatrix} = \begin{pmatrix} 9 \\ -s \\ 2s \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
5 &&\; = \;&& 9 &&\; + \;&& 2r \\ | |||
-2 &&\; = \;&& -s &&\; + \;&& r \\ | |||
0 &&\; = \;&& 2s &&\; + \;&& r | |||
\end{alignat}\right\vert | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
r &&\; = \;&& -2 \\ | |||
-2 &&\; = \;&& -s &&\; + \;&& -2 \\ | |||
0 &&\; = \;&& 2s &&\; + \;&& -2 | |||
\end{alignat}\right\vert | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
r &&\; = \;&& 2 \\ | |||
s &&\; = \;&& 0 \\ | |||
s &&\; = \;&& 1 | |||
\end{alignat}\right\vert</math> | |||
Es ergibt sich ein Widerspruch, weshalb keine Werte für Punkt <math>s, r</math> gibt, sodass der Punkt <math>P</math> auf der Geraden <math>g</math> liegt. | |||
|Lösung Aufgabe b) anzeigen | |Lösung Aufgabe b) anzeigen | ||
|Lösung Aufgabe b) verbergen | |Lösung Aufgabe b) verbergen | ||
| Zeile 177: | Zeile 296: | ||
|Arbeitsmethode | |Arbeitsmethode | ||
}} | }} | ||
Hier noch eine Aufgabe zu Geraden mit besonderen Lagen im Koordinatensystem: | |||
{{Box | |||
|Aufgabe 6: Besondere Geraden im Raum | |||
|Kreuze alle(!) richtigen Antworten an! | |||
{{LearningApp|width=100%|height=500px|app=p221zv0i321}} | |||
|Arbeitsmethode | |||
|Farbe={{Farbe|grün|dunkel}} | |||
}} | |||
===Spurpunkte einer Geraden=== | ===Spurpunkte einer Geraden=== | ||
Wie du die Spurpunkte, also die Schnittpunkte der Geraden mit den Koordinatenebenen bestimmst, | Wie du die Spurpunkte, also die Schnittpunkte der Geraden mit den Koordinatenebenen bestimmst, kannst du hier noch einmal nachvollziehen: | ||
{{#ev:youtube|OCO28fT5Aww}} | |||
Falls du nicht mehr weißt, was die Koordinatenebenen sind, kannst unter folgendem Tipp noch einmal dein Wissen auffrischen: | Falls du nicht mehr weißt, was die Koordinatenebenen sind, kannst unter folgendem Tipp noch einmal dein Wissen auffrischen: | ||
| Zeile 191: | Zeile 323: | ||
}} | }} | ||
{{Box | {{Box | ||
| | |Aufgabe 7: Spurpunkte einer Geraden (Besondere Lage) | ||
|Hier kannst du dir die Spurpunkte von verschiedenen Geraden anzeigen lassen. Dazu kannst du den Aufpunktvektor <math>\vec{a}</math> und den Richtungsvektor <math>\vec{u}</math> mit den Schiebereglern entsprechend anpassen. Anschließend kannst du dir die drei Spurpunkte und ggf. auch die Ebenen anzeigen lassen, indem du das entsprechende Feld ankreuzt. Dann kannst du dir die Koordinatebenen mit den verschiedenen Schnittpunkten anzeigen lassen: | |||
| | <ggb_applet id="ynkzgreu" width="1000" height="571" /> | ||
Untersuche die Geraden, die aus folgenden Aufpunkt- und Richtungsvektoren hervorgehen, auf Spurpunkte und schreibe die Spurpunkte auf. Was sagt die Lage der Geraden über die Anzahl der Spurpunkte aus? | |||
'''a)''' <math>\vec{a} = \begin{pmatrix} 3 \\ 1 \\ -1 \end{pmatrix}, \vec{u} = \begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix}</math> | |||
'''b)''' <math>\vec{a} = \begin{pmatrix} 1,5 \\ 3 \\ -2 \end{pmatrix}, \vec{u} = \begin{pmatrix} 3 \\ 0 \\ 2 \end{pmatrix}</math> | |||
'''c)''' <math>\vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \vec{u} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix}</math> | |||
'''d)''' <math>\vec{a} = \begin{pmatrix} 5 \\ 0 \\ 1 \end{pmatrix}, \vec{u} = \begin{pmatrix} 3 \\ 0 \\ 1,5 \end{pmatrix}</math> | |||
{{Lösung versteckt | |||
|Betrachte mal ggf. vorhandene Parallelitäten der Geraden zu den Koordinatenebenen. Fällt dir nun etwas auf? | |||
|Tipp für alle Aufgaben anzeigen | |||
|Tipp für alle Aufgaben verbergen | |||
}} | }} | ||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |Die drei Spurpunkte lauten <math>S_{12}(4,5|0,5|0)</math>, <math>S_{13}(6|0|1)</math> und <math>S_{23}(0|2|{-}3)</math>. Da die Gerade nicht parallel zu den Koordinatenebenen verläuft, besitzt sie drei Spurpunkte. | ||
| | |Lösung Aufgabe a) anzeigen | ||
| | |Lösung Aufgabe a) verbergen | ||
}} | |||
{{Lösung versteckt | |||
|Die zwei Spurpunkte lauten <math>S_{12}(4,5|3|0)</math> und <math>S_{23}(0|3|{-}3)</math>. Da die Gerade parallel zur <math>x_1x_3</math>-Ebene verläuft, hat sie keinen Schnittpunkt mit dieser und besitzt folglich nur zwei Spurpunkte. | |||
|Lösung Aufgabe b) anzeigen | |||
|Lösung Aufgabe b) verbergen | |||
}} | }} | ||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |Der einzige Spurpunkt lautet <math>S_{23}(0|2|3)</math>. Da die Gerade sowohl parallel zur <math>x_1x_2</math>-Ebene als auch parallel zur <math>x_1x_3</math>-Ebene verläuft, hat sie keine Schnittpunkte mit diesen und besitzt folglich nur einen Spurpunkt. | ||
| | |Lösung Aufgabe c) anzeigen | ||
| | |Lösung Aufgabe c) verbergen | ||
}} | }} | ||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |Die zwei Spurpunkte lauten <math>S_{12}(3|0|0)</math> und <math>S_{23}(0|0|{-}1,5)</math>. Da die Gerade innerhalb der <math>x_1x_3</math>-Ebene verläuft, hat sie unendlich viele Schnittpunkte mit dieser. | ||
| | |Lösung Aufgabe d) anzeigen | ||
| | |Lösung Aufgabe d) verbergen | ||
}} | }} | ||
| | |Arbeitsmethode | ||
|Farbe={{Farbe|orange}} | |||
}} | }} | ||
{{Box | |||
|Aufgabe 8: Spurpunkte einer Geraden | |||
|Berechne die Spurpunkte der Geraden <math>g</math>. | |||
< | '''a)''' <math>g \colon \vec{x} = \begin{pmatrix} 7 \\ 0 \\ 7 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}, r \in \mathbb{R} </math> | ||
'''b)''' <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix}, r \in \mathbb{R} </math> | |||
'''c)''' <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 0 \\ -4 \end{pmatrix}, r \in \mathbb{R} </math> | |||
{{Lösung versteckt | {{Lösung versteckt | ||
|Schnittpunkt <math>S_{13}</math> der Geraden <math>g</math> mit der <math>x_1x_3</math>-Ebene: <math>\vec{S_{13}} = \begin{pmatrix} | |# Für den Schnittpunkt <math>S_{12}</math> der Geraden <math>g</math> mit der <math>x_1x_2</math>-Ebene setze die <math>x_3</math>-Koordinate <math>= 0</math> und forme nach <math>r</math> um: <math>0 = 7 + r \cdot 1 \Leftrightarrow r = -7</math>. Setze nun <math>r = -7</math> in der Geradengleichung ein, um den Schnittpunkt <math>S_{12}</math> zu erhalten: <math>\vec{S_{12}} = \begin{pmatrix} 7 \\ 0 \\ 7 \end{pmatrix} + (-7) \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ -7 \\ 0 \end{pmatrix}</math>. | ||
# Für den Schnittpunkt <math>S_{13}</math> der Geraden <math>g</math> mit der <math>x_1x_3</math>-Ebene setze die <math>x_2</math>-Koordinate <math>= 0</math> und forme nach <math>r</math> um: <math>0 = r</math>. Setze nun <math>r = 0</math> in der Geradengleichung ein, um den Schnittpunkt <math>S_{13}</math> zu erhalten: <math>\vec{S_{13}} = \begin{pmatrix} 7 \\ 0 \\ 7 \end{pmatrix} + 0 \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 7 \\ 0 \\ 7 \end{pmatrix}</math> | |||
# Für den Schnittpunkt <math>S_{23}</math> der Geraden <math>g</math> mit der <math>x_2x_3</math>-Ebene setze die <math>x_1</math>-Koordinate <math>= 0</math> und forme nach <math>r</math> um: <math>0 = 7 + r \cdot 1 \Leftrightarrow r = -7</math>. Setze nun <math>r = -7</math> in der Geradengleichung ein, um den Schnittpunkt <math>S_{12}</math> zu erhalten: <math>\vec{S_{12}} = \begin{pmatrix} 7 \\ 0 \\ 7 \end{pmatrix} + (-7) \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ -7 \\ 0 \end{pmatrix}</math>. Hinweis (war nicht in der Aufgabe gefordert): Man erkennt, dass es sich um den selben Schnittpunkt handelt wie der Schnittpunkt der Gerade mit der <math>x_1x_2</math>-Ebene, also: <math>S_{12} = S_{23}</math>. | |||
|Lösung Aufgabe a) anzeigen | |||
|Lösung Aufgabe a) verbergen | |||
}} | }} | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Schnittpunkt <math>S_{12}</math> der Geraden <math>g</math> mit der <math>x_1x_2</math>-Ebene: <math>\vec{S_{12}} = \begin{pmatrix} 1 \\ - | |# Für den Schnittpunkt <math>S_{12}</math> der Geraden <math>g</math> mit der <math>x_1x_2</math>-Ebene setze die <math>x_3</math>-Koordinate <math>= 0</math> und forme nach <math>r</math> um: <math>0 = 2 + r \cdot 1 \Leftrightarrow r = -2</math>. Setze nun <math>r = -2</math> in der Geradengleichung ein, um den Schnittpunkt <math>S_{12}</math> zu erhalten: <math>\vec{S_{12}} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + (-2) \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ -8 \\ 0 \end{pmatrix}</math>. | ||
# Für den Schnittpunkt <math>S_{13}</math> der Geraden <math>g</math> mit der <math>x_1x_3</math>-Ebene setze die <math>x_2</math>-Koordinate <math>= 0</math> und forme nach <math>r</math> um: <math>0 = -4 + r \cdot 2 \Leftrightarrow r = 2</math>. Setze nun <math>r = 2</math> in der Geradengleichung ein, um den Schnittpunkt <math>S_{13}</math> zu erhalten: <math>\vec{S_{13}} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix}</math> | |||
# Für den Schnittpunkt <math>S_{23}</math> der Geraden <math>g</math> mit der <math>x_2x_3</math>-Ebene setze die <math>x_1</math>-Koordinate <math>= 0</math>: <math>0 = 1 + r \cdot 0 \Leftrightarrow 0 = 1</math>. Es ergibt sich ein Widerspruch, weshalb es keinen Schnittpunkt <math>S_{23}</math> der Geraden <math>g</math> mit der <math>x_2x_3</math>-Ebene gibt. Somit verläuft <math>g</math> parallel zur <math>x_2x_3</math>-Ebene. | |||
|Lösung Aufgabe b) anzeigen | |||
|Lösung Aufgabe b) verbergen | |||
}} | }} | ||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |# Für den Schnittpunkt <math>S_{12}</math> der Geraden <math>g</math> mit der <math>x_1x_2</math>-Ebene setze die <math>x_3</math>-Koordinate <math>= 0</math> und forme nach <math>r</math> um: <math>0 = 4 + r \cdot (-4) \Leftrightarrow r = 1</math>. Setze nun <math>r = 1</math> in der Geradengleichung ein, um den Schnittpunkt <math>S_{12}</math> zu erhalten: <math>\vec{S_{12}} = \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix} + 1 \cdot \begin{pmatrix} 2 \\ 0 \\ -4 \end{pmatrix} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix}</math>. | ||
# Für den Schnittpunkt <math>S_{13}</math> der Geraden <math>g</math> mit der <math>x_1x_3</math>-Ebene setze die <math>x_2</math>-Koordinate <math>= 0</math> und forme nach <math>r</math> um: <math>0 = 0 + r \cdot 0 \Leftrightarrow 0 = 0</math>. Man erhält keine Lösung für den Parameter <math>r</math>, aber auch keinen Widerspruch. Somit hat die Gerade unendlich viele Spurpunkte mit er <math>x_1x_2</math>-Ebene, da sie innerhalb dieser Ebene verläuft. | |||
# Für den Schnittpunkt <math>S_{23}</math> der Geraden <math>g</math> mit der <math>x_2x_3</math>-Ebene setze die <math>x_3</math>-Koordinate <math>= 0</math> und forme nach <math>r</math> um: <math>0 = 1 + r \cdot 2 \Leftrightarrow r = -\frac{1}{2}</math>. Setze nun <math>r = -\frac{1}{2}</math> in der Geradengleichung ein, um den Schnittpunkt <math>S_{23}</math> zu erhalten: <math>\vec{S_{23}} = \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix} + (-\frac{1}{2}) \cdot \begin{pmatrix} 2 \\ 0 \\ -4 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 6 \end{pmatrix}</math>. | |||
|Lösung Aufgabe c) anzeigen | |||
|Lösung Aufgabe c) verbergen | |||
}} | }} | ||
| | |Hervorhebung1 | ||
}} | |||
}} | |||
==Lagebeziehungen von Geraden== | ==Lagebeziehungen von Geraden== | ||
| Zeile 271: | Zeile 418: | ||
====Parallele und identische Geraden==== | ====Parallele und identische Geraden==== | ||
{{Box|1=Infobox zur Lagebeziehung zweier Geraden Teil 1 | {{Box|1=Infobox zur Lagebeziehung zweier Geraden Teil 1 | ||
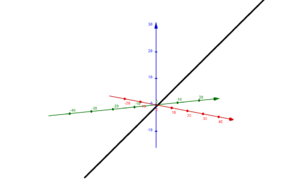
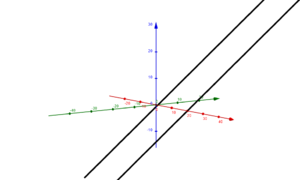
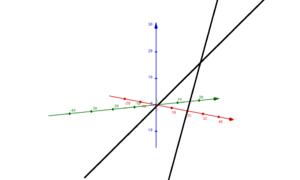
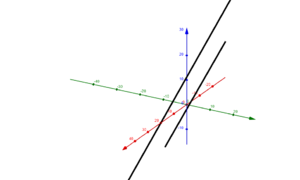
|2=Wir unterscheiden die Lage zweier Geraden in '''identisch''', '''parallel''', '''sich schneidend''' und '''windschief zueinander'''. | |2= Wir unterscheiden die Lage zweier Geraden in '''identisch''', '''parallel''', '''sich schneidend''' und '''windschief zueinander'''. | ||
[[Datei:Zwei identische Geraden.png|links|mini|Zwei identische Geraden]] | [[Datei:Zwei identische Geraden.png|links|mini|Zwei identische Geraden]] | ||
[[Datei:Zwei parallele Geraden.png|rechts|mini|Zwei parallele Geraden]] | [[Datei:Zwei parallele Geraden.png|rechts|mini|Zwei parallele Geraden]] | ||
Um die Lage zweier Geraden zu ermitteln, betrachtet man zunächst die Richtungsvektoren. Sind diese zueinander '''kollinear''' (sind Vielfache voneinander), so können die Geraden lediglich '''identisch''' oder '''parallel''' sein. | |||
Um nun zu untersuchen, ob die Geraden '''parallel''' oder '''identisch''' sind, setzen wir einen Punkt der einen Geraden in die Geradengleichung der anderen Geraden ein. Liegt der Punkt der einen Geraden auf der anderen Geraden, sind die Geraden '''identisch'''. Andernfalls sind die Geraden '''parallel''' zueinander. | Um nun zu untersuchen, ob die Geraden '''parallel''' oder '''identisch''' sind, setzen wir einen Punkt der einen Geraden in die Geradengleichung der anderen Geraden ein. Liegt der Punkt der einen Geraden auf der anderen Geraden, sind die Geraden '''identisch'''. Andernfalls sind die Geraden '''parallel''' zueinander. | ||
| Zeile 295: | Zeile 442: | ||
|3=Merksatz}} | |3=Merksatz}} | ||
{{Box|1= Aufgabe | {{Box|1= Aufgabe 9: Lage erkennen|2=Löse das Quiz und mache dir deinen eigenen Lernzettel. | ||
{{LearningApp|app=19038875|width=100%|height=554px}} | {{LearningApp|app=19038875|width=100%|height=554px}} | ||
| Zeile 301: | Zeile 448: | ||
{{Box|1= Aufgabe | {{Box|1= Aufgabe 10: Lage zweier Geraden|2=Löse den Lückentext und mache dir deinen eigenen Lernzettel. | ||
{{LearningApp|app=19689096|width=100%|height=554px}}|Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | {{LearningApp|app=19689096|width=100%|height=554px}}|Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | ||
{{Box|1= Aufgabe | {{Box|1= Aufgabe 11: Lage erkennen|2= Betrachte die folgenden Geraden <math>g</math> und <math>h</math>. Wie verlaufen die Geraden zueinander. Entscheide ohne Nutzung des GTR. | ||
'''a)''' <math>g \colon \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}</math> und <math>h \colon \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + | '''a)''' <math>g \colon \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}</math> und <math>h \colon \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}, t \in \mathbb{R} </math> | ||
'''b)''' <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R} </math> und <math>h \colon \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} + | '''b)''' <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R} </math> und <math>h \colon \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, t \in \mathbb{R} </math> | ||
'''c)'''<math>g \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 4 \\ 4 \end{pmatrix}, r \in \mathbb{R} </math> und <math>h \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} 4 \\ 5 \\ 3 \end{pmatrix}, | '''c)''' <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 4 \\ 4 \end{pmatrix}, r \in \mathbb{R} </math> und <math>h \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} 4 \\ 5 \\ 3 \end{pmatrix}, t \in \mathbb{R} </math> | ||
{{Lösung versteckt|1= Hier brauchst du kaum rechnen. Schaue dir die Aufpunkte nochmal genau an. |2= Tipp zu c|3= Tipp zu c}} | |||
'''d)''' <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R} </math> und <math>h \colon \vec{x} = \begin{pmatrix} 3 \\ 3 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 4 \\ 3 \end{pmatrix}, t \in \mathbb{R} </math> | |||
'''e)''' <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R} </math> und <math>h \colon \vec{x} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, t \in \mathbb{R} </math> | |||
<math> | {{Lösung versteckt|1= Die erste Antwort lautet ''identisch''. Die beiden Geraden sind ''identisch''. Dies sehen wir daran, dass die Richtungsvekoren mit <math> 2\cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix} </math> ein Vielfaches voneinander (=kollinear) sind. Da beide Stützvektoren identisch sind, weißt du, dass der Punkt <math>(2|2|5)</math> auf beiden Geraden liegt und somit die beiden Geraden ''identisch'' sind.|2=Lösung Aufgabe a |3=Lösung Aufgabe a}} | ||
2= | |||
2 | {{Lösung versteckt|1= Die zweite Antwort lautet ''parallel''. Die beiden Geraden sind ''parallel''. Während die beiden Richtungsvektoren kollinear, sogar identisch, sind liegt der Aufpunkt <math>(2|2|2)</math> von der Gerade <math>h</math> nicht auf der Geraden von <math> g</math> | ||
2=1+r\ | <math> \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}</math>, mit | ||
</math> | |||
<math> | <math>\left\vert\begin{alignat}{7} | ||
1 | 2 &&\; = \;&& 1 &&\; +\;&& r\cdot1\\ | ||
1 | 2 &&\; =\;&& 1 &&\; +\;&& r\cdot2\\ | ||
1 | 2 &&\; =\;&& 1 &&\; +\;&& r\cdot3 | ||
\end{alignat}\right\vert</math> | |||
Formen wir dies um zu r erhalten wir | |||
<math>\left\vert\begin{alignat}{7} | |||
1 &&\; = \;&& r\cdot1\\ | |||
1 &&\; =\;&& r\cdot2\\ | |||
1 &&\; =\;&& r\cdot3 | |||
\end{alignat}\right\vert</math> | |||
Formen wir weiter zu <math>r</math> um, erhalten wir | |||
<math>\left\vert\begin{alignat}{7} | |||
1 &&\; = \;&& r\\ | |||
0.5 &&\; =\;&& r\\ | |||
0.333 &&\; =\;&& r | |||
\end{alignat}\right\vert</math> | |||
und damit liegt der Punkt nicht auf der Geraden.|2=Lösung Aufgabe b|3=Lösung Aufgabe b}} | |||
{{Lösung versteckt|1= Die dritte Antwort lautet ''schneiden''. Die Richtungsvektoren sind nicht kollinear und damit ''schneiden'' sich die beiden Geraden im Aufpunkt <math>(1|2|3)</math> selbst.|2=Lösung Aufgabe c|3=Lösung Aufgabe c}} | |||
{{Lösung versteckt|1= Die vierte Antwort lautet ''windschief''. Die beiden Geraden sind ''windschief'' zueinander. Dies kannst du wie folgt berechnen. | |||
<math> | <math>\left\vert\begin{alignat}{7} | ||
r\ | 1 &&\; +\;&& r\cdot1 &&\; =\;&& 3 &&\; +\;&& t\cdot1\\ | ||
1 &&\; +\;&& r\cdot2 &&\; =\;&& 3 &&\; +\;&& t\cdot4\\ | |||
r\ | |||
1 &&\; +\;&& r\cdot3 &&\; =\;&& 4 &&\; +\;&& t\cdot3 | |||
\end{alignat}\right\vert</math> | |||
Dies formen wir um: | Dies formen wir um: | ||
<math>\left\vert\begin{alignat}{7} | |||
r\cdot1 &&\; -\;&& t\cdot1 &&\; = \;&& 2 \\ | |||
r\cdot2 &&\; -\;&& t\cdot4 &&\; = \;&& 2 \\ | |||
r\ | |||
r\cdot3 &&\; -\;&& t\cdot3 &&\; = \;&& 3 | |||
r\ | \end{alignat}\right\vert</math> | ||
Wenn die erste Zeile mit <math>2</math> multipliziert wird | Wenn die erste Zeile mit <math>2</math> multipliziert wird | ||
<math>\left\vert\begin{alignat}{7} | |||
r\cdot2 &&\; -\;&& t\cdot2 &&\; = \;&& 4 \\ | |||
r\cdot2 &&\; -\;&& t\cdot4 &&\; = \;&& 2 \\ | |||
r\cdot2-t\ | |||
r\cdot3 &&\; -\;&& t\cdot3 &&\; = \;&& 3 | |||
r\ | \end{alignat}\right\vert</math> | ||
und dann von der ersten Zeile die zweite Zeile subtrahiert wird, | |||
<math>\left\vert\begin{alignat}{7} | |||
t\cdot2 &&\; =\;&& 2 \\ | |||
r\cdot2 &&\; -\;&& t\cdot4 &&\; =\;&& 2 \\ | |||
t\ | |||
r\cdot3 &&\; -\;&& t\cdot3 &&\; =\;&& 3 | |||
r\ | \end{alignat}\right\vert</math> | ||
erhälst du <math>t=1</math>. Wenn du dies in die zweite Zeile einsetzt, erhälst du für <math>r=3</math>. Setzt du dies in die letzte Zeile ein, erhälst du <math>6=3</math>, eine falsche Aussage. Damit sind die beiden Geraden windschief zueinander. | erhälst du <math>t=1</math>. Wenn du dies in die zweite Zeile einsetzt, erhälst du für <math>r=3</math>. Setzt du dies in die letzte Zeile ein, erhälst du <math>6=3</math>, eine falsche Aussage. Damit sind die beiden Geraden windschief zueinander. | ||
|2=Lösung Aufgabe d|3=Lösung Aufgabe d}} | |||
{{Lösung versteckt|1= Die fünfte Antwort lautet ''identisch''. Die beiden Geraden sind identisch. Dies sehen wir daran, dass die Richtungsvekoren identisch sind (<math>\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}</math>) und der Aufpunkt <math>(2|3|4)</math> der Geraden <math>h</math> auf der Geraden <math>g</math> liegt: <math>\begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix}= \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + 1 \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}</math>. |2=Lösung Aufgabe e|3=Lösung Aufgabe e}} | |||
|Farbe={{Farbe|orange}}|3= Arbeitsmethode }} | |||
{{Box|1= Aufgabe | {{Box|1= Aufgabe 12: Flugerlaubnis erteilen?|2= | ||
Ein wichtiger Bestandteil der Flugsicherung sind die Fluglotsen der "Deutschen Flugsicherung" (DFS). Sie koordinieren und überwachen jährlich Millionen Flüge im deutschen Luftraum. | Ein wichtiger Bestandteil der Flugsicherung sind die Fluglotsen der "Deutschen Flugsicherung" (DFS). Sie koordinieren und überwachen jährlich Millionen Flüge im deutschen Luftraum. Fluglotsenschüler Karl überwacht gerade zwei Flugzeuge. Hierzu gehört das Flugzeug der Fluglinie Aer. Es befindet sich bei <math> \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix}</math> und fliegt innerhalb von 5 Sekunden zum Punkt <math> \begin{pmatrix} 510 \\ 410 \\ 350 \end{pmatrix}</math>. Ebenfalls ist das Flugzeug der Fluglinie Amadeus in die Luft. Dies befindet sich in <math> \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix}</math>. Pro Sekunde legt es eine Strecke von <math>175{,}49</math> m zurück und besitzt einen Richtungsvektor von <math> \begin{pmatrix} 120{,}2 \\ 96{,}4 \\ z \end{pmatrix}</math>. | ||
Es kam zu einem riesigen Stromausfall und der Fluglotse ist sich unsicher. Hilf ihm die Antworten auf folgende Fragen zu finden: | Es kam zu einem riesigen Stromausfall und der Fluglotse ist sich unsicher, ob die beiden Flugzeuge ohne Probleme weiterfliegen können oder kollidieren. Hilf ihm die Antworten auf folgende Fragen zu finden: | ||
'''a)''' Wie lauten die Geradengleichungen der einzelen Flugzeuge? | '''a)''' Wie lauten die Geradengleichungen der einzelen Flugzeuge? | ||
| Zeile 475: | Zeile 574: | ||
{{Lösung versteckt|1= Geschwindigkeit kann in verschiedene Einheiten angegeben werden, z.B.: <math>\tfrac{km}{h}</math>, <math>\tfrac{m}{s}</math> etc.. Nachdem du die Länge der Strecke nach einer Sekunde berechnet hast, musst du dies von <math>\tfrac{m}{s}</math> zu <math>\tfrac{km}{h}</math> umwandeln.|2=Tipp zu b |3=Tipp zu b}} | {{Lösung versteckt|1= Geschwindigkeit kann in verschiedene Einheiten angegeben werden, z.B.: <math>\tfrac{km}{h}</math>, <math>\tfrac{m}{s}</math> etc.. Nachdem du die Länge der Strecke nach einer Sekunde berechnet hast, musst du dies von <math>\tfrac{m}{s}</math> zu <math>\tfrac{km}{h}</math> umwandeln.|2=Tipp zu b |3=Tipp zu b}} | ||
'''c)''' Können alle Flugzeuge | Die Batterien deines GTRs haben den Geist aufgegeben. Es ist immer noch kein Strom vorhanden und der Fluglotse stellt dir die alles entscheidene Frage: | ||
'''c)''' Können alle Flugzeuge weiterfliegen, ohne dass es zu einer Kollision kommt? | |||
{{Lösung versteckt|1= Nur weil sich zwei Geraden schneiden heißt es noch nicht direkt, dass eine Kollision vorherrscht.|2=Tipp zu c |3=Tipp zu c}} | {{Lösung versteckt|1= Nur weil sich zwei Geraden schneiden heißt es noch nicht direkt, dass eine Kollision vorherrscht.|2=Tipp zu c |3=Tipp zu c}} | ||
| Zeile 489: | Zeile 590: | ||
<math>\begin{pmatrix} 510 \\ 410 \\ 350 \end{pmatrix} = \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + 5\cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix}, t \in \mathbb{R} </math>. Dies musst du in ein Gleichugssystem umformen und dies dann zu <math>x</math>,<math>y</math> und <math>z</math> auflösen: | <math>\begin{pmatrix} 510 \\ 410 \\ 350 \end{pmatrix} = \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + 5\cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix}, t \in \mathbb{R} </math>. Dies musst du in ein Gleichugssystem umformen und dies dann zu <math>x</math>,<math>y</math> und <math>z</math> auflösen: | ||
<math> | <math>\left\vert\begin{alignat}{7} | ||
510=10+5\cdot x </math> | 510 &&\; =\;&& 10 &&\; +\;&& 5\cdot x\\ | ||
410 &&\; =\;&& 10 &&\; +\;&& 5\cdot y\\ | |||
350 &&\; =\;&& 0 &&\; +\;&& 5\cdot z | |||
\end{alignat}\right\vert</math> | |||
Zunächst bringst du die Zahlen auf die andere Seite: | Zunächst bringst du die Zahlen auf die andere Seite: | ||
<math>\left\vert\begin{alignat}{7} | |||
500 &&\; =\;&& 5\cdot x\\ | |||
400 &&\; =\;&& 5\cdot y\\ | |||
350 &&\; =\;&& 5\cdot z | |||
\end{alignat}\right\vert</math> | |||
<math> | und formst dann zu <math>x</math>,<math>y</math> und <math>z</math> um: | ||
<math>\left\vert\begin{alignat}{7} | |||
100 &&\; =\;&& x\\ | |||
80 &&\; =\;&& y\\ | |||
70 &&\; =\;&& z | |||
\end{alignat}\right\vert</math> | |||
Und erhälst damit direkt den Richtungsvektor. | |||
Flugzeug Amadeus: | Flugzeug Amadeus: | ||
| Zeile 526: | Zeile 626: | ||
Dies erhälst du wie folgt: | Dies erhälst du wie folgt: | ||
Du kennst den Richtungsvektor: | Du kennst den Richtungsvektor: | ||
<math> \begin{pmatrix} 120{,}2\\ 96{,}4 \\ | <math> \begin{pmatrix} 120{,}2\\ 96{,}4 \\ z\end{pmatrix}</math>. Nun musst du <math>z</math> berechnen. Im Text steht, dass das Flugzeug pro Sekunde eine Strecke von <math>175{,}49</math> m fliegt. Das bedeutet, dass der Richtungsvektor eine Länge von <math>175{,}49</math> besitzt. Dies kannst du mit der Formel der Länge eines Vektor berechnen: | ||
| Zeile 532: | Zeile 632: | ||
Indem du beide Seiten zum | Indem du beide Seiten zum Quadart nimmst, entfällt die Wurzel und es folgt: | ||
| Zeile 538: | Zeile 638: | ||
Du formst zu <math>z^{2}</math> um und ziehst dann die Wurzel. Du erhälst gerundet <math>84</math>. | Du formst zu <math>z^{2}</math> um und ziehst dann die Wurzel. Du erhälst gerundet <math>84</math> und <math>-84</math>. Da es sich hier jedoch nicht um ein U-Boot handelt, welches abtaucht, sondern um ein Flugzeug, welches in die Höhe geht, ist hier <math>84</math> die einzig mögliche Antwort. | ||
|2=Lösung Aufgabe a|3=Lösung Aufgabe a}} | |2=Lösung Aufgabe a|3=Lösung Aufgabe a}} | ||
| Zeile 551: | Zeile 651: | ||
<math> L=145{,}95</math>. | <math> L=145{,}95</math>. | ||
Du erhälst also eine Geschwindigkeit von <math>145{,}95</math> <math>\tfrac{m}{s}</math>. Es gilt: <math>3{,}6</math> <math>\tfrac{km}{h}</math>=1 <math>\tfrac{m}{s}</math>. | Du erhälst also eine Geschwindigkeit von <math>145{,}95</math> <math>\tfrac{m}{s}</math>. Es gilt: <math>3{,}6</math> <math>\tfrac{km}{h}</math><math>=1</math> <math>\tfrac{m}{s}</math>. | ||
Umgerechnet in <math>\tfrac{km}{h}</math> sind das also: | Umgerechnet in <math>\tfrac{km}{h}</math> sind das also: | ||
| Zeile 570: | Zeile 670: | ||
Flugzeug Aer und Amadeus: | Flugzeug Aer und Amadeus: | ||
Sie schneiden sich für | Sie schneiden sich für | ||
<math> \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + 30 \cdot \begin{pmatrix} 100 \\ 80 \\ 70 \end{pmatrix}= \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} + 25 \cdot \begin{pmatrix} 120{,}2\\ 96{,}4 \\ 84\end{pmatrix}</math>. Dies | <math> \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + 30 \cdot \begin{pmatrix} 100 \\ 80 \\ 70 \end{pmatrix}= \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} + 25 \cdot \begin{pmatrix} 120{,}2\\ 96{,}4 \\ 84\end{pmatrix}</math>. | ||
Dies erhälst du, wenn du mit dem GTR die beiden Geraden geleichsetzt. Alternativ wollen wir dir hier noch einmal Lösung ohne GTR zeigen. | |||
Du erhälst die Lösung, indem dubeide Funktionen gleichsetzen und in ein Gleichungssystem umformen: | |||
<math>\left\vert\begin{alignat}{7} | |||
10 &&\; +\;&& t\cdot100 &&\; =\;&& 5 &&\; +\;&& s\cdot120{,}2\\ | |||
10 &&\; +\;&& t\cdot80 &&\; =\;&& 0 &&\; +\;&& s\cdot96{,}4\\ | |||
10+t \ | |||
0 &&\; +\;&& t\cdot70 &&\; =\;&& 0 &&\; +\;&& s\cdot84 | |||
\end{alignat}\right\vert</math> | |||
Dann formst du dieses so um, dass alle Zahlen auf einer Seite sind: | |||
<math> | <math>\left\vert\begin{alignat}{7} | ||
5=s \cdot120{,}2-t \cdot100 | 5 &&\; =\;&& s\cdot120{,}2 &&\; -\;&& t\cdot100 \\ | ||
10 &&\; =\;&& s\cdot96{,}4 &&\; -\;&& t\cdot80\\ | |||
10=s \cdot96{,}4 -t \cdot80 | |||
0 &&\; =\;&& s\cdot84 &&\; -\;&& t\cdot70 | |||
0=s \cdot84 -t \cdot70</math> | \end{alignat}\right\vert</math> | ||
und du multiplizierst die erste Zeile mit <math>4</math>, die zweite Zeile mit <math>5</math>: | und du multiplizierst die erste Zeile mit <math>4</math>, die zweite Zeile mit <math>5</math>: | ||
<math>\left\vert\begin{alignat}{7} | |||
20 &&\; = \;&& s\cdot480{,}8 &&\; -\;&& t\cdot400 \\ | |||
50 &&\; =\;&& s\cdot482 &&\; -\;&& t\cdot400\\ | |||
0 &&\; =\;&& s\cdot84 &&\; -\;&& t\cdot70 | |||
\end{alignat}\right\vert</math> | |||
Nun subtrahiere die zweite Zeile von der ersten Zeile: | Nun subtrahiere die zweite Zeile von der ersten Zeile: | ||
<math>\left\vert\begin{alignat}{7} | |||
{-}30 &&\; = \;&& s\cdot{-}1{,}2 \\ | |||
50 &&\; =\;&& s\cdot482 &&\; -\;&& t\cdot400\\ | |||
0 &&\; =\;&& s\cdot84 &&\; -\;&& t\cdot70 | |||
\end{alignat}\right\vert</math> | |||
also folgt: | also folgt: | ||
<math> | <math>\left\vert\begin{alignat}{7} | ||
25=s | 25 &&\; = \;&& s \\ | ||
50 &&\; =\;&& s\cdot482 &&\; -\;&& t\cdot400\\ | |||
0 &&\; =\;&& s\cdot84 &&\; -\;&& t\cdot70 | |||
\end{alignat}\right\vert</math> | |||
Du erhälst also <math>s=25 </math>. Wenn du dies in die zweite Zeile einsetzt und umformst, erhälst du: | Du erhälst also <math>s=25 </math>. Wenn du dies in die zweite Zeile einsetzt und umformst, erhälst du: | ||
<math> | <math>\left\vert\begin{alignat}{7} | ||
25=s | 25 &&\; = \;&& s \\ | ||
30 &&\; =\;&& t \\ | |||
0 &&\; =\;&& 25\cdot84 &&\; -\;&& t\cdot70 | |||
\end{alignat}\right\vert</math> | |||
Setzen wir nun in die letzte Zeile <math>t=30</math> ein, so erhalten wir dort <math>0=0</math> und wissen damit, dass sich die Geraden schneiden. | Setzen wir nun in die letzte Zeile <math>t=30</math> ein, so erhalten wir dort <math>0=0</math> und wissen damit, dass sich die Geraden schneiden. | ||
| Zeile 648: | Zeile 746: | ||
|Farbe={{Farbe|grün}}|3= Arbeitsmethode}} | |Farbe={{Farbe|grün}}|3= Arbeitsmethode}} | ||
== | {{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Unterwegs_in_3-D_–_Punkte,_Vektoren,_Geraden_und_Ebenen_im_Raum#Kapitelauswahl}} | ||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 23. Juni 2021, 17:42 Uhr
Geraden und ihre Darstellungsformen
Parameterdarstellung einer Geraden
Wie du nun eine Parametergleichung durch zwei gegebene Punkte aufstellst, wird im folgenden Video erklärt:
Du kannst aber auch eine Gerade aufstellen, die durch einen Punkt verläuft und parallel zu einer anderen Gerade oder zu einer der Koordinatenachsen ist.
Punktprobe
Wie du überprüfst, ob ein gegebener Punkt auf einer gegebenen Gerade oder daneben liegt, kannst du hier noch einmal nachschauen.
Hier noch eine Aufgabe zu Geraden mit besonderen Lagen im Koordinatensystem:
Spurpunkte einer Geraden
Wie du die Spurpunkte, also die Schnittpunkte der Geraden mit den Koordinatenebenen bestimmst, kannst du hier noch einmal nachvollziehen:
Falls du nicht mehr weißt, was die Koordinatenebenen sind, kannst unter folgendem Tipp noch einmal dein Wissen auffrischen:
Die -Ebene ist die Ebene, die von der - und -Achse aufgespannt wird (im Bild genannt). Entsprechendes gilt für die - (im Bild ) und -Ebene (im Bild ).
Lagebeziehungen von Geraden
Parallele und identische Geraden