Benutzer:Georg WWU-8/Testseite2: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Punkte und Vektoren== | ==Punkte und Vektoren== | ||
{{Box|1= Übung 1: Koordinatensysteme|2= Für diese Aufgabe benötigst du einen Bleistift, ein kariertes Blatt Papier und ein Geodreieck. Bearbeite die folgenden Aufgaben. | |||
# Zeichne ein dreidimensionales Koordinatensystem. Wähle eine passende Skalierung anhand der angegebenen Punkte im Aufgabenteil 2 und 3. | |||
# Zeichne die Punkte <math> A (1|2|1)</math>,<math> B(1|4|2)</math>, <math> C(1|2|-1,5)</math> und <math> D(1|4|-0,5) </math> in das gezeichnete Koordinatensystem. Handelt es sich um eine Figur oder um einen Körper? Benenne den Körper. | |||
# Nutze den Punkt <math> A (1|2|1)</math> aus Aufgabenteil 2. Füge die Punkte <math> E (-1|2|1)</math>,<math> F(1|0|1)</math>, <math> G(-1|0|1)</math> und <math> H(0|1|5) </math>. Handelt es sich um eine Figur oder um einen Körper? | |||
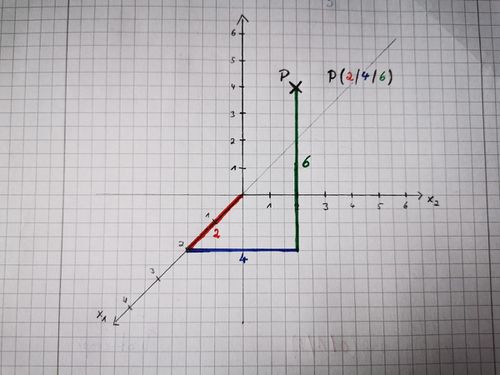
{{Lösung versteckt|1= Punkte in einem dreidimensionalen Koordinatensystem kannst du mithilfe eines "Pfad-Folge-Verfahren" genau bestimmen. Dabei geht man die durch die Punktkoordinaten angegeben Längeneinheiten in die Richtung der jeweiligen Achsen. Das folgende Bild verdeutlicht das Verfahren. | |||
[[Datei:Punkte im dreidimensionalen Koordinatensystem.jpg|rahmenlos|500x500px|Pfad-Folge-Verfahren]] |2= Tipp|3=Einklappen}} | |||
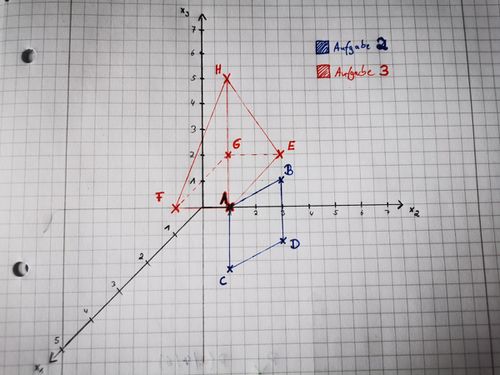
{{Lösung versteckt|1= Bei Aufgabe 2 handelt es sich um ein Parallelogram. Bei Aufgabe 3 bekommst du eine Pyramide heraus, die eine quadratische Grundfläche besitzt. Deine Lösung kann aufgrund einer anderen Skalierung der Achsen natürlich auch von folgenden Lösung abweichen. | |||
[[Datei:Lösung Aufgabe 1-2-3.jpg|rahmenlos|500x500px|Lösung]] |2= Lösung|3=Einklappen}} | |||
|Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | |||
{{Box|1= Übung 2: Punkte im Koordinatensystem|2= Der angegebene Tetraeder hat eine Höhe von 4 Skalierungseinheiten. An welchen Koordinaten befinden sich die Ecken des Tetraeders? Wähle eine richtige Lösung für jeden Punkt aus. | {{Box|1= Übung 2: Punkte im Koordinatensystem|2= Der angegebene Tetraeder hat eine Höhe von 4 Skalierungseinheiten. An welchen Koordinaten befinden sich die Ecken des Tetraeders? Wähle eine richtige Lösung für jeden Punkt aus. | ||
| Zeile 8: | Zeile 22: | ||
|Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | |Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | ||
{{Box|1= Übung 3: Geometrische Objekte im Koordinatensystem|2= Die abgebildete Pyramide besitzt einen einen Eckpunkt im Nullpunkt | {{Box|1= Übung 3: Geometrische Objekte im Koordinatensystem|2= Die abgebildete Pyramide besitzt einen einen Eckpunkt im Nullpunkt <math> A(0|0|0)</math>. Welche Aussagen stimmen mit den abgebildeten Punkten überein? [[Datei:PyramideimKS.png|rahmenlos|400x400px|Pyramide mit Grundfläche <math> ABCD </math> und Scheitelpunkt <math> S </math>]] | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{Welche Aussage stimmt für die Koordinaten der Punkte <math> B </math>,<math> | {Welche Aussage stimmt für die Koordinaten der Punkte <math> B </math>,<math> C </math> und <math> D </math> ?} | ||
- <math> B (5|0|0),C(0|0|5),D(0|5|0) </math> | - <math> B (5|0|0),C(0|0|5),D(0|5|0) </math> | ||
- <math> B(0|5|0),C(0|5|5),D(0|0|5) </math> | - <math> B(0|5|0),C(0|5|5),D(0|0|5) </math> | ||
| Zeile 37: | Zeile 51: | ||
|Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | |Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | ||
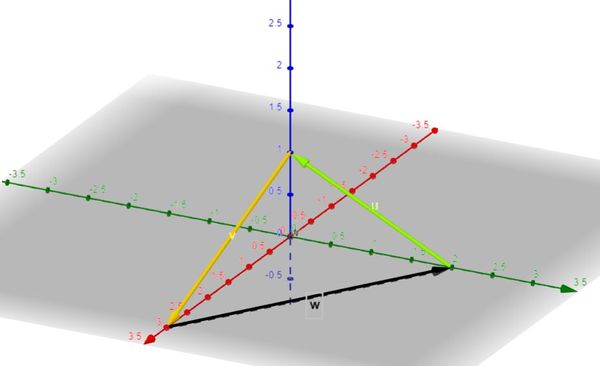
{{Box|1= Übung 4: Vektoren|2= Betrachte die dargestellten Vektoren <math>\vec{u} = \begin{pmatrix} 0 \\ -2 \\ 1 \end{pmatrix} </math>, <math>\vec{v} = \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix}</math> und <math>\vec{w} = \begin{pmatrix} -3 \\ 2 \\ 0 \end{pmatrix}</math>. | |||
[[Datei:Vektoren.jpg|rahmenlos|600x600px]] | |||
Für den Punkt <math> \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}</math> gilt | |||
<math>\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} + \vec{v} + \vec{u} + \vec{w}</math>. | |||
Welche Punkte erhältst du bei folgenden Verschiebungen durch die Vektoren. | |||
# <math>\begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix} + \vec{w} </math> | |||
# <math>\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} - \vec{u} </math> | |||
# <math>\begin{pmatrix} -3 \\ 0 \\ 0 \end{pmatrix} - \vec{w} </math> | |||
# <math>\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} - \vec{u}-\vec{w}-\vec{v} </math> | |||
# <math>\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \vec{v} + \vec{w}+ \vec{u}</math> | |||
# <math>\begin{pmatrix} 0,5 \\ 2 \\ 1 \end{pmatrix} + \vec{w} + \vec{u} +\vec{v} </math> | |||
# <math>\begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} + \vec{u} - \vec{w}</math> | |||
# <math>\begin{pmatrix} -1 \\ 2 \\ -1\end{pmatrix} + \vec{v} - \vec{v}</math> | |||
# <math>\begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} + \vec{u} - \vec{v} - \vec{w}</math> | |||
# <math>\begin{pmatrix} 1 \\ 4 \\ -1 \end{pmatrix} + 2* \vec{u} </math> | |||
{{Lösung versteckt|1= | |||
# <math>\begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} </math> | |||
# <math>\begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} </math> | |||
# <math>\begin{pmatrix} 0 \\ -2 \\ 0 \end{pmatrix} </math> | |||
# <math>\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} </math> | |||
# <math>\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} </math> | |||
# <math>\begin{pmatrix} 0,5 \\ 2 \\ 1 \end{pmatrix} </math> | |||
# <math>\begin{pmatrix} 4 \\ -2 \\ 1 \end{pmatrix} </math> | |||
# <math>\begin{pmatrix} -1 \\ 2 \\ -1 \end{pmatrix} </math> | |||
# <math>\begin{pmatrix} 1 \\ -2 \\ 2 \end{pmatrix} </math> | |||
# <math>\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} </math> | |||
|2= Lösung|3=Einklappen}} | |||
|Farbe={{Farbe|orange}}|3= Arbeitsmethode}} | |||
Aktuelle Version vom 30. April 2021, 13:08 Uhr
Punkte und Vektoren
Spielwiese
Schreiben im Wiki
Neben normalen Text kann auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Vorlagen // Aufträge, Tipps und Hervorhebungen
Das ist ein Tipp.
Das ist eine Lösung
Dateien
Über die Bedienelemente
Mittels Quelltexteingabe (Ohne Umfließen des Textes)
Über Wikipedia (Ohne Rahmen)
Interaktive Applets
LearningApp
GeoGebra