Benutzer:Lena H. WWU-5/Zuordnungen darstellen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box|Einleitung|In diesem Kapitel zu Zuordnungen darstellen, hast du die Möglichkeit, dein Wissen zu den verschiedenen Darstellungsformen von Zuordnungen noch einmal zu vertiefen. Dabei hast du die Wahl zwischen verschiedenen Aufgabentypen. Einige Aufgaben sollst du mit Hilfe deines Hefts lösen, andere lassen sich aber auch auf dieser Seite bearbeiten. | {{Box|Einleitung|In diesem Kapitel zu ''Zuordnungen darstellen'', hast du die Möglichkeit, dein Wissen zu den verschiedenen Darstellungsformen von Zuordnungen noch einmal zu vertiefen. Dabei hast du die Wahl zwischen verschiedenen Aufgabentypen. Einige Aufgaben sollst du mit Hilfe deines Hefts lösen, andere lassen sich aber auch auf dieser Seite bearbeiten. <br /> | ||
Außerdem ist dieser Lernpfad dazu gedacht, dass du die Aufgaben alleine ohne Hilfe einer anderen Person lösen sollst. Falls du aber trotzdem einmal nicht weiterwissen solltest, mach dir keine Sorgen, du findest unter | Außerdem ist dieser Lernpfad dazu gedacht, dass du die Aufgaben alleine ohne Hilfe einer anderen Person lösen sollst. Falls du aber trotzdem einmal nicht weiterwissen solltest, mach dir keine Sorgen, du findest unter einigen Aufgabe Tipps, die du anklicken kannst, falls du einmal nicht weiter wissen solltest. In jedem Fall können aber auch eure Unterrichtsmaterialien weiterhelfen.<br /> | ||
Außerdem findest du auch unter jeder Aufgabe, sofern sie keine Selbstkorrektur-Funktion hat, Lösungen, die du anklicken kannst, wenn du deine Aufgaben gelöst hast. | Außerdem findest du auch unter jeder Aufgabe, sofern sie keine Selbstkorrektur-Funktion hat, Lösungen, die du anklicken kannst, wenn du deine Aufgaben gelöst hast. | ||
| Zeile 10: | Zeile 10: | ||
Aufgaben, die ''gelb'' eingefärbt sind, haben eine ''mittlere Schwierigkeit''. | Aufgaben, die ''gelb'' eingefärbt sind, haben eine ''mittlere Schwierigkeit''. | ||
Und Aufgaben, die ''rot'' eingefärbt sind, sind ''Knobelaufgaben''.|Kurzinfo | Und Aufgaben, die ''rot'' eingefärbt sind, sind etwas ''schwerere'' Aufgaben oder ''Knobelaufgaben''. <br /> | ||
Hier gelangst du zu den anderen Unterkapiteln des Lernpfads: <br /> | |||
[[ Benutzer: Lena H. WWU-5/Zuordnungen mit Formeln beschreiben|Zuordnungen mit Formeln beschreiben]]<br /> | |||
[[ Benutzer: Lena H. WWU-5/Proportionale Zuordnungen| Proportionale Zuordnungen]]|Kurzinfo | |||
}} | }} | ||
<br /> | <br /> | ||
{{Box|1=<span style="color: green"> Aufgabe 1: Eigenschaften einer Zuordnung </span>|2=Fülle den Lückentext aus. | {{Box|1=<span style="color: green"> Aufgabe 1: Eigenschaften einer Zuordnung </span>|2=Fülle den Lückentext aus. | ||
Wenn du alle Lücken ausgefüllt hast, hast du die Möglichkeit, deine Aufgaben mit Hilfe des Häkchens zu überprüfen. | |||
Falls du eine Lücke falsch ausgefüllt haben solltest, kannst du diese ganz einfach korrigieren, indem du eine neue Antwort eintippst. | |||
Falls du eine Lücke falsch ausgefüllt haben solltest, kannst du diese ganz einfach korrigieren, indem du | |||
<br /> | <br /> | ||
Der richtig ausgefüllte Lückentext, kann dir bei den weiteren Aufgaben behilflich sein. | Der richtig ausgefüllte Lückentext, kann dir bei den weiteren Aufgaben behilflich sein. | ||
| Zeile 66: | Zeile 68: | ||
{{Box|1= <span style="color: orange">Aufgabe 3: </span>|2= Eine Schnecke möchte eine 10m hohe Mauer hinaufkriechen. | {{Box|1= <span style="color: orange">Aufgabe 3: </span>|2= Eine Schnecke möchte eine 10m hohe Mauer hinaufkriechen. | ||
<br /> | <br /> | ||
In | In zwei Stunden schafft sie 4m. Da sie das aber so angestrengt hat, muss sie sich erst einmal wieder eine Stunde ausruhen, dabei schafft sie es nicht richtig sich festzuhalten und rutscht deswegen wieder 2m nach unten. Nach der Pause kriecht sie in ihrem Tempo vom Anfang weiter, das heißt, sie schafft wieder 4m in 2 Stunden. | ||
<br /> | <br /> | ||
a) Wie lautet die Zuordnung? Was ist die unabhängige, was ist die abhängige Größe? | a) Wie lautet die Zuordnung? Was ist die unabhängige, was ist die abhängige Größe? | ||
<br /> | |||
{{Lösung versteckt|1= Zeit (in h) → Höhe der Schnecke (in m) oder Entfernung zum Boden (in m) | |||
<br /> | |||
unabhängige Größe: Zeit (in h) | |||
<br /> | |||
abhängige Größe: Höhe der Schnecke (in m) |2=Lösung zu a)|3=schließen}} | |||
<br /> | <br /> | ||
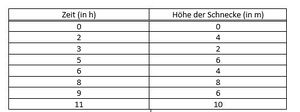
b) Erstelle eine Wertetabelle und einen Graphen zu dieser Zuordnung. | b) Erstelle eine Wertetabelle und einen Graphen zu dieser Zuordnung. | ||
<br /> | <br /> | ||
{{Lösung versteckt|1= | |||
Überlege, wo die Schnecke, nach 2 Stunden, nach 3 Stunden, nach 5 Stunden, nach 6 Stunden etc. ist. | |||
|2=Tipp |3=schließen}} | |||
{{Lösung versteckt|1= | |||
Wertetabelle: [[Datei:Tabelle Schnecke.jpg|mini]] | |||
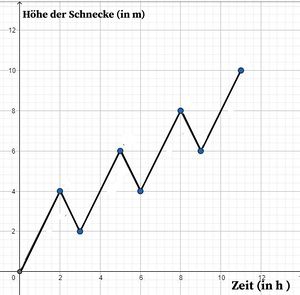
<br /> | |||
Graph: [[Datei:Graph Schnecke.jpg|mini]] | |||
|2=Lösung zu b)|3=schließen}} | |||
c) Wann ist die Schnecke oben angekommen? | c) Wann ist die Schnecke oben angekommen? | ||
<br /> | <br /> | ||
{{Lösung versteckt|1= | |||
Die Schnecke hat nach 11 Stunden die 10m hohe Mauer erklommen. | |||
<br /> |2=Lösung zu c)|3=schließen}} | |||
d) Bestimme zu welchen Zeitpunkten, die Schnecke die Hälfte der 10m erreicht hat. | d) Bestimme zu welchen Zeitpunkten, die Schnecke die Hälfte der 10m erreicht hat. | ||
<br /> | <br /> | ||
{{Lösung versteckt|1= | |||
Die Schnecke hat eine Höhe von 5m jeweils nach 4,5 Stunden, 5,5 Stunden, 6,5 Stunden erreicht. | |||
<br /> |2=Lösung zu d)|3=schließen}} | |||
[[File:Helix pomatia 002.JPG|thumb|Weinbergschnecke (Helix pomatia)|alt=Weinbergschnecke (Helix pomatia)]] | [[File:Helix pomatia 002.JPG|thumb|Weinbergschnecke (Helix pomatia)|alt=Weinbergschnecke (Helix pomatia)]] | ||
<br /> | <br /> | ||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
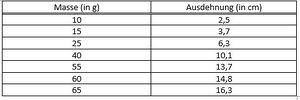
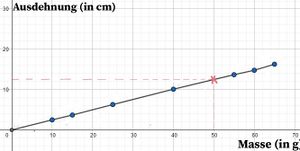
{{Box|1= <span style="color: | {{Box|1= <span style="color: orange">Aufgabe 4: </span>|2= Hängt man Gewichte an eine Feder (wie im Bild), so dehnt sie sich aus. In der folgenden Tabelle sind die Ergebnisse eines Experiments angegeben. | ||
[[File:Ressort de traction à spires jointives.jpg|thumb|Schraubenzugfeder]] | [[File:Ressort de traction à spires jointives.jpg|thumb|Schraubenzugfeder]] | ||
| Zeile 91: | Zeile 119: | ||
<br /> | <br /> | ||
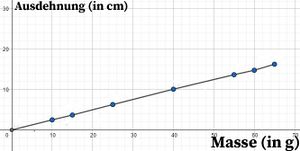
a) Zeichne den Graphen der Zuordnung Masse (in g) → Ausdehnung (in cm). | a) Zeichne den Graphen der Zuordnung ''Masse (in g) → Ausdehnung (in cm)''. | ||
<br /> | <br /> | ||
{{Lösung versteckt|1= | |||
Die unabhängige Größe befindet sich immer auf der x-Achse. | |||
|2=Tipp|3=schließen}} | |||
{{Lösung versteckt|1= | |||
Graph: [[File:Graph zu Federaufgabe.jpg|links|thumb|Graph zu Federaufgabe]] | |||
<br /> |2=Lösung zu a)|3=schließen}} | |||
b) Ermittle, welche Ausdehnung bei einem 50g schweren Gewicht in etwa zu erwarten ist. Erläutere, wie du vorgegangen bist. | b) Ermittle, welche Ausdehnung bei einem 50g schweren Gewicht in etwa zu erwarten ist. Erläutere, wie du vorgegangen bist. | ||
<br /> | |||
{{Lösung versteckt|1= | |||
Versuche mit Hilfe des Graphen herauszufinden, welche y-Koordinate der Punkt auf dem Graphen an der Stelle x=50 hat. | |||
|2=Tipp|3=schließen}} | |||
{{Lösung versteckt|1= | |||
Um herauszufinden, welche Ausdehnung die Feder bei einem Gewicht von 50g hat, legt man das Geodreieck bzw. das Lineal im rechten Winkel an die x-Achse an der Stelle 50. Man zeichnet eine gestrichelte Linie bis diese den Graphen schneidet. Man legt nun das Geodreieck oder Lineal im rechten Winkel an die y-Achse und zeichnet ebenfalls eine gestrichelte Linie, bis zum dem Punkt, an dem die erste gestrichelte Linie auf den Graphen trifft. So findet man die zugehörige y-Koordinate zu x-Koordinate 50. | |||
<br /> | |||
[[Datei:PSX 20201205 140928.jpg|zentriert|mini]] |2=Lösung zu b)|3=schließen}} | |||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
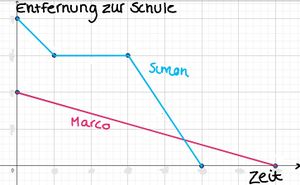
{{Box|1= <span style="color: orange">Aufgabe 5: </span>|2= Simon behauptet gegenüber Marco: "Ich habe dich heute auf dem Schulweg gesehen. Marco ist verwirrt und sagt: "Das versteh ich nicht. Das geht gar nicht, ich bin doch später an der Schule angekommen als du." | {{Box|1= <span style="color: orange">Aufgabe 5: </span>|2= Simon behauptet gegenüber Marco: "Ich habe dich heute auf dem Schulweg gesehen." Marco ist verwirrt und sagt: "Das versteh ich nicht. Das geht gar nicht, ich bin doch später an der Schule angekommen als du." | ||
<br /> | <br /> | ||
a) Du siehst hier den Schulweg von Marco und Simon. Schreibe eine kleine Geschichte, die zu den Graphen passt. | a) Du siehst hier den Schulweg von Marco und Simon. Schreibe eine kleine Geschichte, die zu den Graphen passt. | ||
[[Datei:Graphen Schulweg.jpg|mini]] | [[Datei:Graphen Schulweg.jpg|mini]] | ||
{{Lösung versteckt|1= | |||
Dies ist eine beispielhafte Geschichte, es kann noch viele andere passende Geschichten geben! | |||
Marco geht wie jeden Morgen zu Fuß zur Schule. Das ist für ihn möglich, da sein zu Hause nicht so weit von der Schule weg ist. Auf seinem Schulweg sind keine Kreuzungen oder Ampeln auf die er gegebenenfalls warten müsste. Also kann er ganz in Ruhe in einem gleichmäßigen Tempo zur Schule laufen. | |||
<br /> | <br /> | ||
b) Wer hat denn nun Recht? Stimmt die Aussage von Simon, dass er Marco gesehen hat oder ist dies, wie Marco behauptet gar nicht möglich? Begründe deine Entscheidung anhand der Graphen. | Simon hingegen hat einen längeren Weg weswegen er mit verschiedenen Verkehrsmitteln fahren muss. Die Bushaltestelle befindet sich genau vor seiner Haustür, sodass er quasi direkt in den Bus steigen kann, wenn er das Haus verlässt. Er fährt nur kurz mit diesem Bus und steigt an einer Haltestelle aus, von der er die nächste Straßenbahn nehmen wird. Doch auf die muss er erst einmal ein bisschen warten. Aber einmal in der Straßenbahn dauert es nicht lange bis er direkt vor seiner Schule aussteigen kann. | ||
<br /> |2=Lösung zu a)|3=schließen}} | |||
<br /> | |||
b) Wer hat denn nun Recht? Stimmt die Aussage von Simon, dass er Marco gesehen hat oder ist dies, wie Marco behauptet, gar nicht möglich? Begründe deine Entscheidung anhand der Graphen. | |||
{{Lösung versteckt|1= | |||
Wann & wo muss Simon sich befinden, damit er Marco gesehen haben kann? | |||
|2=Tipp|3=schließen}} | |||
{{Lösung versteckt|1= | |||
Simon hat Recht. Simon kann Marco aus der Straßenbahn beobachten. Das erkennt man an den Graphen an dem Punkt, an dem beide aufeinandertreffen. An diesem Punkt sind Marco und Simon zur gleichen Zeit gleich weit von der Schule entfernt. | |||
<br /> |2=Lösung zu b)|3=schließen}} | |||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
| Zeile 115: | Zeile 172: | ||
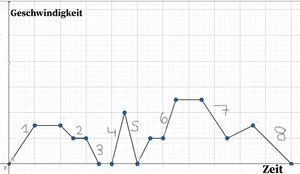
Am Abend möchte Marie ihrer Mutter von den Ereignissen des Tages berichten. Doch leider bringt sie die Dinge immer wieder durcheinander. Hilf Marie die Ereignisse des Tages, passend zum Graphen, in die richtige Reihenfolge zu bringen. | Am Abend möchte Marie ihrer Mutter von den Ereignissen des Tages berichten. Doch leider bringt sie die Dinge immer wieder durcheinander. Hilf Marie die Ereignisse des Tages, passend zum Graphen, in die richtige Reihenfolge zu bringen. | ||
<br /> | <br /> | ||
a. Plötzlich kreuzte ein Fußgänger meinen Weg, deswegen musste ich abbremsen. | <math>a.</math> Plötzlich kreuzte ein Fußgänger meinen Weg, deswegen musste ich abbremsen. | ||
<br /> | <br /> | ||
b. Es gab eine richtig schnelle Abfahrt, danach bin ich erst einmal langsamer gefahren. | <math>b.</math> Es gab eine richtig schnelle Abfahrt, danach bin ich erst einmal langsamer gefahren. | ||
<br /> | <br /> | ||
c. Ich habe meine Freundin Anna getroffen. Sie hat mich freundlicherweise mit dem Fahrrad ein Stück mitgezogen. | <math>c.</math> Ich habe meine Freundin Anna getroffen. Sie hat mich freundlicherweise mit dem Fahrrad ein Stück mitgezogen. | ||
<br /> | <br /> | ||
d. Auf einmal ging es ganz schön bergab. Da musst ich aufpassen, weil ich plötzlich richtig schnell wurde. | <math>d.</math> Auf einmal ging es ganz schön bergab. Da musst ich aufpassen, weil ich plötzlich richtig schnell wurde. | ||
<br /> | <br /> | ||
e. | <math>e.</math> | ||
Erstmal hieß es für mich Schwung holen und Geschwindigkeit aufnehmen. | Erstmal hieß es für mich Schwung holen und Geschwindigkeit aufnehmen. | ||
<br /> | <br /> | ||
f. | <math>f.</math> | ||
Plötzlich gab es auch eine rote Ampel auf meinem Weg. Da musste ich abbremsen und erst einmal warten. | Plötzlich gab es auch eine rote Ampel auf meinem Weg. Da musste ich abbremsen und erst einmal warten. | ||
<br /> | <br /> | ||
g. | <math>g.</math> | ||
Als ich unser Haus sah, fing ich an langsam abzubremsen. | Als ich unser Haus sah, fing ich an langsam abzubremsen. | ||
<br /> | <br /> | ||
h. | <math>h.</math> | ||
Auf einmal tauchte die Polizei vor mir auf. Da musste ich erst einmal scharf abbremsen. | Auf einmal tauchte die Polizei vor mir auf. Da musste ich erst einmal scharf abbremsen. | ||
<br /> | <br /> | ||
{{Lösung versteckt|1= | |||
Überlege dir, zu jedem Ereignis, wie schnell Marie dabei auf ihren Inlinern gefahren ist oder wie sich ihre Geschwindigkeit wegen des Ereignis geändert haben muss. | |||
|2=Tipp|3=schließen}} | |||
{{Lösung versteckt|1= | |||
Die Reihenfolge der Ereignisse ist wie folgt: | |||
<br /> | |||
1. e. | |||
Erstmal hieß es für mich Schwung holen und Geschwindigkeit aufnehmen. | |||
<br /> | |||
2. a. Plötzlich kreuzte ein Fußgänger meinen Weg, deswegen musste ich abbremsen. | |||
<br /> | |||
3. f. | |||
Plötzlich gab es auch eine rote Ampel auf meinem Weg. Da musste ich abbremsen und erst einmal warten. | |||
<br /> | |||
4. d. Auf einmal ging es ganz schön bergab. Da musst ich aufpassen, weil ich plötzlich richtig schnell wurde. | |||
<br /> | |||
5. h. | |||
Auf einmal tauchte die Polizei vor mir auf. Da musste ich erst einmal scharf abbremsen. | |||
<br /> | |||
6. c. Ich habe meine Freundin Anna getroffen. Sie hat mich freundlicherweise mit dem Fahrrad ein Stück mitgezogen. | |||
<br /> | |||
7. b. Es gab eine richtig schnelle Abfahrt, danach bin ich erst einmal langsamer gefahren. | |||
<br /> | |||
8. g. | |||
Als ich unser Haus sah, fing ich an langsam abzubremsen. | |||
<br /> |2=Lösung |3=schließen}} | |||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
Aktuelle Version vom 8. Dezember 2020, 15:01 Uhr