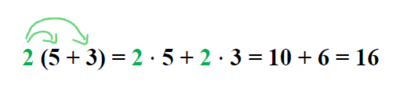Digitale Werkzeuge in der Schule/Fit für VERA-8/Terme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (45 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 46: | Zeile 46: | ||
{{Lösung versteckt| 1= Wenn du dir bei manchen Antworten unsicher bist, schau noch einmal oben in den Rechenregeln nach. | 2= Tipp| 3=Tipp einklappen}}| Arbeitsmethode| Farbe={{Farbe|orange}}}} | {{Lösung versteckt| 1= Wenn du dir bei manchen Antworten unsicher bist, schau noch einmal [[#Einführung|oben]] in den Rechenregeln nach. | 2= Tipp| 3=Tipp einklappen}}| Arbeitsmethode| Farbe={{Farbe|orange}}}} | ||
| Zeile 64: | Zeile 64: | ||
'''b)''' <math> 3x-4y-2z+4y-2x</math> <br/> | '''b)''' <math> 3x-4y-2z+4y-2x</math> <br/> | ||
{{Lösung versteckt| 1= Sortiere zuerst die Variablen, fasse dann gleiche Variablen zusammen. Farbliche Markierungen wie in den Beispielen können dir helfen. | 2=Tipp | 3=Tipp einklappen}} | {{Lösung versteckt| 1= Sortiere zuerst die Variablen, fasse dann gleiche Variablen zusammen. Farbliche Markierungen wie in den [[#Einführung|Beispielen]] können dir helfen. | 2=Tipp | 3=Tipp einklappen}} | ||
{{Lösung versteckt| 1= <math> x+8y-2z </math> | 2= Lösung | 3=Lösung einklappen}} | {{Lösung versteckt| 1= <math> x+8y-2z </math> | 2= Lösung | 3=Lösung einklappen}} | ||
| Zeile 169: | Zeile 169: | ||
|2=Lösung|3=Lösung ausblenden}} | |2=Lösung|3=Lösung ausblenden}} | ||
| 3= Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | 3= Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||
===2) Terme ausmultiplizieren und faktorisieren=== | ===2) Terme ausmultiplizieren und faktorisieren=== | ||
| Zeile 226: | Zeile 225: | ||
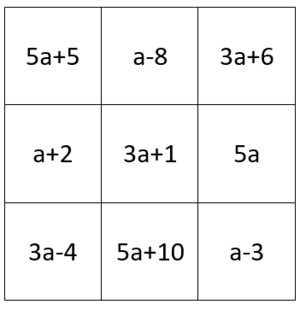
{{Box | 1= Aufgabe 1: Zuordnen | 2= In dieser Aufgabe kannst du das ''Ausmultiplizieren'' üben. Ordne jedem Klammerterm die richtige ausmultiplizierte Lösung zu. Nimm dir einen Zettel für Nebenrechnungen zur Hilfe. | {{Box | 1= Aufgabe 1: Zuordnen | 2= In dieser Aufgabe kannst du das ''Ausmultiplizieren'' üben. Ordne jedem Klammerterm die richtige ausmultiplizierte Lösung zu. Nimm dir einen Zettel für Nebenrechnungen zur Hilfe. | ||
{{Lösung versteckt|1=Schaue dir bei Schwierigkeiten nochmal die Beispiele aus dem Kapitel | {{Lösung versteckt|1=Schaue dir bei Schwierigkeiten nochmal die Beispiele aus dem Kapitel [[#Terme ausmultiplizieren|Terme ausmultiplizieren]] an. | ||
|2=Tipp|3=Verbergen}} | |2=Tipp|3=Verbergen}} | ||
| Zeile 261: | Zeile 260: | ||
=====Aufgabe===== | =====Aufgabe===== | ||
{{Box | 1= Aufgabe 2: Wähle die richtige Antwort | 2= a) Was lässt sich sinnvollerweise ausklammern? | {{Box | 1= Aufgabe 2: Wähle die richtige Antwort | 2= '''a)''' Was lässt sich sinnvollerweise ausklammern? | ||
{{Lösung versteckt|1=Schaue dir (nochmal) die Beispiele aus dem Video von Lehrer Schmidt an. | {{Lösung versteckt|1=Schaue dir (nochmal) die [[#Terme faktorisieren|Beispiele]] aus dem Video von Lehrer Schmidt an. | ||
|2=Tipp|3=Verbergen}} | |2=Tipp|3=Verbergen}} | ||
<br \> | <br \> | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
(i) <math> 9x - 15 </math> (!<math> 5 </math>) (<math> 3 </math>) (!<math> 9 </math>) (!<math> x</math>) <math> </math> | '''(i)''' <math> 9x - 15 </math> (!<math> 5 </math>) (<math> 3 </math>) (!<math> 9 </math>) (!<math> x</math>) <math> </math> | ||
(ii) <math> -36 + 12x </math> (!<math> 9 </math>) (<math> 12 </math>) (!<math> 24 </math>) (!<math> x</math>) | '''(ii)''' <math> -36 + 12x </math> (!<math> 9 </math>) (<math> 12 </math>) (!<math> 24 </math>) (!<math> x</math>) | ||
(iii) <math> 5xy + 4xz + 3x </math> (!<math> 5 </math>) (<math> x </math>) (!<math> y </math>) (!<math> 2z </math>) | '''(iii)''' <math> 5xy + 4xz + 3x </math> (!<math> 5 </math>) (<math> x </math>) (!<math> y </math>) (!<math> 2z </math>) | ||
</div> | </div> | ||
b) Wie sieht der erste Zwischenschritt beim Ausklammern aus? <br \> | '''b)''' Wie sieht der erste Zwischenschritt beim Ausklammern aus? <br \> | ||
{{Lösung versteckt|1=Schaue bei Teilaufgabe | {{Lösung versteckt|1=Schaue bei Teilaufgabe a) nach, was du ausklammerst. | ||
|2=Tipp|3=Verbergen}} | |2=Tipp|3=Verbergen}} | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
(i) <math> 9x - 15 </math> (<math> 3 \cdot 3x - 3 \cdot 5 </math>) (!<math> 3 \cdot 9x - 3 \cdot 5 </math>) (!<math> 3 \cdot 3x + 3 \cdot 5 </math>) (!<math> 3 \cdot x -15 </math>) | '''(i)''' <math> 9x - 15 </math> (<math> 3 \cdot 3x - 3 \cdot 5 </math>) (!<math> 3 \cdot 9x - 3 \cdot 5 </math>) (!<math> 3 \cdot 3x + 3 \cdot 5 </math>) (!<math> 3 \cdot x -15 </math>) | ||
(ii) <math> -36 + 12x </math> (<math> 12 \cdot [-3] + 12 \cdot x </math>) (!<math> 12 \cdot 3 + 12 \cdot x </math>) (!<math> 12 \cdot [-3] - 12 \cdot x </math>) (!<math> 12 \cdot [-3] + x </math>) | '''(ii)''' <math> -36 + 12x </math> (<math> 12 \cdot [-3] + 12 \cdot x </math>) (!<math> 12 \cdot 3 + 12 \cdot x </math>) (!<math> 12 \cdot [-3] - 12 \cdot x </math>) (!<math> 12 \cdot [-3] + x </math>) | ||
</div> | </div> | ||
c) Klammere komplett aus: | '''c)''' Klammere komplett aus: | ||
{{Lösung versteckt|1=Schaue bei Teilaufgabe | {{Lösung versteckt|1=Schaue bei Teilaufgabe a) nach, was du ausklammerst und bei b) wie dein erster Zwischenschritt aussieht. Mache zur Überprüfung die Probe wie es im Kapitel zum [[#Terme faktorisieren|''Faktorisieren'']] erklärt ist. <br /> | ||
Mache zur Überprüfung die Probe wie es im Kapitel zum ''Faktorisieren'' erklärt ist. <br /> | |||
|2=Tipp|3=Verbergen}} | |2=Tipp|3=Verbergen}} | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
(i) <math> 9x - 15 </math> (<math> 3 \cdot [3x - 5] </math>) (!<math> 3 \cdot [9x - 15] </math>) (!<math> 3 \cdot [x - 5] </math>) (!<math> 3 \cdot [3x + 5] </math>) | '''(i)''' <math> 9x - 15 </math> (<math> 3 \cdot [3x - 5] </math>) (!<math> 3 \cdot [9x - 15] </math>) (!<math> 3 \cdot [x - 5] </math>) (!<math> 3 \cdot [3x + 5] </math>) | ||
(ii) <math> -36 + 12x </math> (<math> 12 \cdot [-3 + x] </math>) (!<math> 12 \cdot [3 + x ] </math>) (!<math> 12 \cdot [6 + 3x] </math>) (!<math> 3 \cdot [3 + x] </math>) | '''(ii)''' <math> -36 + 12x </math> (<math> 12 \cdot [-3 + x] </math>) (!<math> 12 \cdot [3 + x ] </math>) (!<math> 12 \cdot [6 + 3x] </math>) (!<math> 3 \cdot [3 + x] </math>) | ||
(iii) <math> 5xy + 4xz + 3x </math> (!<math> x \cdot [54yz + 3]</math>) (<math> x \cdot [5y + 4z + 3] </math>) (!<math> 2x \cdot [5y + 4z + 3]</math>) (!<math> 5 \cdot [xy + 4xz + 3x]</math>) | '''(iii)''' <math> 5xy + 4xz + 3x </math> (!<math> x \cdot [54yz + 3]</math>) (<math> x \cdot [5y + 4z + 3] </math>) (!<math> 2x \cdot [5y + 4z + 3]</math>) (!<math> 5 \cdot [xy + 4xz + 3x]</math>) | ||
</div> | </div> | ||
| 3= Arbeitsmethode | Farbe={{Farbe|orange}} }} | | 3= Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
| Zeile 303: | Zeile 301: | ||
{{Lösung versteckt|1=Klammere die rechte Seite des Terms aus. | {{Lösung versteckt|1=Klammere die rechte Seite des Terms aus. | ||
|2=Tipp 1|3=Verbergen}} | |2=Tipp 1|3=Verbergen}} | ||
{{Lösung versteckt|1=Überlege dir dafür zunächst was du mit <math>2x</math> multiplizieren musst, damit du <math>6x</math> erhältst bzw. was du mit <math>7</math> multiplizieren musst, damit du <math>21</math> erhältst. | {{Lösung versteckt|1=Überlege dir dafür zunächst was du mit <math>2x</math> multiplizieren musst, damit du <math>6x</math> erhältst bzw. was du mit <math>7</math> multiplizieren musst, damit du <math>21</math> erhältst. Mache die Probe, wenn du den Platzhalter ausgefüllt hast. | ||
Mache die Probe, wenn du den Platzhalter ausgefüllt hast. | |||
|2=Tipp 2|3=Verbergen}} <br /> | |2=Tipp 2|3=Verbergen}} <br /> | ||
b) '''15()''' <math> \cdot x + 35 = 5 \cdot (3x + 7) </math> <br /> | b) '''15()''' <math> \cdot x + 35 = 5 \cdot (3x + 7) </math> <br /> | ||
| Zeile 323: | Zeile 320: | ||
| 3=Arbeitsmethode}} | | 3=Arbeitsmethode}} | ||
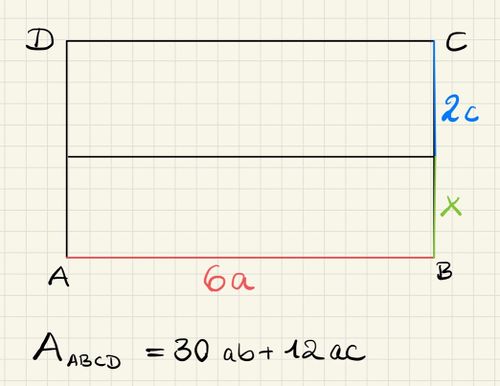
{{Box | 1= Aufgabe 4: Distributivgesetz veranschaulicht | 2= | {{Box | 1= Aufgabe 4: Distributivgesetz veranschaulicht | 2= '''a)''' Wie lang ist die Strecke <math> x </math>?<br /> | ||
[[Datei:Knobel .jpg|500px|links]] <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | [[Datei:Knobel .jpg|500px|links]] <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | ||
{{Lösung versteckt|1=Was kannst du aus dem Term <math> 30ab+12ac </math>, der den Flächeninhalt des Rechtecks beschreibt, ausklammern? | {{Lösung versteckt|1=Was kannst du aus dem Term <math> 30ab+12ac </math>, der den Flächeninhalt des Rechtecks beschreibt, ausklammern? | ||
| Zeile 338: | Zeile 335: | ||
<math> x = </math> '''5b()''' | <math> x = </math> '''5b()''' | ||
</div> | </div> | ||
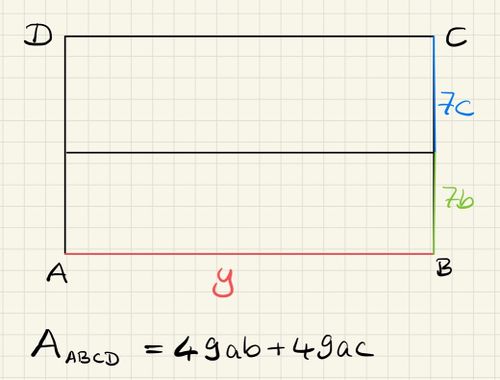
'''b)''' Wie lang ist die Strecke <math> y </math>?<br /> | |||
[[Datei:Knobelaufgabe.jpg|500px|links]] <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | [[Datei:Knobelaufgabe.jpg|500px|links]] <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | ||
{{Lösung versteckt|1=Was kannst du aus dem Term <math> 49ab+49ac </math>, der den Flächeninhalt des Rechtecks beschreibt, ausklammern? | {{Lösung versteckt|1=Was kannst du aus dem Term <math> 49ab+49ac </math>, der den Flächeninhalt des Rechtecks beschreibt, ausklammern? | ||
| Zeile 378: | Zeile 375: | ||
{{Box|1=Beachte|2= | {{Box|1=Beachte|2= | ||
* Bisher hast du lediglich die Herleitung der | * Bisher hast du lediglich die Herleitung der '''1. binomischen Formel''' kennengelernt. Die Herleitungen der '''2. und 3. binomischen Formel''' erfolgen sehr ähnlich und werden hier nicht thematisiert. Falls du dich trotzdem dafür interessierst, schau doch gerne mal bei Serlo vorbei: https://de.serlo.org/mathe/terme-gleichungen/terme-variablen/binomische-formeln | ||
* Die binomischen Formeln werden dir im Laufe deiner Schulzeit immer wieder begegnen, weshalb du sie unbedingt auswendig können solltest. Falls dir dies schwer fällt, schaue dir folgendes Video dazu an. <br \> <br \> <div align="center">{{#ev:youtube|EYbvhWEG6kE}}</div>|3=Merksatz}} | * Die binomischen Formeln werden dir im Laufe deiner Schulzeit immer wieder begegnen, weshalb du sie unbedingt auswendig können solltest. Falls dir dies schwer fällt, schaue dir folgendes Video dazu an. <br \> <br \> <div align="center">{{#ev:youtube|EYbvhWEG6kE}}</div>|3=Merksatz}} | ||
| Zeile 386: | Zeile 383: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Zur Erinnerung: <div align="center">'''1. binomische Formel:''' <math>({\color{green}a}+{\color{blue}b})^2 = {\color{green}a}^2+2{\color{green}a}{\color{blue}b}+{\color{blue}b}^2 </math> </div> <br \> <br \> | Zur Erinnerung: <div align="center">'''1. binomische Formel:''' <math>({\color{green}a}+{\color{blue}b})^2 = {\color{green}a}^2+2{\color{green}a}{\color{blue}b}+{\color{blue}b}^2 </math> </div> <br \> <br \> | ||
Für a und b können verschiedene Zahlen eingesetzt werden: <br \> | Für <math>a</math> und <math>b</math> können verschiedene Zahlen eingesetzt werden: <br \> | ||
a)<math>({\color{green}5}+{\color{blue}3})^2 = {\color{green}5}^2+2 \cdot {\color{green}5} \cdot {\color{blue}3}+{\color{blue}3}^2 = 25+30+9 = 64 (=8^2)</math> <br \> <br \> | a)<math>({\color{green}5}+{\color{blue}3})^2 = {\color{green}5}^2+2 \cdot {\color{green}5} \cdot {\color{blue}3}+{\color{blue}3}^2 = 25+30+9 = 64 (=8^2)</math> <br \> <br \> | ||
Für a und b können auch andere Variablen eingesetzt werden: <br \> | Für <math>a</math> und <math>b</math> können auch andere Variablen eingesetzt werden: <br \> | ||
b)<math>({\color{green}(uv)}+{\color{blue}w})^2 = {\color{green}(uv)}^2+2{\color{green}(uv)}{\color{blue}w}+{\color{blue}w}^2 = u^2v^2+2 \cdot uvw+w^2 </math> <br \> <br \> | b)<math>({\color{green}(uv)}+{\color{blue}w})^2 = {\color{green}(uv)}^2+2{\color{green}(uv)}{\color{blue}w}+{\color{blue}w}^2 = u^2v^2+2 \cdot uvw+w^2 </math> <br \> <br \> | ||
Selbst längere Terme kann man für a und b einsetzen: <br \> | Selbst längere Terme kann man für <math>a</math> und <math>b</math> einsetzen: <br \> | ||
c)<math>({\color{green}(2s+t)}+{\color{blue}u})^2 = {\color{green}(2s+t)}^2+2{\color{green}(2s+t)}{\color{blue}u}+{\color{blue}u}^2 </math> <br \> | c)<math>({\color{green}(2s+t)}+{\color{blue}u})^2 = {\color{green}(2s+t)}^2+2{\color{green}(2s+t)}{\color{blue}u}+{\color{blue}u}^2 </math> <br \> | ||
|2=Beispiele zur 1. binomischen Formel|3=Beispiele ausblenden}} | |2=Beispiele zur 1. binomischen Formel|3=Beispiele ausblenden}} | ||
| Zeile 413: | Zeile 410: | ||
<div class="zuordnungs-quiz"> | <div class="zuordnungs-quiz"> | ||
{{{!}} | {{{!}} | ||
{{!}} 1. binomische Formel {{!}}{{!}} <math forcemathmode="png">(x+19)^2</math> {{!}}{{!}} <math forcemathmode="png">({3\over 4}+p)^2</math> {{!}}{{!}} <math forcemathmode="png">(1,34+\sqrt{5})^2</math> | {{!}} 1. binomische Formel {{!}}{{!}} <math forcemathmode="png">(x+19)^2</math> {{!}}{{!}} <math forcemathmode="png">({3\over 4}+p)^2</math> {{!}}{{!}} <math forcemathmode="png">(1{,}34+\sqrt{5})^2</math> | ||
{{!}}- | {{!}}- | ||
{{!}} 2. binomische Formel {{!}}{{!}} <math forcemathmode="png">(19-x)^2</math> {{!}}{{!}} <math forcemathmode="png">(3-5)^2</math> {{!}}{{!}} <math forcemathmode="png">(25-y)^2</math> | {{!}} 2. binomische Formel {{!}}{{!}} <math forcemathmode="png">(19-x)^2</math> {{!}}{{!}} <math forcemathmode="png">(3-5)^2</math> {{!}}{{!}} <math forcemathmode="png">(25-y)^2</math> | ||
{{!}}- | {{!}}- | ||
{{!}} 3. binomische Formel {{!}}{{!}} <math forcemathmode="png">(5+t)(5-t)</math> {{!}}{{!}} <math forcemathmode="png">({3\over 8}-7)(7+{3\over 8})</math> {{!}}{{!}} <math forcemathmode="png"> (1,37-2)(1,37+2) </math> | {{!}} 3. binomische Formel {{!}}{{!}} <math forcemathmode="png">(5+t)(5-t)</math> {{!}}{{!}} <math forcemathmode="png">({3\over 8}-7)(7+{3\over 8})</math> {{!}}{{!}} <math forcemathmode="png">(1{,}37-2)(1{,}37+2)</math> | ||
{{!}}- | {{!}}- | ||
{{!}} Das ist keine binomische Formel {{!}}{{!}} <math forcemathmode="png">(4+7)(5-7)</math> {{!}}{{!}} <math forcemathmode="png">(5+7)^{1\over 2}</math> {{!}}{{!}} <math forcemathmode="png">s+3^2</math> | {{!}} Das ist keine binomische Formel {{!}}{{!}} <math forcemathmode="png">(4+7)(5-7)</math> {{!}}{{!}} <math forcemathmode="png">(5+7)^{1\over 2}</math> {{!}}{{!}} <math forcemathmode="png">s+3^2</math> | ||
| Zeile 431: | Zeile 428: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
a)<math> 225+30a+a^2 = (</math>'''15()'''<math>+</math>'''a()'''<math>)^2 </math> <br /> | a) <math> 225+30a+a^2 = (</math>'''15()'''<math>+</math>'''a()'''<math>)^2 </math> <br /> | ||
b)<math> 9a^2-16b^2 = (</math>'''3a()'''<math>+</math>'''4b()'''<math>)\cdot ( </math>'''3a()'''<math>-</math>'''4b()''') <br /> | b) <math> 9a^2-16b^2 = (</math>'''3a()'''<math>+</math>'''4b()'''<math>)\cdot ( </math>'''3a()'''<math>-</math>'''4b()''') <br /> | ||
c)<math> 81u^2-36u+4 = (</math>'''9u()'''<math>-</math>'''2()'''<math>)^2 </math> <br /> | c) <math> 81u^2-36u+4 = (</math>'''9u()'''<math>-</math>'''2()'''<math>)^2 </math> <br /> | ||
d)<math> 4m^2+28m+49 = (</math>'''2m()'''<math>+</math>'''7()'''<math>)^2 </math> <br /> | d) <math> 4m^2+28m+49 = (</math>'''2m()'''<math>+</math>'''7()'''<math>)^2 </math> <br /> | ||
e)<math> 64y^2-160yz+100z^2 = (</math>'''8y()'''<math>-</math>'''10z()'''<math>)^2 </math> <br /> | e) <math> 64y^2-160yz+100z^2 = (</math>'''8y()'''<math>-</math>'''10z()'''<math>)^2 </math> <br /> | ||
f)<math> 36u^2-121w^2 = (</math>'''6u()'''<math>+</math>'''11w()'''<math>)\cdot ( </math>'''6u()'''<math>-</math>'''11w()''') <br /> | f) <math> 36u^2-121w^2 = (</math>'''6u()'''<math>+</math>'''11w()'''<math>)\cdot ( </math>'''6u()'''<math>-</math>'''11w()''') <br /> | ||
</div> | </div> | ||
{{Lösung versteckt|1='''Klammere aus'''. Falls du dir unsicher bist, mache die Probe. Du kannst auch [[#Terme faktorisieren|hier]] noch einmal vorbeischauen. | {{Lösung versteckt|1= | ||
Schaue dir auch noch einmal die [[#Was sind die binomischen Formeln?|binomischen Formeln]] an und entscheide, '''wann''' du '''welche''' Formel anwenden kannst.|2=Tipp|3=Tipp ausblenden}} | '''Klammere aus'''. Falls du dir unsicher bist, mache die Probe. Du kannst auch [[#Terme faktorisieren|hier]] noch einmal vorbeischauen. | ||
Schaue dir auch noch einmal die [[#Was sind die binomischen Formeln?|binomischen Formeln]] an und entscheide, '''wann''' du '''welche''' Formel anwenden kannst.|2=Tipp 1|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> 9x^2-6xy+y^2 = (3x-y)^2 </math> | Wir suchen die passende binomische Formel für den Term <math> 9x^2-6xy+y^2 </math>. | ||
Die Anzahl der Summanden bzw. Minuenden geben uns Auskunft darüber, welche binomische Formel wir anwenden können. In diesem Fall haben wir '''zwei Summanden''' und '''einen Minuenden'''. Dies stimmt mit der '''2. binomischen Formel''' überein: <br /> | |||
<div align="center"> <math>(a-b)^2 = a^2-2ab+b^2 </math>. Unsere binomische Formel hat also die Form <math>(a-b)^2 </math>. </div> <br /> | |||
Nun müssen wir noch a und b herausfinden. Wir wissen, dass <math> a^2 = 9x^2 </math> und <math> b^2 = y^2 </math>. | |||
Nun ziehen wir aus diesen Ausdrücken die Wurzel, um a und b zu erhalten: <br /> | |||
<div align="center"> <math> a = \sqrt{a^2} = \sqrt{9x^2} = 3x </math> und <math> b = \sqrt{b^2} = \sqrt{y^2} = y </math>. </div> | |||
Also lautet die binomische Formel <math> (3x-y)^2 </math>. | |||
<br /> <br /> | |||
Probe:<div align="center"> <math> ({\color{green}3x}-{\color{blue}y})^2 = {\color{green}(3x)}^2-2 \cdot {\color{green}3x}{\color{blue}y}+{\color{blue}y}^2 = 9x^2-6xy+y^2 </math>. </div> <br /> | |||
Das Vorgehen für die 1. und 3. binomische Formel erfolgt sehr ähnlich. Falls du trotzdem Probleme beim Lösen der Aufgabe hast, siehe dir Tipp 2 an.|2=Beispiel|3=Beispiel verbergen}} | |||
{{Lösung versteckt|1= | |||
* Bei '''drei Summanden''' wendest du die '''1. binomische Formel''' an. | |||
* Bei '''zwei Summanden und einem Minuenden''' wendest du die '''2. binomische Formel''' an. | |||
* Bei '''einem Summanden und einem Minuenden''' wendest du die '''3. binomische Formel''' an.|2=Tipp 2|3=Tipp ausblenden}}| 3=Arbeitsmethode}} | |||
{{Box | 1=Aufgabe 3: Warum ist das so?| 2= | {{Box | 1=Aufgabe 3: Warum ist das so?| 2= | ||
Aktuelle Version vom 16. Dezember 2020, 12:05 Uhr
1) Terme zusammenfassen
Einführung
Aufgaben
2) Terme ausmultiplizieren und faktorisieren
Terme ausmultiplizieren
Aufgabe
Terme faktorisieren
Aufgabe
Weitere Aufgaben zum Ausmultiplizieren und Faktorisieren
3) Binomische Formeln
Was sind die binomischen Formeln?
Herleitung der binomischen Formeln
Beispiele
Aufgaben