Digitale Werkzeuge in der Schule/Fit für VERA-8/Stochastik: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (64 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
In diesem Lernpfadkapitel kannst du deine Kenntnisse in der Stochastik verbessern und vertiefen. Es gibt drei Themengebiete, auf die du über das Inhaltsverzeichnis zugreifen kannst. | In diesem Lernpfadkapitel kannst du deine Kenntnisse in der Stochastik verbessern und vertiefen. Es gibt drei Themengebiete, auf die du über das Inhaltsverzeichnis zugreifen kannst. | ||
Zum Lösen der Aufgaben benötigst du Stift, Papier und deinen Taschenrechner. Bitte runde Dezimalzahlen auf | Zum Lösen der Aufgaben benötigst du Stift, Papier und deinen Taschenrechner. Bitte runde Dezimalzahlen auf zwei Nachkommastellen genau. | ||
Bei den Aufgaben unterscheiden wir folgende Typen: | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
| Zeile 22: | Zeile 22: | ||
| 2= | | 2= | ||
Die '''absolute Häufigkeit''' misst, wie oft ein bestimmtes Ereignis | Die '''absolute Häufigkeit''' misst, wie oft ein bestimmtes Ereignis bei mehrmaliger Wiederholung eines Zufallsexperiments auftritt. Als Anzahl ist sie immer eine natürliche Zahl zwischen <math>0</math> und der Gesamtzahl von Versuchen. | ||
| 3= Merksatz | | 3= Merksatz | ||
| Zeile 31: | Zeile 31: | ||
| 2= | | 2= | ||
Wenn ein Würfel <math>100</math> mal geworfen wird und <math>22</math> mal die Würfelzahl 6 herauskommt, beträgt die absolute Häufigkeit dafür <math>22</math>. | |||
| 3= Hervorhebung1}} | | 3= Hervorhebung1}} | ||
| Zeile 39: | Zeile 39: | ||
| 2= | | 2= | ||
Die '''relative Häufigkeit''' bezeichnet den Anteil der absoluten Häufigkeit (Anzahl) eines Ereignisses an der | Die '''relative Häufigkeit''' bezeichnet den Anteil der absoluten Häufigkeit (Anzahl) eines Ereignisses an der Gesamtzahl aller Ereignisse. Dieser Anteil wird entweder als Bruch dargestellt oder als Prozentwert angegeben. | ||
| 3= Merksatz | | 3= Merksatz | ||
| Zeile 48: | Zeile 48: | ||
| 2= | | 2= | ||
Bei 100 Würfen mit einem Würfel wird 22 mal die Würfelzahl 6 notiert. Die absolute Häufigkeit beträgt also 22 für die Würfelzahl 6. Um nun die relative Häufigkeit zu bestimmen, wird die absolute Häufigkeit durch die gesamte Anzahl an Würfelwürfen dividiert. | Bei <math>100</math> Würfen mit einem Würfel wird <math>22</math> mal die Würfelzahl 6 notiert. Die absolute Häufigkeit beträgt also <math>22</math> für die Würfelzahl 6. Um nun die relative Häufigkeit zu bestimmen, wird die absolute Häufigkeit durch die gesamte Anzahl an Würfelwürfen dividiert. | ||
In diesem Fall rechnet man: <math>\tfrac{22}{100}</math> | In diesem Fall rechnet man: <math>\tfrac{22}{100} = 0{,}22</math> | ||
Die relative Häufigkeit, dass eine 6 gewürfelt wurde, hat einen Anteil von <math>\tfrac{22}{100}</math> von der gesamten Würfelrunde und dadurch einen Prozentanteil von 22,00% = 0,22 \cdot 100,00%. | Die relative Häufigkeit, dass eine 6 gewürfelt wurde, hat einen Anteil von <math>\tfrac{22}{100}</math> von der gesamten Würfelrunde und dadurch einen Prozentanteil von <math>22{,}00</math> % <math>= 0{,}22 \cdot 100{,}00</math> %. | ||
| 3= Hervorhebung1}} | | 3= Hervorhebung1}} | ||
| Zeile 60: | Zeile 60: | ||
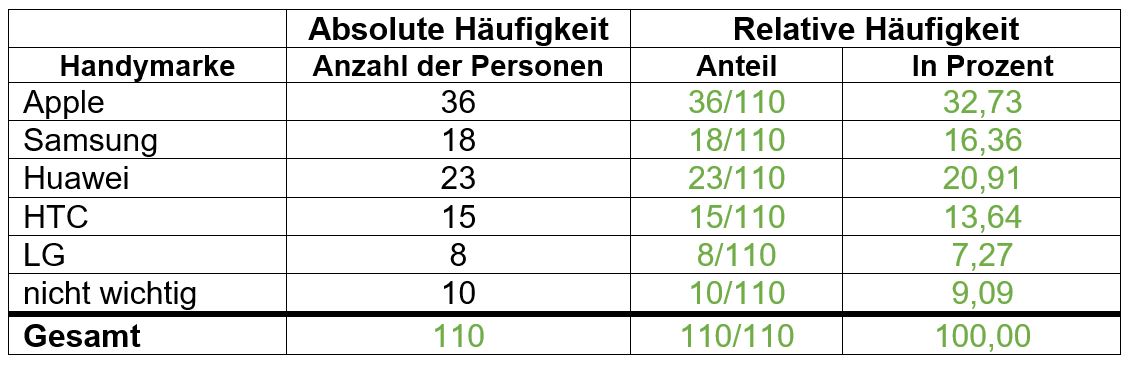
Auf dem Münsteraner Marktplatz wird eine Umfrage zum Thema Lieblingshandymarke durchgeführt. | Auf dem Münsteraner Marktplatz wird eine Umfrage zum Thema Lieblingshandymarke durchgeführt. | ||
36 Personen beantworteten die Frage mit „Apple“, | <math>10</math> Personen gaben bei der Umfrage an, dass ihnen die Handymarke nicht wichtig ist. <math>36</math> Personen beantworteten die Frage mit „Apple“, <math>8</math> Personen mit „LG“, <math>23</math> Personen mit „Huawei“, <math>15</math> Personen mit „HTC“ und <math>18</math> Personen mit „Samsung“. | ||
'''a)''' Fülle die Tabelle vollständig aus. Beachte, dass du den Bruch in folgender Form a/b eintippen | '''a)''' Fülle die Tabelle vollständig aus. Beachte, dass du den Bruch in folgender Form a/b eintippen solltest und ihn nicht kürzen darfst. | ||
{{(!}} class="wikitable" | {{(!}} class="wikitable" | ||
| Zeile 72: | Zeile 72: | ||
! Anzahl der Personen | ! Anzahl der Personen | ||
! Anteil | ! Anteil | ||
! Prozent | ! in Prozent | ||
{{!-}} | {{!-}} | ||
{{!}} Apple | {{!}} Apple | ||
{{!}} <div class="lueckentext-quiz"> '''36()''' </div> | {{!}} <div class="lueckentext-quiz"> '''36()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''36/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''36/110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''32,73 | {{!}} <div class="lueckentext-quiz"> '''32,73()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} Samsung | {{!}} Samsung | ||
{{!}} <div class="lueckentext-quiz"> '''18()''' </div> | {{!}} <div class="lueckentext-quiz"> '''18()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''18/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''18/110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''16,36 | {{!}} <div class="lueckentext-quiz"> '''16,36()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} Huawei | {{!}} Huawei | ||
{{!}} <div class="lueckentext-quiz"> '''23()''' </div> | {{!}} <div class="lueckentext-quiz"> '''23()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''23/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''23/110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''20,91 | {{!}} <div class="lueckentext-quiz"> '''20,91()''' </div> | ||
{{!-}} | |||
{{!}} HTC | |||
{{!}} <div class="lueckentext-quiz"> '''15()''' </div> | |||
{{!}} <div class="lueckentext-quiz"> '''15/110()''' </div> | |||
{{!}} <div class="lueckentext-quiz"> '''13,64()''' </div> | |||
{{!-}} | {{!-}} | ||
{{!}} LG | {{!}} LG | ||
{{!}} <div class="lueckentext-quiz"> '''8()''' </div> | {{!}} <div class="lueckentext-quiz"> '''8()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''8/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''8/110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''7,27 | {{!}} <div class="lueckentext-quiz"> '''7,27()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} nicht wichtig | {{!}} nicht wichtig | ||
{{!}} <div class="lueckentext-quiz"> '''10()''' </div> | {{!}} <div class="lueckentext-quiz"> '''10()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''10/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''10/110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''9,09 | {{!}} <div class="lueckentext-quiz"> '''9,09()''' </div> | ||
{{!-}} | {{!-}} | ||
! Gesamt | ! Gesamt | ||
{{!}} <div class="lueckentext-quiz"> '''110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''110/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''110/110()''' </div> | ||
{{!}} < | {{!}} <math>100{,}00</math> | ||
{{!)}} | {{!)}} | ||
{{Lösung versteckt| 1= Die richtigen Zahlen für die absolute Häufigkeit findest du im Aufgabentext. |2= | {{Lösung versteckt| 1= Die richtigen Zahlen für die absolute Häufigkeit findest du im Aufgabentext. |2= Absolute Häufigkeit |3= }} | ||
{{Lösung versteckt| 1= Die richtigen Anteilswerte erhältst du, wenn du die Anzahl der Personen und die Gesamtzahl in einem Bruch aufschreibst. |2= | {{Lösung versteckt| 1= Die richtigen Anteilswerte erhältst du, wenn du die Anzahl der Personen und die Gesamtzahl in einem Bruch aufschreibst. |2= Anteile |3= }} | ||
{{Lösung versteckt| 1= Für die Berechnung der Prozentzahlen nutzt du deinen Taschenrechner und dividierst die berechneten Anteile durch die Gesamtzahl. |2= | {{Lösung versteckt| 1= Für die Berechnung der Prozentzahlen nutzt du deinen Taschenrechner und dividierst die berechneten Anteile durch die Gesamtzahl. |2= Prozentzahl berechnen |3= }} | ||
{{Lösung versteckt| 1= | {{Lösung versteckt| 1= Runde die berechnete Prozentzahl auf zwei Nachkommastellen genau. |2= Prozentzahl runden |3= }} | ||
{{Lösung versteckt| 1=[[Datei: | {{Lösung versteckt| 1= [[Datei:Lösung-1a.jpg|zentriert]] |2= Lösung |3= }} | ||
'''b)''' Die | '''b)''' Die drei Bilder zeigen unterschiedliche Säulendiagramme. | ||
{{3Spalten | {{3Spalten | ||
| Zeile 135: | Zeile 135: | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{ Welches der | { Welches der drei Bilder zeigt das richtige Säulendiagramm für die absoluten Häufigkeitswerte zur Handyumfrage? } | ||
- Bild 1 | - Bild 1 | ||
+ Bild 2 | + Bild 2 | ||
| Zeile 147: | Zeile 147: | ||
{{Box | {{Box | ||
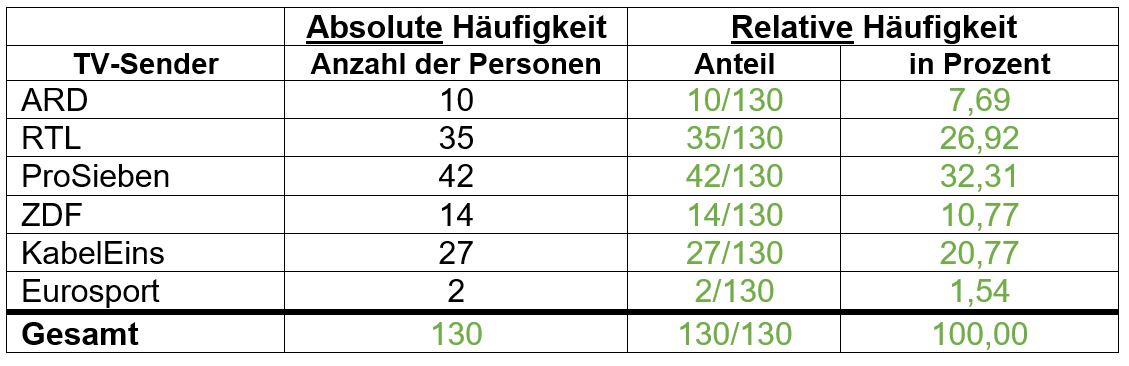
| 1= Aufgabe 2: | | 1= Aufgabe 2: TV Sender | ||
| 2= | | 2= | ||
Betrachte die durchgeführte Umfrage nach den beliebtesten TV-Sendern. | |||
Trage die Ergebnisse aus den einzelnen Teilaufgaben in das richtige Feld in der Tabelle ein. Für eine richtige Lösung der Anteile, solltest du den Bruch in folgender Form a/b eintippen und darfst ihn nicht kürzen. | |||
'''a)''' In welchen Tabellenfeldern fehlen die Begriffe „Relative“ und „Absolute"? | |||
<br /> | |||
'''b)''' Wie viele Personen wurden insgesamt befragt? | |||
<br /> | |||
'''c)''' Gib die Anteile und Prozentwerte der relativen Häufigkeit für jeden TV-Sender an. Runde dabei auf zwei Nachkommastellen. | |||
{{(!}} class="wikitable" | {{(!}} class="wikitable" | ||
| Zeile 202: | Zeile 168: | ||
! Anzahl der Personen | ! Anzahl der Personen | ||
! Anteil | ! Anteil | ||
! Prozent | ! in Prozent | ||
{{!-}} | {{!-}} | ||
{{!}} ARD | {{!}} ARD | ||
{{!}} 10 | {{!}} <math>10</math> | ||
{{!}} <div class="lueckentext-quiz"> '''10/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''10/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''7,69 | {{!}} <div class="lueckentext-quiz"> '''7,69()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} RTL | {{!}} RTL | ||
{{!}} 35 | {{!}} <math>35</math> | ||
{{!}} <div class="lueckentext-quiz"> '''35/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''35/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''26,92 | {{!}} <div class="lueckentext-quiz"> '''26,92()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} ProSieben | {{!}} ProSieben | ||
{{!}} 42 | {{!}} <math>42</math> | ||
{{!}} <div class="lueckentext-quiz"> '''42/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''42/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''32,31 | {{!}} <div class="lueckentext-quiz"> '''32,31()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} ZDF | {{!}} ZDF | ||
{{!}} 14 | {{!}} <math>14</math> | ||
{{!}} <div class="lueckentext-quiz"> '''14/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''14/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''10,77 | {{!}} <div class="lueckentext-quiz"> '''10,77()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} KabelEins | {{!}} KabelEins | ||
{{!}} 27 | {{!}} <math>27</math> | ||
{{!}} <div class="lueckentext-quiz"> '''27/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''27/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''20,77 | {{!}} <div class="lueckentext-quiz"> '''20,77()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} Eurosport | {{!}} Eurosport | ||
{{!}} 2 | {{!}} <math>2</math> | ||
{{!}} <div class="lueckentext-quiz"> '''2/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''2/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''1,54 | {{!}} <div class="lueckentext-quiz"> '''1,54()''' </div> | ||
{{!-}} | {{!-}} | ||
! Gesamt | ! Gesamt | ||
{{!}} <div class="lueckentext-quiz"> '''130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''130/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''130/130()''' </div> | ||
{{!}} < | {{!}} <math>100{,}00</math> | ||
{{!)}} | {{!)}} | ||
{{Lösung versteckt| 1= Die richtigen Anteilswerte erhältst du, wenn du die Anzahl der Personen und die Gesamtzahl in einem Bruch aufschreibst. |2= | {{Lösung versteckt| 1= Die richtigen Anteilswerte erhältst du, wenn du die Anzahl der Personen und die Gesamtzahl in einem Bruch aufschreibst. |2= Anteile |3= }} | ||
{{Lösung versteckt| 1= Für die Berechnung der Prozentzahlen nutzt du deinen Taschenrechner und dividierst die berechneten Anteile durch die Gesamtzahl. |2= | {{Lösung versteckt| 1= Für die Berechnung der Prozentzahlen nutzt du deinen Taschenrechner und dividierst die berechneten Anteile durch die Gesamtzahl. |2= Prozentzahl berechnen |3= }} | ||
{{Lösung versteckt| 1= | {{Lösung versteckt| 1= Runde die berechnete Prozentzahl auf zwei Nachkommastellen genau. |2= Prozentzahl runden |3= }} | ||
{{Lösung versteckt| 1= [[Datei: | {{Lösung versteckt| 1= [[Datei:Lösung-2.jpg|zentriert]]|2= Lösung |3= }} | ||
| 3= Arbeitsmethode | | 3= Arbeitsmethode | ||
| Zeile 261: | Zeile 221: | ||
{{Box | {{Box | ||
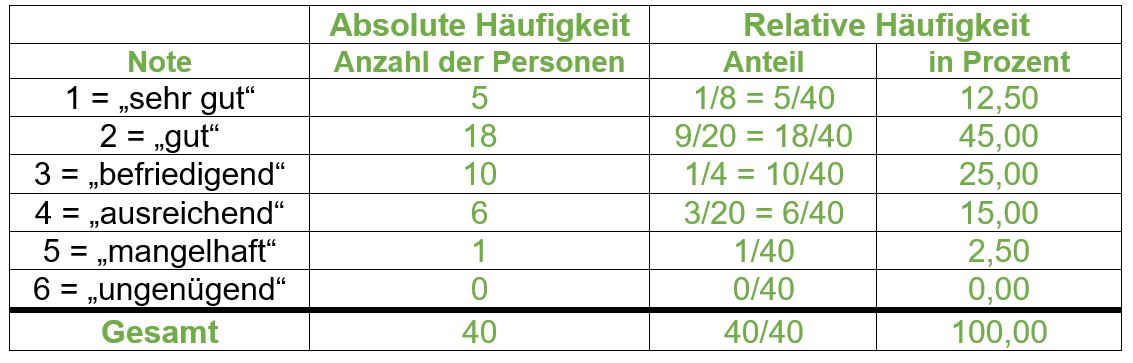
| 1= Aufgabe | | 1= Aufgabe 3: Hotelbewertung | ||
| 2= | | 2= | ||
Nach einem Hotelurlaub vergibt jede Person der 40-köpfigen Reisegruppe zur Bewertung eine Note für das Hotel. Es können die Noten 1 bis 6 vergeben werden. Die Note „sehr gut“ vergeben <math>\tfrac{1}{8}</math> der Reisegruppe. Die anderen Noten sind wie folgt verteilt: | Nach einem Hotelurlaub vergibt jede Person der <math>40</math>-köpfigen Reisegruppe zur Bewertung eine Note für das Hotel. Es können die Noten <math>1</math> bis <math>6</math> vergeben werden. Die Note „sehr gut“ vergeben <math>\tfrac{1}{8}</math> der Reisegruppe. Die anderen Noten sind wie folgt verteilt: | ||
<br /> | <br /> | ||
„gut“ <math>\tfrac{18}{40}</math> <br /> | „gut“ <math>\tfrac{18}{40}</math> <br /> | ||
| Zeile 282: | Zeile 242: | ||
! '''Note''' | ! '''Note''' | ||
! '''Anzahl der Personen''' | ! '''Anzahl der Personen''' | ||
! | ! Anteil | ||
! '''Prozent''' | ! '''in Prozent''' | ||
{{!-}} | {{!-}} | ||
{{!}} 1 = "sehr gut" | {{!}} <math>1</math> = "sehr gut" | ||
{{!}} | {{!}} | ||
{{!}} | {{!}} | ||
{{!}} | {{!}} | ||
{{!-}} | {{!-}} | ||
{{!}} 2 = "gut" | {{!}} <math>2</math> = "gut" | ||
{{!}} | {{!}} | ||
{{!}} | {{!}} | ||
{{!}} | {{!}} | ||
{{!-}} | {{!-}} | ||
{{!}} 3 = "befriedigend" | {{!}} <math>3</math> = "befriedigend" | ||
{{!}} | {{!}} | ||
{{!}} | {{!}} | ||
{{!}} | {{!}} | ||
{{!-}} | {{!-}} | ||
{{!}} 4 = "ausreichend" | {{!}} <math>4</math> = "ausreichend" | ||
{{!}} | {{!}} | ||
{{!}} | {{!}} | ||
{{!}} | {{!}} | ||
{{!-}} | {{!-}} | ||
{{!}} 5 = "mangelhaft" | {{!}} <math>5</math> = "mangelhaft" | ||
{{!}} | {{!}} | ||
{{!}} | {{!}} | ||
{{!}} | {{!}} | ||
{{!-}} | {{!-}} | ||
{{!}} 6 = "ungenügend" | {{!}} <math>6</math> = "ungenügend" | ||
{{!}} | {{!}} | ||
{{!}} | {{!}} | ||
| Zeile 322: | Zeile 282: | ||
</div> | </div> | ||
{{Lösung versteckt| 1= [[Datei:Lösung | {{Lösung versteckt| 1=[[Datei:Lösung-3a.jpg|zentriert]] |2= Lösung |3= }} | ||
<br /> | <br /> | ||
| Zeile 328: | Zeile 288: | ||
<br /> | <br /> | ||
'''b)''' Trage die in der Aufgabe genannten Anteile je Note in die Tabelle ein. Erweitere die Brüche dabei auf den Nenner 40. Berechne anschließend die Anzahl der Personen je Note und die dazu passende Prozentzahl. Trage auch diese Werte in die Tabelle ein. | '''b)''' Trage die in der Aufgabe genannten Anteile je Note in die Tabelle ein. Erweitere die Brüche dabei auf den Nenner <math>40</math>. Berechne anschließend die Anzahl der Personen je Note und die dazu passende Prozentzahl. Trage auch diese Werte in die Tabelle ein. | ||
{{(!}} class="wikitable" | {{(!}} class="wikitable" | ||
| Zeile 338: | Zeile 298: | ||
! Anzahl der Personen | ! Anzahl der Personen | ||
! Anteil | ! Anteil | ||
! Prozent | ! in Prozent | ||
{{!-}} | {{!-}} | ||
{{!}} 1 = "sehr gut" | {{!}} <math>1</math> = "sehr gut" | ||
{{!}} <div class="lueckentext-quiz"> '''5()''' </div> | {{!}} <div class="lueckentext-quiz"> '''5()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''5/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''5/40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''12,50 | {{!}} <div class="lueckentext-quiz"> '''12,50()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} 2 = "gut" | {{!}} <math>2</math> = "gut" | ||
{{!}} <div class="lueckentext-quiz"> '''18()''' </div> | {{!}} <div class="lueckentext-quiz"> '''18()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''18/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''18/40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''45,00 | {{!}} <div class="lueckentext-quiz"> '''45,00()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} 3 = "befriedigend" | {{!}} <math>3</math> = "befriedigend" | ||
{{!}} <div class="lueckentext-quiz"> '''10()''' </div> | {{!}} <div class="lueckentext-quiz"> '''10()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''10/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''10/40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''25,00 | {{!}} <div class="lueckentext-quiz"> '''25,00()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} 4 = "ausreichend" | {{!}} <math>4</math> = "ausreichend" | ||
{{!}} <div class="lueckentext-quiz"> '''6()''' </div> | {{!}} <div class="lueckentext-quiz"> '''6()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''6/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''6/40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''15, | {{!}} <div class="lueckentext-quiz"> '''15,00()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} 5 = "mangelhaft" | {{!}} <math>5</math> = "mangelhaft" | ||
{{!}} <div class="lueckentext-quiz"> '''1()''' </div> | {{!}} <div class="lueckentext-quiz"> '''1()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''1/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''1/40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''2,50 | {{!}} <div class="lueckentext-quiz"> '''2,50()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} 6 = "ungenügend" | {{!}} <math>6</math> = "ungenügend" | ||
{{!}} <div class="lueckentext-quiz"> '''0()''' </div> | {{!}} <div class="lueckentext-quiz"> '''0()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''0/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''0/40()''' </div> | ||
{{!}} < | {{!}} <math>0{,}00</math> | ||
{{!-}} | {{!-}} | ||
! Gesamt | ! Gesamt | ||
{{!}} <div class="lueckentext-quiz"> '''40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''40/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''40/40()''' </div> | ||
{{!}} < | {{!}} <math>100{,}00</math> | ||
{{!)}} | {{!)}} | ||
{{Lösung versteckt| 1= Für die Berechnung der Prozentzahlen nutzt du deinen Taschenrechner und dividierst die berechneten Anteile durch die Gesamtzahl. |2= Prozentzahl berechnen |3= }} | |||
{{Lösung versteckt| 1= [[Datei:Lösung- | {{Lösung versteckt| 1= Runde die berechnete Prozentzahl auf zwei Nachkommastellen genau. |2= Prozentzahl runden |3= }} | ||
{{Lösung versteckt| 1= [[Datei:Lösung-3b.jpg|zentriert]] |2= Lösung |3= }} | |||
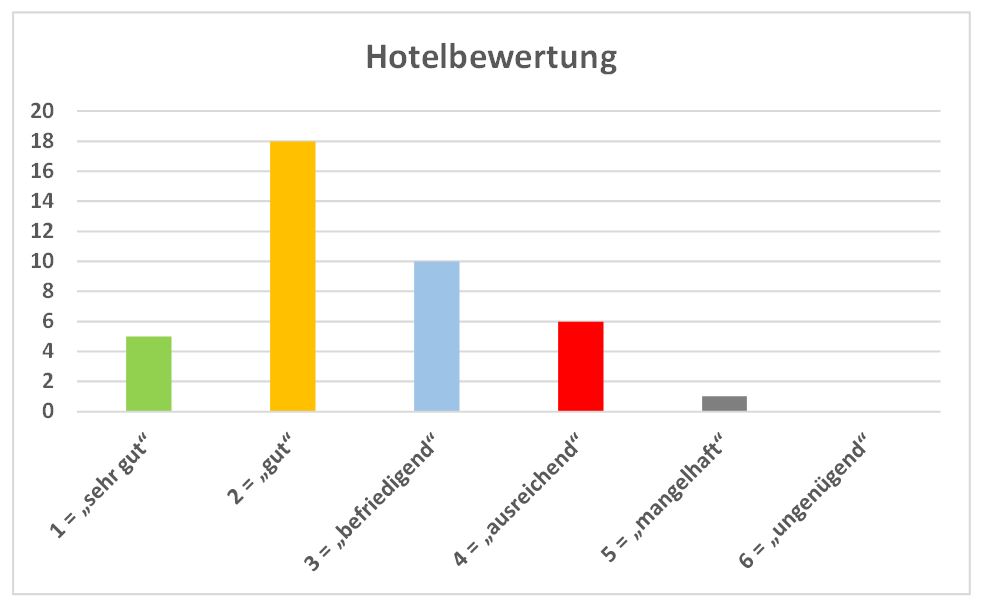
'''c)''' Zeichne ein Säulendiagramm, welches die absoluten Werte der Umfrage darstellt. | '''c)''' Zeichne ein Säulendiagramm, welches die absoluten Werte der Umfrage darstellt. | ||
{{Lösung versteckt| 1= [[Datei:Diagramm4-1.jpg | {{Lösung versteckt| 1= [[Datei:Diagramm4-1.jpg|zentriert]] |2= Lösung |3= }} | ||
| 3= Arbeitsmethode | | 3= Arbeitsmethode | ||
| Farbe={{Farbe|grün|dunkel}} | }} | ||
{{Box | |||
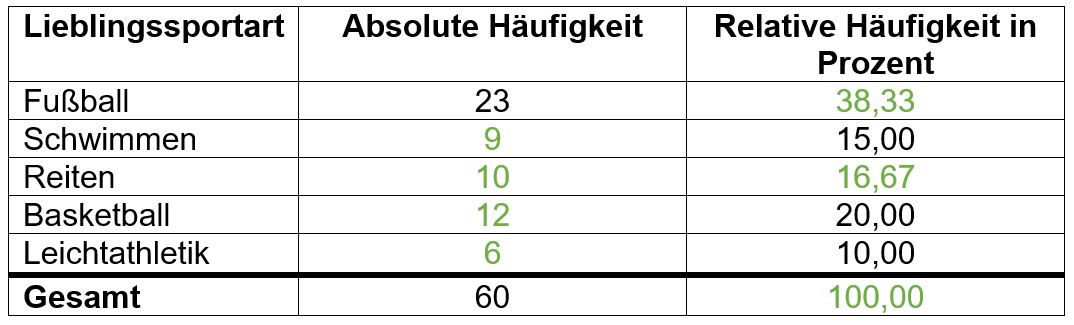
| 1= Aufgabe 4: Lieblingssportart | |||
| 2= Vervollständige die Tabelle: | |||
{{(!}} class="wikitable" | |||
! Lieblingssportart | |||
! Absolute Häufigkeit | |||
! Relative Häufigkeit in Prozent | |||
{{!-}} | |||
{{!}} Fußball | |||
{{!}} <math>23</math> | |||
{{!}} <div class="lueckentext-quiz"> '''38,33()''' </div> | |||
{{!-}} | |||
{{!}} Schwimmen | |||
{{!}} <div class="lueckentext-quiz"> '''9()''' </div> | |||
{{!}} <math>15{,}00</math> | |||
{{!-}} | |||
{{!}} Reiten | |||
{{!}} <div class="lueckentext-quiz"> '''10()''' </div> | |||
{{!}} <div class="lueckentext-quiz"> '''16,67()''' </div> | |||
{{!-}} | |||
{{!}} Basketball | |||
{{!}} <div class="lueckentext-quiz"> '''12()''' </div> | |||
{{!}} <math>20{,}00</math> | |||
{{!-}} | |||
{{!}} Leichtathletik | |||
{{!}} <div class="lueckentext-quiz"> '''6()''' </div> | |||
{{!}} <math>10{,}00</math> | |||
{{!-}} | |||
! Gesamt | |||
{{!}} <math>60</math> | |||
{{!}} <div class="lueckentext-quiz"> '''100,00()''' </div> | |||
{{!)}} | |||
{{Lösung versteckt| 1= Runde die berechnete Prozentzahl auf zwei Nachkommastellen genau. |2= Prozentzahl runden |3= }} | |||
{{Lösung versteckt| 1= [[Datei:Lösung-4.jpg|zentriert]] |2= Lösung |3= }} | |||
| 3= Arbeitsmethode | |||
| Farbe={{Farbe|grün|dunkel}} | |||
}} | }} | ||
| Zeile 391: | Zeile 396: | ||
| 2= | | 2= | ||
Julian und Max haben eine Verkehrszählung vor ihrer Haustür gemacht. Leider sind die Zettel mit den Strichlisten verloren gegangen. Max weiß aber noch, dass sie 8 Busse gezählt haben. | Julian und Max haben eine Verkehrszählung vor ihrer Haustür gemacht. Leider sind die Zettel mit den Strichlisten verloren gegangen. Max weiß aber noch, dass sie <math>8</math> Busse gezählt haben. | ||
{{(!}} class="wikitable" | {{(!}} class="wikitable" | ||
| Zeile 400: | Zeile 405: | ||
! Fahrrad | ! Fahrrad | ||
{{!-}} | {{!-}} | ||
{{!}} 45% | {{!}} <math>45{,}00</math> % | ||
{{!}} 15% | {{!}} <math>15{,}00</math> % | ||
{{!}} 10% | {{!}} <math>10{,}00</math> % | ||
{{!}} 5% | {{!}} <math>5{,}00</math> % | ||
{{!}} 25% | {{!}} <math>25{,}00</math> % | ||
{{!-}} | {{!-}} | ||
{{!}} <div class="lueckentext-quiz">'''36()'''</div> | {{!}} <div class="lueckentext-quiz">'''36()'''</div> | ||
| Zeile 414: | Zeile 419: | ||
<br /> | <br /> | ||
Wie viele Fahrzeuge haben Max und Julian insgesamt gezählt? | |||
Berechne hierzu die fehlenden Fahrzeuganzahlen und trage sie in die richtigen Felder der Tabelle ein. | |||
<div class="lueckentext-quiz">Max und Julian haben insgesamt '''80()''' Fahrzeuge gezählt.</div> | |||
{{Lösung versteckt| 1= Aus dem Aufgabentext weißt du, dass <math>8</math> Busse <math>10</math> % aller Fahrzeuge (F) sind. Für die anderen Fahrzeuganzahlen nutzt du den Dreisatz: | |||
<math>10</math> % <math>= 8</math> F | |||
<math> 1</math> % <math>= 8</math> F <math> : 10</math> % | |||
<math> x</math> % <math>= 8</math> F <math> : 10</math> % <math>\cdot x</math> % | |||
|2= Tipp Fahrzeuganzahl |3= }} | |||
{{Lösung versteckt| 1= Für die Gesamtzahl alles gezählten Fahrzeuge addierst du die einzelnen berechneten Fahrzeuganzahlen zusammen. | |||
|2= Tipp Gesamtzahl Fahrzeuge |3= }} | |||
{{Lösung versteckt| 1= Max und Julian haben insgesamt 80 Fahrzeuge gezählt. |2= Lösung |3= }} | {{Lösung versteckt| 1= [[Datei:Tabelle-5a.jpg|zentriert]] Max und Julian haben insgesamt <math>80</math> Fahrzeuge gezählt. |2= Lösung |3= }} | ||
| 3= Arbeitsmethode | | 3= Arbeitsmethode | ||
| Farbe={{Farbe|grün|dunkel}} | | Farbe={{Farbe|grün|dunkel}} | ||
}} | }} | ||
==Zufallsexperimente== | ==Zufallsexperimente== | ||
| Zeile 436: | Zeile 449: | ||
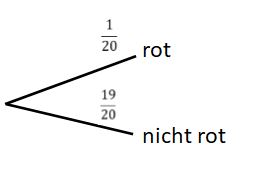
Die Wahrscheinlichkeit berechnet sich dann aus <math>\tfrac{\text{Anzahl der Ergebnisse zu gefragten Ereignis}}{\text{Anzahl aller möglichen Ergebnisse}} </math>. | Die Wahrscheinlichkeit berechnet sich dann aus <math>\tfrac{\text{Anzahl der Ergebnisse zu gefragten Ereignis}}{\text{Anzahl aller möglichen Ergebnisse}} </math>. | ||
Anders als bei der relativen Häufigkeit, | Anders als bei der relativen Häufigkeit, geht es hier nicht um die Erfassung von Daten, sondern um die Berechnung von Wahrscheinlichkeiten. | Merksatz}} | ||
{{Box | Baumdiagramme| | {{Box | Baumdiagramme| | ||
| Zeile 450: | Zeile 459: | ||
{{Box | Aufgabe 6: Klassendienste | | {{Box | Aufgabe 6: Klassendienste | | ||
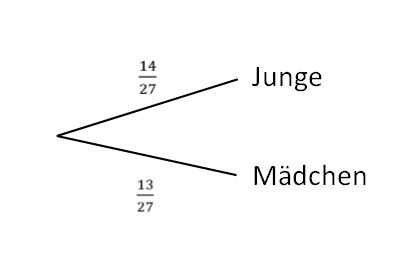
In einer Klasse sind 14 Jungen und 13 Mädchen. Es werden Beauftragte für verschiedene Klassendienste gelost. | In einer Klasse sind <math>14</math> Jungen und <math>13</math> Mädchen. Es werden Beauftragte für verschiedene Klassendienste gelost. | ||
'''a)''' Für den Blumendienst wird eine Person gelost. Wie groß ist die Wahrscheinlichkeit, dass es ein Junge ist? | '''a)''' Für den Blumendienst wird eine Person gelost. Wie groß ist die Wahrscheinlichkeit, dass es ein Junge ist? | ||
| Zeile 469: | Zeile 478: | ||
[[Datei:Baumdiagramm A1 a.jpg|zentriert]] | [[Datei:Baumdiagramm A1 a.jpg|zentriert]] | ||
Die Wahrscheinlichkeit, dass ein Junge den Dienst bekommt, liegt also bei <math>\tfrac{14}{27}</math> bzw. bei ungefähr <math>51{,}85 | Die Wahrscheinlichkeit, dass ein Junge den Dienst bekommt, liegt also bei <math>\tfrac{14}{27}</math> bzw. bei ungefähr <math>51{,}85</math> %. | ||
|2= Lösung |3= Lösung}} | |2= Lösung |3= Lösung}} | ||
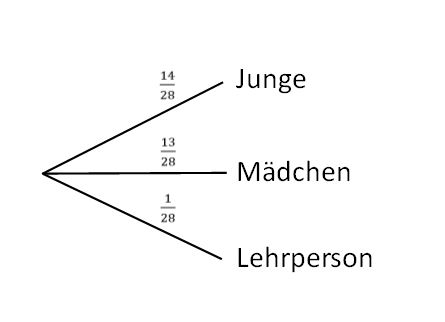
| Zeile 484: | Zeile 493: | ||
3. Die Lehrperson wird gelost. | 3. Die Lehrperson wird gelost. | ||
Auch hier ergeben sich die Wahrscheinlichen aus den relativen Häufigkeiten. Hierbei muss allerdings darauf geachtet werden, dass nicht nur die Anzahl der Schülerinnen und Schüler als gesamte Menge betrachtet wird, sondern auch die Lehrperson hinzu addiert wird. Es stehen also insgesamt 28 Personen zur Auswahl. Das Baumdiagramm sieht so aus: | Auch hier ergeben sich die Wahrscheinlichen aus den relativen Häufigkeiten. Hierbei muss allerdings darauf geachtet werden, dass nicht nur die Anzahl der Schülerinnen und Schüler als gesamte Menge betrachtet wird, sondern auch die Lehrperson hinzu addiert wird. Es stehen also insgesamt <math>28</math> Personen zur Auswahl. Das Baumdiagramm sieht so aus: | ||
[[Datei:Baumdiagramm A1 b.jpg|zentriert]] | [[Datei:Baumdiagramm A1 b.jpg|zentriert]] | ||
Die Wahrscheinlichkeit dafür, dass die Lehrperson selbst die Tafel putzen muss, liegt bei <math>\tfrac{1}{28}</math> bzw. bei <math>3{,}57 | Die Wahrscheinlichkeit dafür, dass die Lehrperson selbst die Tafel putzen muss, liegt bei <math>\tfrac{1}{28}</math> bzw. bei <math>3{,}57</math> %. | ||
|2= Lösung |3= Lösung}} | |2= Lösung |3= Lösung}} | ||
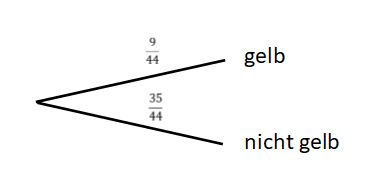
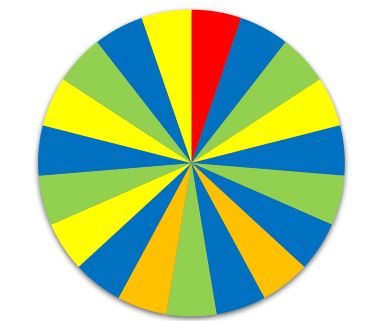
| Zeile 542: | Zeile 551: | ||
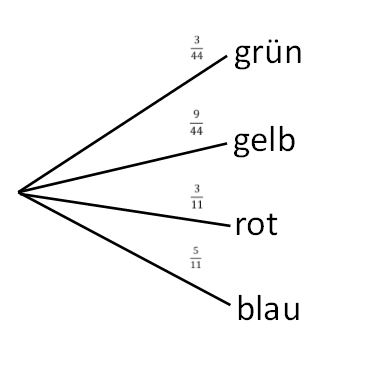
Rechne das nun in Prozent um: | Rechne das nun in Prozent um: | ||
<math>\tfrac{9}{44} \approx 0{,}2045 = 20{,}45 | <math>\tfrac{9}{44} \approx 0{,}2045 = 20{,}45</math> %. | ||
Die Wahrscheinlichkeit einen Stift zu gewinnen liegt bei <math>20{,}45 | Die Wahrscheinlichkeit einen Stift zu gewinnen liegt bei <math>20{,}45</math> %. | ||
|2= Lösung |3= Lösung }} | |2= Lösung |3= Lösung }} | ||
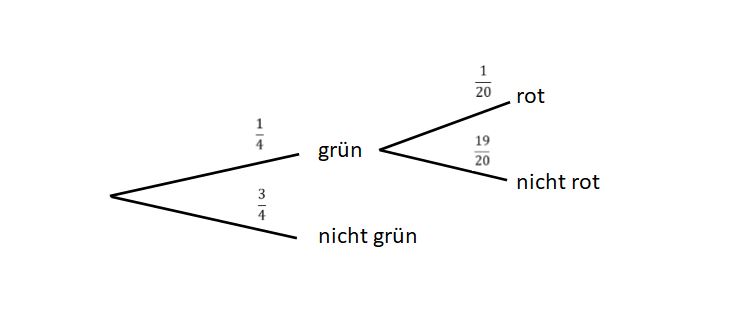
| Zeile 583: | Zeile 592: | ||
Nun rechnet man die Brüche in Prozent um: | Nun rechnet man die Brüche in Prozent um: | ||
Wahrscheinlichkeit zu verlieren: <math>\tfrac{5}{11} \approx 0{,}4545 = 45{,}45 | Wahrscheinlichkeit zu verlieren: <math>\tfrac{5}{11} \approx 0{,}4545 = 45{,}45</math> %. | ||
Wahrscheinlichkeit zu gewinnen: <math>100 %-45{,}45%=54{,}55 | Wahrscheinlichkeit zu gewinnen: <math>100</math> % <math>-45{,}45</math> % <math>=54{,}55</math> %. | ||
Die Wahrscheinlichkeit, zu gewinnen liegt bei <math>54{,}55 | Die Wahrscheinlichkeit, zu gewinnen liegt bei <math>54{,}55</math> %, die zu verlieren bei <math>45{,}45</math> %. Die Aussage stimmt also. | ||
|2= Lösung |3= Lösung }} | |2= Lösung |3= Lösung }} | ||
| Arbeitsmethode }} | | Arbeitsmethode }} | ||
{{Box | Pfadadditionsregel | | |||
Gehören zu einem Ereignis mehrere Pfade in einem Baumdiagramm, dann erhält man die Wahrscheinlichkeit des Ereignisses, indem man die Pfadwahrscheinlichkeiten der einzelnen zu dem Ereignis gehörenden Ergebnisse addiert. | |||
| Merksatz}} | |||
{{Box |Pfadmultiplikationsregel| | {{Box |Pfadmultiplikationsregel| | ||
| Zeile 601: | Zeile 613: | ||
<math>P(\text{Ereignis A} | \text{Ereignis B})= \text{Wahrscheinlichkeit A} \cdot \text{Wahrscheinlichkeit B} </math> | <math>P(\text{Ereignis A} | \text{Ereignis B})= \text{Wahrscheinlichkeit A} \cdot \text{Wahrscheinlichkeit B} </math> | ||
<math>*</math> Diese Schreibweise bedeutet, dass erst Ereignis A und danach Ereignis B eintritt. | |||
* Diese Schreibweise | |||
| Merksatz}} | | Merksatz}} | ||
| Zeile 658: | Zeile 669: | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||
==Laplace-Experimente== | ==Laplace-Experimente== | ||
| Zeile 666: | Zeile 676: | ||
Bei <math>n</math> Ergebnissen ist die Wahrscheinlichkeit in einem Laplace-Experiment für jedes Ergebnis <math>\tfrac{1}{n}</math>. | Bei <math>n</math> Ergebnissen ist die Wahrscheinlichkeit in einem Laplace-Experiment für jedes Ergebnis <math>\tfrac{1}{n}</math>. | ||
| Merksatz}} | | Merksatz}} | ||
{{Box | Aufgabe 9: Kartenspiel | | {{Box | Aufgabe 9: Kartenspiel | | ||
Bei einem Skatkartenspiel gibt es 12 Bildkarten. Es gibt 4 Buben, 4 Damen und 4 Könige. Karo und Herz werden auch „rote Karten“ genannt und Pik und Kreuz auch „schwarze Karten“. Berechne nun die Wahrscheinlichkeit, mit der du die angegebene Karte aus den 32 Spielkarten ziehst. | Bei einem Skatkartenspiel gibt es <math>12</math> Bildkarten. Es gibt <math>4</math> Buben, <math>4</math> Damen und <math>4</math> Könige. Karo und Herz werden auch „rote Karten“ genannt und Pik und Kreuz auch „schwarze Karten“. Berechne nun die Wahrscheinlichkeit, mit der du die angegebene Karte aus den <math>32</math> Spielkarten ziehst. | ||
[[Datei:Skat-Kartenspiel.jpg|mini]] | [[Datei:Skat-Kartenspiel.jpg|mini]] | ||
| Zeile 693: | Zeile 698: | ||
{{Lösung versteckt|1='''a)''' Die Gesamtmenge der Karten beträgt <math>32</math>. Die Wahrscheinlichkeit für jede einzelne Karte beträgt also <math>\tfrac{1}{32}</math> (Laplace). | {{Lösung versteckt|1='''a)''' Die Gesamtmenge der Karten beträgt <math>32</math>. Die Wahrscheinlichkeit für jede einzelne Karte beträgt also <math>\tfrac{1}{32}</math> (Laplace). | ||
Für das Ereignis eine Dame zu ziehen gibt es insgesamt 4 Karten. Also 4 mögliche Ergebnisse, dessen Wahrscheinlichkeiten nach der Summenregel addiert werden können. | Für das Ereignis eine Dame zu ziehen gibt es insgesamt <math>4</math> Karten. Also <math>4</math> mögliche Ergebnisse, dessen Wahrscheinlichkeiten nach der Summenregel addiert werden können. | ||
<math> P(\text{Dame wird gezogen}) = \tfrac{1}{32} + \tfrac{1}{32} + \tfrac{1}{32} + \tfrac{1}{32} = 4 \cdot \tfrac{1}{32} = \tfrac{4}{32} = \tfrac{1}{8} </math> | |||
Die Wahrscheinlichkeit eine Dame zu ziehen beträgt somit <math>\tfrac{1}{8}</math>. |2=Lösung a)|3=Lösung}} | |||
{{Lösung versteckt|1='''b)''' Es gibt insgesamt <math>8</math> Kreuz-Karten. | |||
{{ | Also gilt mit der Summenregel: | ||
<math>P(\text{Kreuz-Karte wird gezogen})=\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}=8\cdot\tfrac{1}{32}=\tfrac{8}{32}=\tfrac{1}{4}</math> | |||
Die Wahrscheinlichkeit eine Kreuz-Karte zu ziehen beträgt somit <math>\tfrac{1}{4}</math>.|2=Lösung b)|3=Lösung}} | |||
{{Lösung versteckt|1='''c)''' Es gibt 8 Pik und 8 Kreuz-Karten, also insgesamt 16 schwarze Karten. | {{Lösung versteckt|1='''c)''' Es gibt <math>8</math> Pik und <math>8</math> Kreuz-Karten, also insgesamt <math>16</math> schwarze Karten. | ||
Also gilt mit der Summenregel: P( | Also gilt mit der Summenregel: | ||
<math> P(\text{Schwarze Karte wird gezogen})=16\cdot\tfrac{1}{32}=\tfrac{16}{32}=\tfrac{1}{2} </math> | |||
Die Wahrscheinlichkeit eine schwarze Karte zu ziehen beträgt somit <math>\tfrac{1}{2}</math>.|2=Lösung c)|3=Lösung}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | Aufgabe 10: Scrabble| | {{Box | Aufgabe 10: Scrabble| | ||
| Zeile 717: | Zeile 729: | ||
'''a)''' Es wird ein D gezogen. | '''a)''' Es wird ein D gezogen. | ||
{{Lösung versteckt|1=Es gibt insgesamt 13 Spielsteine.|2=Allgemeiner Tipp |3=Tipp}} | {{Lösung versteckt|1=Es gibt insgesamt <math>13</math> Spielsteine.|2=Allgemeiner Tipp |3=Tipp}} | ||
| Zeile 731: | Zeile 743: | ||
{{Lösung versteckt|1='''a)''' Insgesamt gibt es 13 Spielsteine. Aufgrund der übereinstimmenden Größe und Beschaffenheit der Steine, ist die Wahrscheinlichkeit für jeden einzelnen Spielstein gleich und beträgt <math>\tfrac{1}{13}</math>. Aus diesem Grund handelt es sich bei dieser Aufgabe um ein Laplace Experiment. | {{Lösung versteckt|1='''a)''' Insgesamt gibt es <math>13</math> Spielsteine. Aufgrund der übereinstimmenden Größe und Beschaffenheit der Steine, ist die Wahrscheinlichkeit für jeden einzelnen Spielstein gleich und beträgt <math>\tfrac{1}{13}</math>. Aus diesem Grund handelt es sich bei dieser Aufgabe um ein Laplace Experiment. | ||
Da unter den Steinen nur einmal der Buchstabe D vorhanden ist gilt: | |||
<math>P(\text{D wird gezogen})=\tfrac{1}{13}</math>. | |||
Die Wahrscheinlichkeit den Buchstaben D zu ziehen beträgt somit <math>\tfrac{1}{13}</math>.|2=Lösung a)|3=Lösung}} | |||
{{Lösung versteckt|1='''b)''' | {{Lösung versteckt|1='''b)''' Es gibt zwei Spielsteine mit dem Buchstaben N, die jeweils mit einer Wahrscheinlichkeit von <math>\tfrac{1}{13}</math> gezogen werden. | ||
Wegen der Summenregel für Laplace-Experimente können die Wahrscheinlichkeiten der beiden möglichen Ergebnisse bzw. Spielsteine für das Ereignis addiert werden. | |||
Es gilt also: <math>P(\text{N wird gezogen})=\tfrac{1}{13}+\tfrac{1}{13}=\tfrac{2}{13}</math> | |||
Die Wahrscheinlichkeit den Buchstaben N zu ziehen beträgt somit <math>\tfrac{2}{13}</math>.|2=Lösung b)|3=Lösung}} | |||
{{Lösung versteckt|1='''c)''' | {{Lösung versteckt|1='''c)''' Es gibt insgesamt <math>3</math> Spielsteine mit dem Buchstaben O, die jeweils mit einer Wahrscheinlichkeit von <math>\tfrac{1}{13}</math> gezogen werden. Wegen der Summenregel für Laplace-Experimente können die Wahrscheinlichkeiten der drei möglichen Ergebnisse bzw. Spielsteine für das Ereignis addiert werden. | ||
Es | Es gilt also: <math>P(\text{O wird gezogen})=\tfrac{1}{13}+\tfrac{1}{13}+\tfrac{1}{13}= \tfrac{3}{13}</math> | ||
Die Wahrscheinlichkeit den Buchstaben O zu ziehen beträgt somit <math>\tfrac{3}{13}</math>.|2=Lösung c) |3=Lösung}} | |||
{{Lösung versteckt|1='''d)''' | {{Lösung versteckt|1='''d)''' Insgesamt gibt es einen Spielstein mit A und drei mit einem O. Die restlichen Vokale sind nicht vorhanden. | ||
Somit folgt mit der Summenregel: | |||
<math>P(\text{Vokal wird gezogen})=\tfrac{1}{13}+\tfrac{3}{13}=\tfrac{4}{13}</math> | |||
Die Wahrscheinlichkeit einen Vokal zu ziehen beträgt somit <math>\tfrac{4}{13}</math>.|2=Lösung d)|3=Lösung}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
| Zeile 762: | Zeile 776: | ||
Es wird mit zwei Würfeln gewürfelt. Wie hoch ist die Wahrscheinlichkeit, dass… | Es wird mit zwei Würfeln gewürfelt. Wie hoch ist die Wahrscheinlichkeit, dass… | ||
'''a)''' …ein Pasch gewürfelt wird? | '''a)''' …ein Pasch (Zweimal die gleiche Zahl, z.B. {1,1}) gewürfelt wird? | ||
'''b)''' …die Differenz der Augenzahlen gleich drei ist? | '''b)''' …die Differenz der Augenzahlen gleich drei ist? | ||
{{Lösung versteckt|1= Überlege dir, welche Zahlenkombinationen zu einer Differenz von 3 führen. Denke insbesondere daran, dass die einzelnen Kombinationen jeweils in zwei unterschiedlichen Reihenfolgen gewürfelt werden können.|2=Tipp |3=Tipp}} | {{Lösung versteckt|1= Überlege dir, welche Zahlenkombinationen zu einer Differenz von <math>3</math> führen. Denke insbesondere daran, dass die einzelnen Kombinationen jeweils in zwei unterschiedlichen Reihenfolgen gewürfelt werden können.|2=Tipp |3=Tipp}} | ||
'''c)''' …die Summe der Augenzahlen eine Primzahl ist? | '''c)''' …die Summe der Augenzahlen eine Primzahl ist? | ||
{{Lösung versteckt|1=Primzahl: ganze Zahl, die größer als 1 und nur durch 1 und sich selbst teilbar ist. | {{Lösung versteckt|1=Primzahl: ganze Zahl, die größer als <math>1</math> und nur durch <math>1</math> und sich selbst teilbar ist. | ||
{{Lösung versteckt|1=Die Primzahlen, die mit zwei Würfeln erreicht werden können, sind die 2, 3, 5, 7 | {{Lösung versteckt|1=Die Primzahlen, die mit zwei Würfeln erreicht werden können, sind die <math>2</math>, <math>3</math>, <math>5</math>, <math>7</math>, <math>11</math>. Überlege dir jetzt, mit welchen der möglichen Zahlenkombinationen von zwei Würfeln man mithilfe der Addition auf diese Primzahlen kommt.|2=Tipp 2 |3=Tipp}} | ||
|2=Tipp |3=Tipp}} | |2=Tipp |3=Tipp}} | ||
{{Lösung versteckt|1=Mit jeder Zahl kann ein Pasch geworfen werden. Es gibt demnach insgesamt | {{Lösung versteckt|1=Mit jeder Zahl kann ein Pasch geworfen werden. Es gibt demnach insgesamt sechs verschiedene Pasche. Da die jeweiligen Zahlen identisch sind, ist die Reihenfolge nicht zu betrachten. | ||
Das Ereignis ist also: E = | Das Ereignis ist also: <math>E=\lbrace\lbrace1,1\rbrace;\lbrace2,2\rbrace;\lbrace3,3\rbrace;\lbrace4,4\rbrace;\lbrace5,5\rbrace;\lbrace6,6\rbrace\rbrace</math> | ||
Es gibt somit insgesamt 6 verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt 36 verschiedene Zahlenkombinationen gibt. | Es gibt somit insgesamt <math>6</math> verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt <math>36</math> verschiedene Zahlenkombinationen gibt. | ||
Also folgt mit der Summenregel: P(E) = | Also folgt mit der Summenregel: | ||
<math>P(E)=\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}= 6 \cdot\tfrac{1}{36}=\tfrac{6}{36}=\tfrac{1}{6}</math>|2=Lösung a) |3=Lösung}} | |||
{{Lösung versteckt|1= Es gibt | {{Lösung versteckt|1= Es gibt <math>3</math> unterschiedliche Kombinationen von Zahlen, deren Differenz <math>3</math> beträgt. Die 4 und 1, die 5 und 2 & die 6 und 3. Die einzelnen Kombinationen können jeweils in zwei unterschiedlichen Reihenfolgen geworfen werden. | ||
Das Ereignis ist also: E = | Das Ereignis ist also: <math>E = \lbrace \lbrace1,4\rbrace; \lbrace4,1\rbrace; \lbrace2,5\rbrace; \lbrace5,2\rbrace; \lbrace3,6\rbrace; \lbrace6,3\rbrace \rbrace</math> | ||
Es gibt somit insgesamt 6 verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt 36 verschiedene Zahlenkombinationen gibt. | Es gibt somit insgesamt <math>6</math> verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt <math>36</math> verschiedene Zahlenkombinationen gibt. | ||
Also folgt mit der Summenregel: P(E) = | Also folgt mit der Summenregel: | ||
<math>P(E)=\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}=6\cdot\tfrac{1}{36}=\tfrac{6}{36}= \tfrac{1}{6}</math>|2=Lösung b) |3=Lösung}} | |||
{{Lösung versteckt|1=Die Primzahlen, die mit zwei Würfeln erreicht werden können, sind die 2, 3, 5, 7 | {{Lösung versteckt|1=Die Primzahlen, die mit zwei Würfeln erreicht werden können, sind die <math>2</math>, <math>3</math>, <math>5</math>, <math>7</math>, <math>11</math>. Es gibt <math>8</math> unterschiedliche Kombinationen von Zahlen, deren Summe eine dieser Primzahlen ist. Die 1+1, die 1+2, die 1+4, die 1+6, die 2+3, die 2+5, die 3+4 und die 5+6. Die einzelnen Kombinationen können jeweils in zwei unterschiedlichen Reihenfolgen geworfen werden, außer das 1er-Pasch. | ||
Das Ereignis ist also: E = | Das Ereignis ist also: <math>E = \lbrace \lbrace1,1\rbrace; \lbrace1,2\rbrace; \lbrace2,1\rbrace; \lbrace1,4\rbrace; \lbrace4,1\rbrace; \lbrace1,6\rbrace; \lbrace6,1\rbrace; \lbrace2,3\rbrace; \lbrace3,2\rbrace; \lbrace2,5\rbrace; \lbrace5,2\rbrace; \lbrace3,4\rbrace; \lbrace4,3\rbrace; \lbrace5,6\rbrace; \lbrace6,5\rbrace \rbrace</math> | ||
Es gibt somit insgesamt 15 verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt 36 verschiedene Zahlenkombinationen gibt. | Es gibt somit insgesamt <math>15</math> verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt <math>36</math> verschiedene Zahlenkombinationen gibt. | ||
Also folgt mit der Summenregel: P(E) = 15 | Also folgt mit der Summenregel: | ||
<math>P(E)=15\cdot\tfrac{1}{36}=\tfrac{15}{36}</math>|2=Lösung c) |3=Lösung}} | |||
| Arbeitsmethode }} | | Arbeitsmethode }} | ||
| Zeile 810: | Zeile 827: | ||
Julia sagt: „Deine Chance in dein Haus zu kommen ist beim nächsten Wurf viel größer als meine.“ | Julia sagt: „Deine Chance in dein Haus zu kommen ist beim nächsten Wurf viel größer als meine.“ | ||
'''a)''' Hat Julia recht mit ihrer Behauptung? | '''a)''' Hat Julia recht mit ihrer Behauptung? Begründe deine Antwort. | ||
{{Lösung versteckt|1=Überlege dir, welche Zahlen Markus und Julia würfeln können, um in das Haus zu kommen.|2=Tipp |3=Tipp}} | {{Lösung versteckt|1=Überlege dir, welche Zahlen Markus und Julia würfeln können, um in das Haus zu kommen.|2=Tipp |3=Tipp}} | ||
| Zeile 819: | Zeile 836: | ||
{{Lösung versteckt|1=Von Julia kann eine 1, 2, 3 oder 4 gewürfelt werden. | {{Lösung versteckt|1=Von Julia kann eine 1, 2, 3 oder 4 gewürfelt werden. | ||
{{Lösung versteckt|1=Betrachte die vier verschiedene Fälle einzeln. Mit welchen Zahlen könnte Julia dann im nächsten Zug in ihr Haus kommen? | {{Lösung versteckt|1=Betrachte die vier verschiedene Fälle einzeln. Mit welchen Zahlen könnte Julia dann im nächsten Zug in ihr Haus kommen? | ||
{{Lösung versteckt|1=Berechne nun die Wahrscheinlichkeit, dass Julia eine der Zahlen würfelt und vergleiche diese mit der Wahrscheinlichkeit von Markus ins Haus zu kommen.|2= | {{Lösung versteckt|1=Berechne nun die Wahrscheinlichkeit, dass Julia eine der Zahlen würfelt und vergleiche diese mit der Wahrscheinlichkeit von Markus ins Haus zu kommen.|2=Tipp 4 |3=Tipp}} | ||
|2= | |2=Tipp 3 |3=Tipp}} | ||
|2= | |2=Tipp 2 |3=Tipp}} | ||
|2=Tipp |3=Tipp}} | |2=Tipp |3=Tipp}} | ||
{{Lösung versteckt|1='''a)''' Markus benötigt eine 1, 2 oder 3, um in das Haus zu kommen. | {{Lösung versteckt|1='''a)''' Markus benötigt eine 1, 2 oder 3, um in das Haus zu kommen. | ||
Da der Würfel sechs Zahlen aufweist, beträgt die Wahrscheinlichkeit für jede einzelne Zahl <math>\tfrac{1}{6}</math> und somit gilt mit der Summenregel, da Markus drei der sechs Zahlen würfeln kann: | |||
<math>P(\text{Markus würfelt eine 1, 2 oder 3})=\tfrac{1}{6}+\tfrac{1}{6}+\tfrac{1}{6}=\tfrac{3}{6}=\tfrac{1}{2}</math> | |||
Julia kommt hingegen nur mit einer 5 oder 6 in ihr Haus. | Julia kommt hingegen nur mit einer 5 oder 6 in ihr Haus. | ||
Da Julia nur zwei der sechs Zahlen würfeln kann, gilt: | |||
<math>P(\text{Julia würfelt eine 5 oder 6})=\tfrac{1}{6}+\tfrac{1}{6}=\tfrac{2}{6}=\tfrac{1}{3}</math> | |||
Somit ist die Wahrscheinlichkeit, dass Markus mit dem nächsten Zug in sein Haus kommt größer als die von Julia. Aus diesem Grund hat Julia mit ihrer Behauptung recht. |2=Lösung a)|3=Lösung}} | |||
Somit ist die Wahrscheinlichkeit, dass Markus mit dem nächsten Zug in sein Haus kommt größer als die von Julia.|2=Lösung a)|3=Lösung}} | |||
{{Lösung versteckt|1='''b)''' Die Wahrscheinlichkeit von Markus in sein Haus zu kommen ist immer noch dieselbe wie zuvor, da er weiterhin direkt vor seinem Haus steht. | {{Lösung versteckt|1='''b)''' Die Wahrscheinlichkeit von Markus in sein Haus zu kommen ist immer noch dieselbe wie zuvor, da er weiterhin direkt vor seinem Haus steht. | ||
1. Fall: Julia | 1. Fall: Julia hat eine 1 gewürfelt | ||
Dann kann Julia mit den Zahlen 4, 5 und 6 beim darauffolgenden Zug ins Haus kommen. | Dann kann Julia mit den Zahlen 4, 5 und 6 beim darauffolgenden Zug ins Haus kommen. | ||
<math>P(\text{Julia würfelt eine 4, 5 oder 6})=\tfrac{1}{6}+\tfrac{1}{6}+\tfrac{1}{6}=3 \cdot\tfrac{1}{6}=\tfrac{3}{6}=\tfrac{1}{2}</math> | |||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
2. Fall: Julia | 2. Fall: Julia hat eine 2 gewürfelt | ||
Dann kann Julia mit den Zahlen 3, 4 und 5 beim darauffolgenden Zug ins Haus kommen: | Dann kann Julia mit den Zahlen 3, 4 und 5 beim darauffolgenden Zug ins Haus kommen: | ||
<math>P(\text{Julia würfelt eine 3, 4 oder 5})=3 \cdot\tfrac{1}{6}=\tfrac{1}{2}</math> | |||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
3. Fall: Julia | 3. Fall: Julia hat eine 3 gewürfelt | ||
Dann kann Julia mit den Zahlen 2, 3 und 4 beim darauffolgenden Zug ins Haus kommen: | Dann kann Julia mit den Zahlen 2, 3 und 4 beim darauffolgenden Zug ins Haus kommen: | ||
<math>P(\text{Julia würfelt eine 2, 3 oder 4})=3 \cdot\tfrac{1}{6}=\tfrac{1}{2}</math> | |||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
4. Fall: Julia | 4. Fall: Julia hat eine 4 gewürfelt | ||
Dann kann Julia mit den Zahlen 1, 2 und 3 beim darauffolgenden Zug ins Haus kommen: | Dann kann Julia mit den Zahlen 1, 2 und 3 beim darauffolgenden Zug ins Haus kommen: | ||
<math>P(\text{Julia würfelt eine 1, 2 oder 3})=3 \cdot\tfrac{1}{6}=\tfrac{1}{2}</math> | |||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
Wenn also beide einmal an der Reihe waren ohne ins Haus zu setzen, ist die Wahrscheinlichkeit dann für beide gleich beim nächsten Zug ins Haus zu kommen. Sie beträgt <math>\tfrac{1}{2}</math>. | Wenn also beide einmal an der Reihe waren ohne ins Haus zu setzen, ist die Wahrscheinlichkeit dann für beide gleich beim nächsten Zug ins Haus zu kommen. Sie beträgt <math>\tfrac{1}{2}</math>. | ||
|2=Lösung b)|3=Lösung}} | |2=Lösung b)|3=Lösung}} | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||
Aktuelle Version vom 14. Dezember 2020, 20:19 Uhr
Absolute und relative Häufigkeit
Zufallsexperimente
Laplace-Experimente