Buss-Haskert/Potenzen: Unterschied zwischen den Versionen
K (Tabelle und Einstiegsaufgabe ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (38 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
SEITE IM AUFBAU !!! | SEITE IM AUFBAU !!! | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
<br> | |||
{{Navigation| | |||
[[Buss-Haskert/Potenzen|1) Potenzen: Definition]]<br> | |||
[[Buss-Haskert/Potenzen/Potenzgesetze|2) Potenzgesetze]]<br> | |||
[[Buss-Haskert/Potenzen/Wissenschaftliche Schreibweise|3) Sehr große und sehr kleine Zahlen: Wissenschaftliche Schreibweise]]<br> | |||
[[Benutzer:Buss-Haskert/Wurzeln|4) Wurzeln: Definition]]<br> | |||
[[Benutzer:Buss-Haskert/Wurzeln/Rechnen mit Quadratwurzeln|5) Rechnen mit Quadratwurzeln]]}} | |||
<br> | |||
<ggb_applet id="haq8utkf" width="1170" height="790" border="888888" />(Applet von Matthias Hornof) | |||
<br> | |||
{{Box|Lernpfad Potenzen: Sehr große und sehr kleine Zahlen|[[Datei:Solar-system-11111 1280.jpg|rahmenlos|320px]] [[Datei:Virus-1812092 1920.jpg|rahmenlos|400px]]<br> | {{Box|Lernpfad Potenzen: Sehr große und sehr kleine Zahlen|[[Datei:Solar-system-11111 1280.jpg|rahmenlos|320px]] [[Datei:Virus-1812092 1920.jpg|rahmenlos|400px]]<br> | ||
In diesem Lernpfad lernst du | In diesem Lernpfad lernst du | ||
* wie man mit Potenzen rechnet (Potenzgesetzte) | * wie man mit Potenzen rechnet (Potenzgesetzte), | ||
* wie man sehr große und sehr kleine Zahlen mit Potenzen schreibt<br> | * wie man sehr große und sehr kleine Zahlen mit Potenzen schreibt,<br> | ||
* was Wurzeln sind und wie man mit ihnen rechnet und | |||
* wie du Wurzelterme umformen und vereinfachen kannst. | |||
Bearbeite die Schritte des Lernpfades selbständig. Stelle Fragen, wo du unsicher bist. Achte auf die Zeit!!<br><br> | Bearbeite die Schritte des Lernpfades selbständig. Stelle Fragen, wo du unsicher bist. Achte auf die Zeit!!<br><br> | ||
| Zeile 9: | Zeile 23: | ||
=== | ===Vorwissen=== | ||
| Zeile 53: | Zeile 67: | ||
| - Potenzen als Produkt schreiben und berechnen. | | - Potenzen als Produkt schreiben und berechnen. | ||
| Nr. 3 | |Nr. 3 | ||
|{{LearningApp|app=phmmugwen19|width=100%|height=200px}} | |{{LearningApp|app=phmmugwen19|width=100%|height=200px}} | ||
| Zeile 69: | Zeile 83: | ||
<br /> | <br /> | ||
==1) Potenzen== | |||
===Definition Potenzen=== | |||
[[Datei:Schachbrett.jpg|links|rahmenlos]]Einer Legende nach hat der indische Erfinder des Schachspiels dieses seinem Herrscher zum Geschenk gemacht. Also Belohnung wünschte er sich für das erste Feld 1 Reiskorn und für jedes weitere doppelt so viele Körner wie auf dem vorherigen.<br> | |||
a) Wie viele Reiskörner liegen/lägen auf dem letzten Feld?<br> | |||
b) Wie viele Reiskörner hat er insgesamt bekommen?<br> | |||
c) Ein Reiskorn wiegt ca. 65mg. Wie schwer wären alle Reiskörner zusammen?<br> | |||
d) Vergleiche das Gewicht mit der Weltjahresernte an Reis des letzten Jahres. (Recherchiere).<br> | |||
Übertrage die nachfolgende Tabelle in dein Heft und fülle sie aus:<br> | Übertrage die nachfolgende Tabelle in dein Heft und fülle sie aus:<br> | ||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 89: | Zeile 108: | ||
|20 | |20 | ||
|... | |... | ||
|- | |||
! style="width:10%;" |Anzahl der Reiskörner auf dem Feld | ! style="width:10%;" |Anzahl der Reiskörner auf dem Feld | ||
|1 | |1 | ||
| Zeile 104: | Zeile 123: | ||
| | | | ||
| | | | ||
|- | |||
!Anzahl in (Zweier-)Potenzen | !Anzahl in (Zweier-)Potenzen | ||
|2<sup>0</sup> | |2<sup>0</sup> | ||
| Zeile 121: | Zeile 140: | ||
|- | |- | ||
|} | |} | ||
Die Anzahl der Reiskörner pro Feld verdoppelt sich immer, wir rechnen: | |||
1. Feld: 1<br> | |||
2. Feld: 2<br> | |||
3. Feld: 2∙2 = 4<br> | |||
4. Feld: 2∙2∙2 = 8<br> | |||
5. Feld: 2∙2∙2∙2 = 16<br> | |||
usw.<br> | |||
Die Produkte schreiben wir als Potenz:<br> | |||
1. Feld: 1<br> | |||
2. Feld: 2<br> | |||
3. Feld: 2∙2 = 2<sup>2</sup> = 4<br> | |||
4. Feld: 2∙2∙2 = 2<sup>3</sup> = 8<br> | |||
5. Feld: 2∙2∙2∙2 = 2<sup>4</sup> =16<br> | |||
<br> | |||
{{Lösung versteckt|1=Auf dem letzten Feld lägen 2<sup>63</sup><math>\approx</math>9 223 400 000 000 000 000 Reiskörner.|2=Lösung zu a)|3=Verbergen}} | |||
{{Lösung versteckt|1=Um die Anzahl der Reiskörner insgesamt zu berechnen, muss die Summe aller Körner berechnet werden (nutze eine Tabellenkalkalkulation):<br> | |||
2<sup>0</sup>+2<sup>1</sup>+2<sup>3</sup>+ ... +2<sup>63</sup><br> = 1,84467<math>\cdot</math>10<sup>19</sup><br><math>\approx</math>18 446 700 000 000 000 000 |2=Lösung zu b)|3=Verbergen}} | |||
{{Lösung versteckt|1=Die Anzahl der Reiskörner muss nun mit dem Gewicht multipliziert werden, also <br> | |||
18 446 700 000 000 000 000 <math>\cdot</math> 65mg = 1,19904<math>\cdot</math>10<sup>21</sup><br> | |||
<math>\approx</math>1 199 040 000 000 000 000 000 mg.<br> | |||
Wandle diese Angabe von mg um in t, also teile durch 1000 000 000.<br> | |||
Das Gewicht beträgt also ca. 199 040 000 000 t, kurz 199,04 Milliarden Tonnen, also ein Vielfaches der Weltjahresernte.|2=Lösung zu c)|3=Verbergen}} | |||
Ein Produkt aus gleichen Faktoren schreiben wir verkürzt als Potenz. Merke dir die nachfolgenden Begriffe! | |||
{{Box|1=Definition Potenz|2= Ein Produkt aus n gleichen Faktoren a kann man verkürzt als Potenz schreiben.<br> | |||
[[Datei:Definition Potenz.png|rahmenlos|150px]].<br> | |||
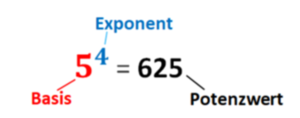
Beispiel:<br> | |||
5 · 5 · 5 · 5 = 5<sup>4</sup> = 625<br> | |||
[[Datei:Begriffe Potenz.png|rahmenlos|300px]]<br> | |||
Merke a<sup>0</sup> = 1; a<sup>1</sup> = a|3=Arbeitsmethode}} | |||
{{LearningApp|app=p0wn5y21c19|width=100%|height=600px}} | |||
===Potenzen berechnen=== | |||
{{Box|Übung 1 (*)|Löse die nachfolgenden Apps zum Kopfrechnen mit Potenzen | |||
|Üben}} | |||
{{LearningApp|app=ptmazgnba20|width=100%|height=600px}}<br><br> | |||
{{H5p-zum|id=8690|height=400px}}<br> | |||
{{Box|Übung 2 (**)|Löse die folgenden Aufgaben aus dem Buch. Achte auf eine vollständige und übersichtliche Darstellung. | |||
* S. 55 Nr. 7 | |||
* S. 55 Nr. 8 | |||
* S. 55 Nr. 9 | |||
* S. 55 Nr. 11|Üben}} | |||
{{Lösung versteckt|1=64 = 8<sup>2</sup> = 4<sup>3</sup> = 2<sup>6</sup>|2=Tipp zu Nr. 7|3=Verbergen}} | |||
{{Lösung versteckt|1=a) -2<sup>4</sup> = -2·2·2·2 = -16, denn das Minuszeichen wird nicht mit potenziert. <br> | |||
2<sup>4</sup> = 16<br> | |||
b) (-3)<sup>3</sup> = (-3)·(-3)·(-3) = -27, denn hier wird auch das Minuszeichen mit potenziert, da es mit in der Klammer steht. <br> | |||
-3<sup>Hochstellen</sup> = -3·3·3 = -27, hier wird das Minuszeichen nicht mit potenziert.|2= Tipp zu Nr. 8 (Minuszeichen)|3=Verbergen}} | |||
<br> | |||
{{Box|Übung 3 (***)|Löse die Anwendungsaufgabe. Achte auf eine vollständige und übersichtliche Darstellung. | |||
* S. 55 Nr. 15 | |||
* S. 55 Nr. 16|Üben}} | |||
{{Lösung versteckt|Nach einer halben Stunde sind also 700·2 Keime vorhanden, nach einer weiteren halben Stunde 700·2·2 usw.Die Verdopplung geschieht jede halbe Stunde. Wie oft können sich die Keime dann in sechs Stunden verdoppeln?|Tipp zu Nr. 15a|Verbergen}} | |||
{{Lösung versteckt|1= Löse durch Probieren: 700·2<sup>?</sup> = 1000000000 ? Nutze den Taschenrechner|2=Tipp zu Nr. 15b|3=Verbergen}}<br> | |||
<br> | |||
{{Fortsetzung|weiter=2) Potenzgesetze|weiterlink=Buss-Haskert/Potenzen/Potenzgesetze}} | |||
Aktuelle Version vom 15. Februar 2021, 08:05 Uhr
SEITE IM AUFBAU !!!
1) Potenzen: Definition
2) Potenzgesetze
3) Sehr große und sehr kleine Zahlen: Wissenschaftliche Schreibweise
4) Wurzeln: Definition

(Applet von Matthias Hornof)
Vorwissen
Bearbeite die Aufgaben in der Tabelle: (Buch: Schnittpunkt Mathematik - Differenzierende Ausgabe 9, Klett)
| Ich kann ... | Buch S. 52 | Übungen online |
|---|---|---|
| - Terme berechnen (Vorrangregeln) | Nr. 4 |
|
| - Zahlen runden. | Nr. 2 |
|
| - die Quadratzahlen auswendig. | Nr. 6 |
|
| - Potenzen als Produkt schreiben und berechnen. | Nr. 3 |
|
Vergleiche deine Lösungen mit den Lösungen hinten im Buch!
1) Potenzen
Definition Potenzen
Einer Legende nach hat der indische Erfinder des Schachspiels dieses seinem Herrscher zum Geschenk gemacht. Also Belohnung wünschte er sich für das erste Feld 1 Reiskorn und für jedes weitere doppelt so viele Körner wie auf dem vorherigen.
a) Wie viele Reiskörner liegen/lägen auf dem letzten Feld?
b) Wie viele Reiskörner hat er insgesamt bekommen?
c) Ein Reiskorn wiegt ca. 65mg. Wie schwer wären alle Reiskörner zusammen?
d) Vergleiche das Gewicht mit der Weltjahresernte an Reis des letzten Jahres. (Recherchiere).
Übertrage die nachfolgende Tabelle in dein Heft und fülle sie aus:
| Feld | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... | 20 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl der Reiskörner auf dem Feld | 1 | 2 | 4 | 8 | |||||||||
| Anzahl in (Zweier-)Potenzen | 20 | 21 | 22 | 23 |
Die Anzahl der Reiskörner pro Feld verdoppelt sich immer, wir rechnen:
1. Feld: 1
2. Feld: 2
3. Feld: 2∙2 = 4
4. Feld: 2∙2∙2 = 8
5. Feld: 2∙2∙2∙2 = 16
usw.
Die Produkte schreiben wir als Potenz:
1. Feld: 1
2. Feld: 2
3. Feld: 2∙2 = 22 = 4
4. Feld: 2∙2∙2 = 23 = 8
5. Feld: 2∙2∙2∙2 = 24 =16
Um die Anzahl der Reiskörner insgesamt zu berechnen, muss die Summe aller Körner berechnet werden (nutze eine Tabellenkalkalkulation):
= 1,844671019
18 446 700 000 000 000 000
Die Anzahl der Reiskörner muss nun mit dem Gewicht multipliziert werden, also
18 446 700 000 000 000 000 65mg = 1,199041021
1 199 040 000 000 000 000 000 mg.
Wandle diese Angabe von mg um in t, also teile durch 1000 000 000.
Ein Produkt aus gleichen Faktoren schreiben wir verkürzt als Potenz. Merke dir die nachfolgenden Begriffe!
Potenzen berechnen
a) -24 = -2·2·2·2 = -16, denn das Minuszeichen wird nicht mit potenziert.
24 = 16
b) (-3)3 = (-3)·(-3)·(-3) = -27, denn hier wird auch das Minuszeichen mit potenziert, da es mit in der Klammer steht.