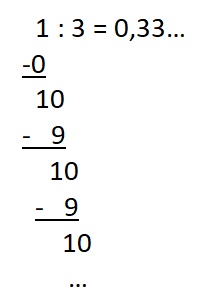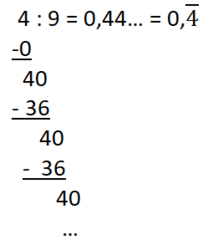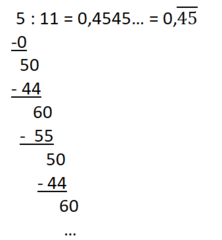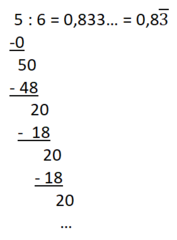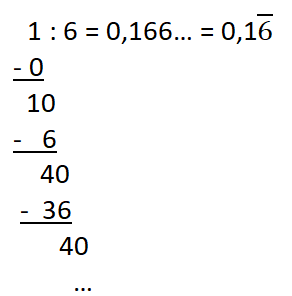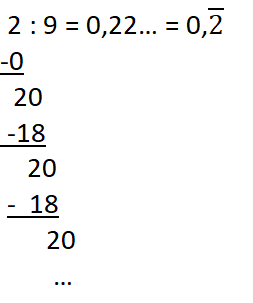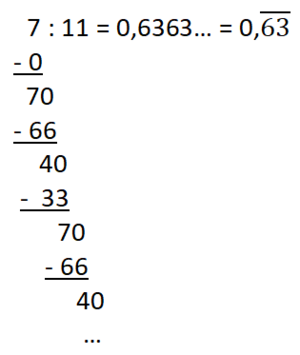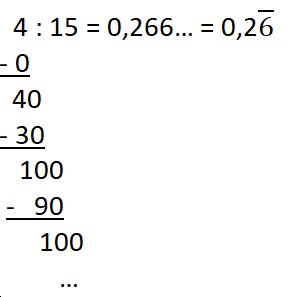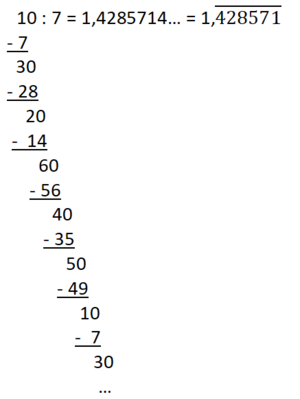Herta-Lebenstein-Realschule/Dezimalbrüche selbständig erarbeiten/4) Periodische Dezimalbrüche: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (Navigation ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation | [[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
<br> | |||
{{Navigation|[[Herta-Lebenstein-Realschule/Dezimalbrüche selbständig erarbeiten|Startseite - Vorwissen]] | |||
[[Herta-Lebenstein-Realschule/Dezimalbr%C3%BCche_selbst%C3%A4ndig_erarbeiten/1) Dezimalbr%C3%BCche_in_der_Stellenwerttafel|1) Dezimalbrüche in der Stellenwerttafel]] | [[Herta-Lebenstein-Realschule/Dezimalbr%C3%BCche_selbst%C3%A4ndig_erarbeiten/1) Dezimalbr%C3%BCche_in_der_Stellenwerttafel|1) Dezimalbrüche in der Stellenwerttafel]] | ||
| Zeile 15: | Zeile 19: | ||
}} | }} | ||
== 4 Periodische Dezimalbrüche == | |||
Du hast zwei Möglichkeiten kennengelernt, einen Bruch in einen Dezimalbruch umzuwandeln: | Du hast zwei Möglichkeiten kennengelernt, einen Bruch in einen Dezimalbruch umzuwandeln: | ||
| Zeile 55: | Zeile 60: | ||
e) <math>{10 \over 7}</math> (nur für Profis) | e) <math>{10 \over 7}</math> (nur für Profis) | ||
{{Lösung versteckt|[[Datei:Zehn Siebtel umwandeln.png|mini|center]]|Lösung|Verbergen}} | {{Lösung versteckt|[[Datei:Zehn Siebtel umwandeln.png|mini|center]]|Lösung|Verbergen}} | ||
{{#ev:youtube|hqutjv1LAMU|800|start=443}} | |||
{{Box|Übung 2 (Buch)|Löse im Buch. Vergleiche deine Lösungen, achte vor allem auf die richtige Schreibweise! | |||
* S. 114, Nr. 12 d| Üben}} | |||
Aktuelle Version vom 20. März 2025, 03:40 Uhr
Startseite - Vorwissen
1) Dezimalbrüche in der Stellenwerttafel
2) Dezimalbrüchen in Brüche umwandeln
3) Brüche in Dezimalbrüche umwandeln
5) Dezimalbrüche am Zahlenstrahl eintragen
4 Periodische Dezimalbrüche
Du hast zwei Möglichkeiten kennengelernt, einen Bruch in einen Dezimalbruch umzuwandeln:
1. Möglichkeit: Umwandeln durch Erweitern bzw. Kürzen.
2. Möglichkeit: Umwandeln durch (schriftliche) Division.
Der Rest 1 wiederholt sich, also wiederholt sich im Ergebnis auch die Ziffer 3.
Beispiele:
a)
b)
c)
d)
e) (nur für Profis)